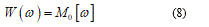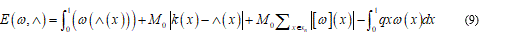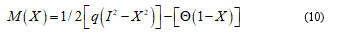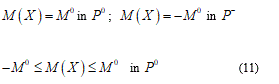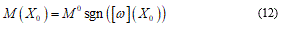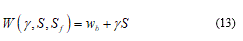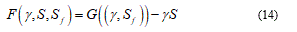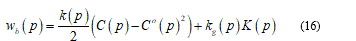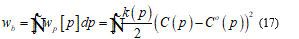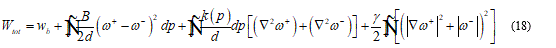A new approach modeling the fails in biological tissue is here proposed. Under the assumption that the cell membrane may be modeled, similarly as neo-Hookean materials, I develop the problem in the framework of nonlinear elasticity. I try to model the ice nucleation phenomenon when freezing and thawing occurs in cellular cryo-preservation. The generated surface of the ice seed can be either soft or wrinkled and, in the latter case a punch contact against the cell membrane take place. Restricting the attention on rescaled mono-dimensional sub-set, we extend the structured deformations theory by Del Piero & Owen, in the proposed model. I find a particular solution in agree to the classical fracture models besides a response function in according to the stress and strain fields distribution in biological materials. Developing the paper in two parts, in this one take care of nonlinear elasticity and biomechanics fundamentals.
cell membrane, fracture energy, stress concentration, structured deformations
One remarkable question easily in cellular biomechanics is how do cells sense and respond to mechanical stresses applied over the cell surface. Despite ample evidence that mechanical forces and mechano-transduction are critical for many cell functions including growth, proliferation, protein synthesis and gene expression, the specific mechanisms of mechanical force transmission remaining elusive [1]. For instance, understanding the molecular basis for mechano-transduction requires knowledge of the magnitude and distribution of forces throughout the cell at the molecular scale. A variety of different methods have been used to mechanically stimulate a cell, and the cellular response is multifaceted and diverse [2]. Both continuum and microstructural approaches have been used to determine force distributions. In the case of a continuum model, the details of the microstructure are ignored, and the forces transmitted via the individual microstructural elements are described in terms of stresses and corresponding strains, each assumed to be averaged over a distance many times greater than the characteristic dimension of the microstructure. Continuum models have frequently been used to obtain an estimate of cell stiffness, generally characterized by a Young’s modulus or shear modulus, from experiments in which the cell is deformed by external force application. For vary studies, about cell integrity such models are also useful in determining the distribution of stresses to regions of the cell remote from the site of force application and, from that, the force levels acting within individual sub elements. Here we will turn out our interest towards the cell or cellular membrane damage and or fracture. The investigation of damage mechanism in cells is important in biology as well as in medicine. Particularly, cryopreservation and cryosurgery together whit diagnostic purposes, for the pathologist, are some of the fields where a good knowledge of the effects and mechanism having great significance. Again, biological metabolism in living cells dramatically diminishes at low temperature, and then permits the long-term preservation of living cells and tissues for a multitude of bio-medical applications. Biologically speaking, it’s of primary importance, in the cryobiology field, the events surrounding extra or intracellular ice formation during freezing of biological cells. There are two general mechanism of ice nucleation [3]: the first one, when homogeneous nucleation in which the ice phase must be initiated by water molecules combining together to form a cluster of molecules in the solid phase. The second one, when nucleation of the ice phase occurs on hetero-phase impurity and ice is said to form heterogeneous nucleation. However, in both cases it’s possible to verify the origin of a glassy phenomenon over the intracellular and extracellular solution. In fact the living cells can be damaged by the cryopreservation process itself. All of this can cause significant biomechanical damage (extra and intracellular) during warming of cells cryopreserved by freezing with consequent cellular death. In this work, I will present a novel method for the cellular stress analysis, which uses variational approach through direct and no-direct methods, to compute stresses as well as displacements within the cellular membrane in response to a small localized variable load. The complex heterogeneity of the question takes me to develop the argument in more parts in order to be able to treat them clearly as well as complete form. In this first part a framework to nonlinear elasticity other than biomechanics extensions was regarded, successively entering on damage and fracture field. After classic variational approach, bio membrane elasticity and structural deformation theory have been implemented, focusing analytically on more evident effects of the load conditions on the cell membrane under freezing conditions.
Through this paper we use the nonlinear elasticity framework to represents the mechanical response of the biological cell constituents. Here we consider the materials as hyperelastic governed by constitutive law, linking the Piola-Kirchhoff Tk stress tensor and Cauchy-Green right strain tensor C=F TF and for this explanation we referring to Antman [4] and Taber [5]. We define W as the strain density potential and the hyperelasticity property involved in the relation:
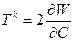 (1)
(1)
Here F is the deformation gradient defined as 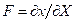 . In the isotropic case W = W(C) and so the strain potential depends only by the C invariants named W = W( IC, IIC, IIIC). Under the assumption of the incompressibility that is, J = det; F = 1, the dependence becomes only among two invariants and then, IC = IB, IIC = IIB, where B is the Cauchy-Green left strain tensor B = FF T. The follow constitutive law appears in Cauchy stress tensor terms:
. In the isotropic case W = W(C) and so the strain potential depends only by the C invariants named W = W( IC, IIC, IIIC). Under the assumption of the incompressibility that is, J = det; F = 1, the dependence becomes only among two invariants and then, IC = IB, IIC = IIB, where B is the Cauchy-Green left strain tensor B = FF T. The follow constitutive law appears in Cauchy stress tensor terms:
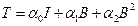 (2)
(2)
where the scalar coefficients ái = ái (Ii)i=0,1,2 were defined as material response functions, while I represent the identity tensor. The equation (2) can be specialized on different materials sets, particularly, as in the neo-Hookean type:
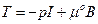 (3)
(3)
The next modification of the equation (3) offers the constitutive equation for biological tissues:
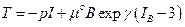 (4)
(4)
As clearly showed in the classic literature, [6] and [7], now it’s possible to characterize the answer of the biological tissues in energy terms. Many proposals have been developed to the energy forms starting from neo-Hookean, Mooney-Rivlin types or in poly-convex form. Here I will require a general form to the bio-tissue energy since the next proposed theoretical model is qualitative.
In this section our aim is explain the cellular membrane behavior when subjected to high deformation values. To show with a greater clarify I start with the classic assumptions in stress diffusion, damaging, fracture and then specializing in the bio-mechanical case. Here the significant aim is to investigate the mechanical response of frozen biological tissues to external compressive load done by ice crystals. In fact the mechanical interaction among ice-needles and cell membrane also enhances the destruction during the phase transition processes, causing localized mechanical stresses on the boundary cell. In other words these mechanical stresses are acting as a destruction mechanism causing permanents deformations and cracking in the bio tissues. Again damage in cell membranes appears after the mechanical stresses to contraction of the frozen tissue. A large literature has been developed over this field and only some reference were recalled as [8,9] and particularly in the paper [10] were showed some experimental results about the cellular membrane damaging. Now, in this time a fundamental claim will be placed, namely: what is the mechanical response in the biological materials under stress? These considerations to the purpose to specify the background hypothesis, such that to model the phenomenon. According to Gao [11] likely to the biopolymers behavior, the cellular membrane answer represents a local fast re-distribution; a slow before of a re-arrangement when undergo to the long-range interaction. So, it’s possible a stress map hypothesis with different zones around the high concentration stressed area (or fracture surface). Near this last I find a surrounding viscous dissipation zone (even damage area) and on the outside, a fully relaxed zones. After these evaluations, becomes obliged to deepen the mechanical questions explained in the following paragraphs.
In according to Villaggio [12,13] the more meaningful results in elasticity depend by the bounded domains hypothesis. However in many problems, size and configuration forms are such that the unbounded configuration becomes an easy way to resolve the problem. Now, in this case and roughly speaking I need to a configuration likely to the Flamant’s problem, under the natural restraint as the Lame’s modules, other than Toupin and Knowles theorems validity [12,14]. Consequently when I will find a solution, about the stress state produced by concentrate load acting on the boundary of an elastic half-plane I discovered just only stress component different to zero. So, the radial stress value expresses the fact that the concentrated load produces only radial stresses. On this consideration from now start the analysis of the laws stress propagation when a contact among two different bodies appears. In other words, considering the biomechanical problem in evaluation, without loss generality I will study an equivalent elastic-static problem, as a punctual load acting perpendicular on a curved surface. All the previous consideration allows making a suitable analytical model. In other words, to arrange stress and strain fields after the ice-needle cellular membrane contact. Figure 1 showing the real situation and address how to model the contact neighborhood.
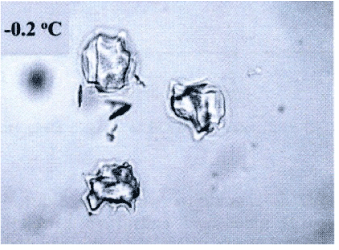
Figure 1. Ice sharp surface after freezing (from [14]).
Considering an opportune polar coordinates reference (r, q, j) where the ice load p is acting over the origin towards the half-space y ³ 0 then, the classical approach, after some calculations, takes the stress components:
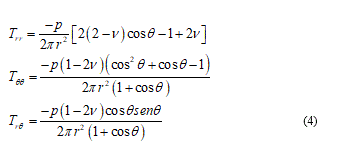
So, with this procedure only few cases can be easily showed as inclusive to the singularity effects which damage and, particularly, fracture. From comparison and confirm, to the experimental cell mechanics we referring to [15]. Generally, when the membrane curvature changes I need to introduce a singular solution in addition to equations (4) to adequate the resolution problem, but these additions are involving in a very analytical complication admitting long as well as laborious closed form solutions. To slenderize the problem is necessary a better physical specification and in the next I will be able for this. From mechanical point of view I can reduce the problem focusing it in the contact point among the punch load and the membrane surface. So that I find the classical solution describing the balanced configuration of a planar membrane subject to a given concentrate in-plane load other than, a given displacement field over the boundary. Under these assumptions the natural way to formulate the equilibrium problem is to look for the configuration minimizing the strain energy functional:

where k represents the membrane bending stiffness and u is the displacement field. The variational problem (5) can be reduced to the abstract form:
to find uÎ subset 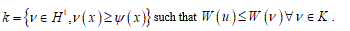
If functional W is convex and the subset K is a convex-cone the problem admits only a unique solution [16]. But even if this approach seems decisive, unfortunately consistent difficulties are emerging. Specifically, some restraints about the convex claim the deformation energy other the missing of the fracture energy. Consequently, the classical approach into the finite elasticity framework appears as very inadequate to this step and press to find a different approach.
Description of fracture or damage processes by means of continuum models has attracted great interest in different fields of engineering, mathematics, materials and no last even in biology and biomechanics. Here is necessary to do a fundamental consideration in order to ensure optimized strength and toughness of bio-membrane structure. Fracture of bio-solids involves breaking of atomic bonds, which is an intensively nonlinear process. In order to model failure mechanism in bio-solids in different size, I observe that multi-scales energies are necessary. In other words, the micro-scale cohesive force, jump to the deformation energy density at macro-scale.
Consequently, to model any material soft-body under stress, I need of general as detailed relationship or, roughly speaking, I need to represent, contemporarily, the configuration body as unfractured and fractured. So, considering the bio-medium as joined by cohesive force, when the cracks are distributed, the constitutive equations usually present it a strain softening branch, which approaches the zero stress value when crack has fully developed. All this, generally, involve in a problem of no-convex minimization and so the direct method in calculus of variation fails. Relatively to overcome this difficulty common tools consist to complete the continuum problem with particular conditions. In fact, the strain localization is zero in opportune sets. From a mathematical point of view, the variational approach specializes the join among the bulk energy W = W(C) with a cohesive fracture energy, function of the displacement discontinuity. In this way on the Ω body, the variational problem holds in the form:
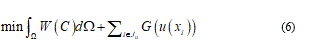
where Ju denotes the set of discontinuity points of u and u(xi) represents the jump of u at xi.
Structured deformations, introduced and developed by Del Piero & Owen [17-19], provide a natural way to describe not only the smooth deformations of classical solids other than the piecewise smooth deformations of fracture, but also more complex combinations of macroscopic and microscopic changes. Setting the problem on the SBV-space (special functions of bounded variation) [16], to as notorious from elasticity theory, the class of simple deformations is adequate to describe macroscopic fracture located on opportune singular surfaces. Adjusting some sequence of simple deformations, it becomes possible to model diffuse fractures throughout the body. A structured deformation can be identified by a pair
(g, G)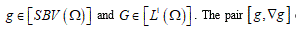 corresponds to simple deformations without microstructure and the difference
corresponds to simple deformations without microstructure and the difference 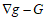 represents simple deformations due to microscopic rearrangements. Any structured deformations can be approximated by simple deformations
represents simple deformations due to microscopic rearrangements. Any structured deformations can be approximated by simple deformations 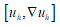 so that the sequence
so that the sequence 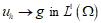 . Criterion to try both an effective energy and an approximate sequence is given by the minimization of:
. Criterion to try both an effective energy and an approximate sequence is given by the minimization of:
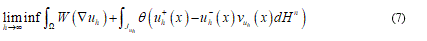
The formula (7) asserts the condition of the total energy minimization, representing it the elastic part (simple deformation) coexisting with fractured parts (jump set).
To fit structured deformation theory (SDT) at ours question I consider one opportune membrane strips undergoing at ice punch contact. Without loss generality I suppose the strip as clamped both left and right edge. The strip has high flexural deformations and following the previous assertions it’s possible suppose the moment – curvature diagram as in Figure 2. Supposing u as vertical displacement and ù the rotation among two sections of the membrane strip then follow the relation 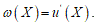 . Under the clamped boundary conditions u and u’ equals to zero in both edges. Now applying SDT I introduce the pair
. Under the clamped boundary conditions u and u’ equals to zero in both edges. Now applying SDT I introduce the pair 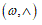 where L represents the elastic part of the curvature
where L represents the elastic part of the curvature 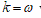 while the difference
while the difference 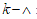 represents the plastic part. Performing an energetic approach:
represents the plastic part. Performing an energetic approach:
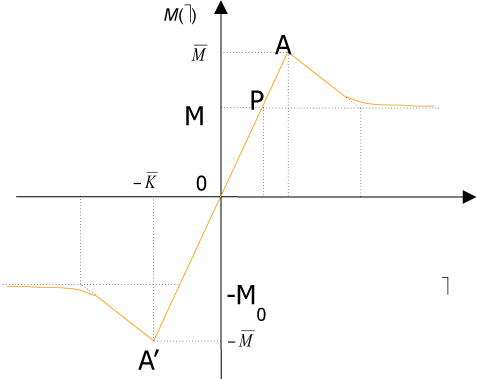
Figure 2. Constitutive law M vs ω.
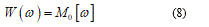
The equation (8) represents the associate deformation energy when the rotation w value is over a jump [ω]. Recalling equation (6), in this case, we have the total energy functional in the form:
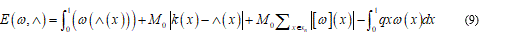
Here q(x) represents the external dead load and Sn the singular surface inner to the body.
The expression (9) should be minimized over the boundary conditions and after this the equilibrium equation follows:
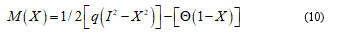
Now I consider e and d as some general perturbation over the equation (9) and P+, P- and P0 parts where the plastic deformation assume positive, negative and zero values. Developing (9) and omitting brief calculations I find:
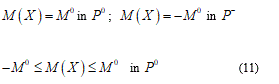
The position (11) tells us about the absence of the finite plastic zone. Vice versa in the elastic general perturbation:
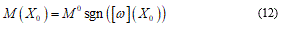
Namely, when the rotation w jump, it takes only one value among M0 or - M0 in fact likewise as a formed plastic hinge (Figure 3).
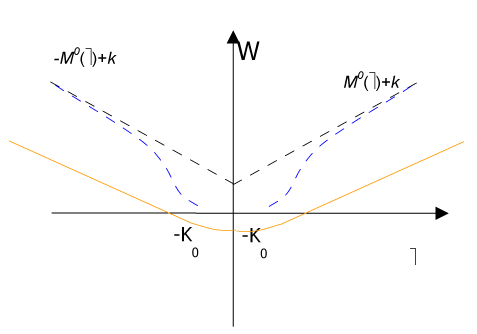
Figure 3. . Strain energy W(ω) diagram.
According to Agrawal & Steigmann [20] cell membranes may be regarded as two-dimensional solid likewise as liquid crystal. Again a cell membrane may be regarded as composite materials consisting of lipid bilayer, membrane cytoskeleton and protein [21], but the elastic properties of lipid bilayers oblige us to recognize Helfrich paper as theory point of departure [22]. Here I will be able to focus the attention on a bi-dimensional model with bending effects but neglecting the stretching mode. A similarly approach is followed by Steigmann [23] where wrinkling pattern in stretched sheets has been analyzed, deriving this from non-linear elasticity theory. In the proposed building model I will refer about the fundamental consideration on static equilibrium configuration of a red blood cell. For this I look as the base references Fung [6], Jenkins [24] and Maleki et al. [25] even if all theirs are not exhaustive but enough clear on the argument.
From now, I make an opportune framework on physics of cell bio-membranes, particularly on the cell boundary. Membranes define the boundaries of cells among internal and external components. They are essentially two-dimensional incompressible fluids with a molecular thickness that imparts bending elasticity. Here become evident obvious a clear differentiation about the loads conditions over the membrane. Considering the mechanical pulling case (i.e. ice seed action) and assuming conjugate variable the thickness. In this case I define as ó the mechanical stress on the surface S. Vice versa when I consider protein adsorption case the relevant variable become the fluctuating surface Sf. Then it’s possible to join two conjugate thermodynamic variables respectively: ó to S and ã to Sf where ã is the surface tension. From the energy balance:
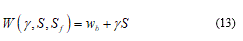
The last equation depends hardly from both exact values of g and S, while wb is the membrane elastic energy or better, the bending energy. Considering for instance an isolated membrane set (S,s) after some transformation of (13) I find the notable relation: [26]
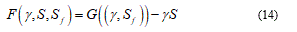
Achieving the main equation:

From now I will consider only the energy bending part wb and so I can extend the thin shell theory over the membrane. Recalling Helfrich [22] I get the energy form as:
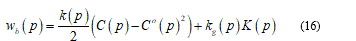
Here, the left term represent the local energy density, 𝐶 and 𝐶° the mean curvature, 𝑝 the surface position, (𝑝) the bending stiffness, 𝑘ℊ a microscopic parameter and 𝐾(𝑝) the Gaussian mean curvature. Neglecting thermal fluctuations I find the total bending energy on the whole surface.
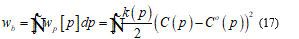
Under the continuum hypothesis, considering the bilayer as an elastic plate, the membrane stiffness may be considered as directly proportional to the cube of the thickness. To shorten on the question, I will set some fundamental consideration such that the following model may be implemented in a complete and clear way. For this I assume that in the model is present a neutral surface without stress so, I have an upper part, of the bilayer, as stretched and the lower parts, in contact with ice seed, as compressed. Then the total energy functional takes the form:
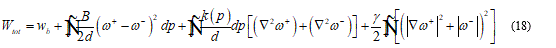
In the last formula d represent the membrane thickness, while ⍵+ and ⍵- the rotation jump. The functional (18) may be minimized under appropriate boundary condition on the both sides of the contact region.
The previous formula (18) appears as the completion of this first part since in this last equation has been deducted the elastic parts and the rotations jump parts. All this seem enough coherent with STD framework but in the future latter part I can develop the minimization problem thorough a global model containing all the properties showed in this parts and then eventually in a third part to finalize the numerical model.
- Deng L, Fairbank NJ, Fabry B, Smith PG, Maksym GN (2004) Localized mechanical stress induced time-dependent actin cytoskeletal remodelling and stiffening in culture airway smooth muscle cells. Am J Physiol Cell Physiol 287: 440-448. [Crossref]
- Huang H, Kamm RD, Lee RT (2004) Cell mechanics and mechanotransduction: pathways, probes, and physiology. Am J Physiol Cell Physiol 287: C1-11. [Crossref]
- Toner M, Cravalho EG, Karel M (1990 Thermodynamic and kinetics of intracellular ice formation during freezing of biological cells. Journal Applied Physics 67: 1582-1593.
- Antman SS (2005) Nonlinear Problems of Elasticity. (2ndedn), Springer.
- Taber LA (2004) Nonlinear Theory of Elasticity. World Scientific Publishing
- Woo SL (2004) Contribution of biomechanics to clinical practice in orthopaedics. Conf Proc IEEE Eng Med Biol Soc 7: 5455. [Crossref]
- Cowin SC, Doty SB (2007) Tissue Mechanics. Springer N.Y.
- Karlsson JOM, Cravalho EG (1994) A model of diffusion-limited ice growth inside biological cells during freezing. Journal Applied Physics 75: 4442-4455.
- Rabin Y, Olson P, Taylor MJ, Steif PS, Julian TB, et al (1997): Gross damage accumulation in frozen rabbit liver due to mechanical stress at cryogenic temperatures. Cryobiology 34: 394-405. [Crossref]
- Muldrew K, McGann LE (1990) Mechanisms of intracellular ice formation. Biophys J 57: 525-532. [Crossref]
- Ji B, Gao H (2004) Mechanical properties of nanostructures of biological materials. Journal of the Mechanics and Physics of Solids 52: 1963-1990.
- Villaggio P (1977) Qualitative Methods in Elasticity, Noordhoff Int. Publishing, Leyden.
- Villaggio P (1997) Mathematical Models for Elastic Structures, Cambridge University Press, N.Y.
- Mazur P, Pinn IL, Kleinhans FW (2007): Intracellular ice formation in mouse oocytes subjected to interrupted rapid cooling. Cryobiology 55: 158-166. [Crossref]
- Hu S, Chen J, Fabry B, Numaguchi Y, Gouldstone A, et al (2003) Intracellular stress tomography reveals stress focusing and structural anisotropy in cytoskeleton of living cells. Am J Physiol Cell Physiol 285: 1082-1090. [Crossref]
- Ambrosio L, Fusco N, Pallara D (2000) Functions of Bounded Variation and Free Discontinuity Problems, Clarendon Press Oxford.
- Del Piero G, Owen DR (1993) Structured deformations of continua. Archive for Rational Mechanics and Analysis 124: 99-155.
- Del Piero G (2001) On the energy of a structured deformations. Mathematics and Mechanics of Solids 6: 387-408.
- Del Piero G, Owen DR, Eds (2004) Foundations of the theory of structured deformations. CISM Course and Lecture 447 Springer.
- Agrawal A, Steigmann D (2008) Coexistent fluid-phase equilibria in biomembranes with bending elasticity. Journal of Elasticity 93: 63-80
- Tu ZC, An R, Ou-Yang ZC (2005) Elasticities and stabilities: lipid membranes vs cell membranes.
- Helfrich W (1973) Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforsch C 28: 693-703. [Crossref]
- Steigmann DJ (2013) A well-posed finite strain model for thin elastic sheets with bending stiffness, Mathematics and Mechanics of Solids 18: 103-112.
- Jenkins JT (1977) Static equilibrium configurations of a model red blood cell. J Math Biol 4: 149-169. [Crossref]
- Maleki M, Seguin B, Fried E (2013) Kinetics, materials symmetry, and energy densities for lipid bilayers with spontaneous curvature. Biomech Model Mechanobiol 12: 997-1017. [Crossref]
- Chou T (2002) Physics of cellular biomembranes. Lecture 3-Notes MATH-201 Dep. Mathematics UCLA Los Angeles.

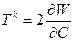 (1)
(1)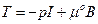 (3)
(3)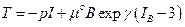 (4)
(4)
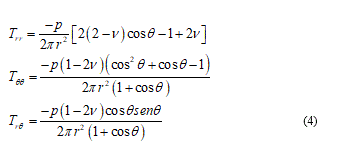

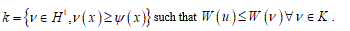
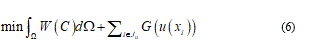
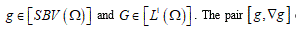 corresponds to simple deformations without microstructure and the difference
corresponds to simple deformations without microstructure and the difference 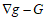 represents simple deformations due to microscopic rearrangements. Any structured deformations can be approximated by simple deformations
represents simple deformations due to microscopic rearrangements. Any structured deformations can be approximated by simple deformations 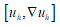 so that the sequence
so that the sequence 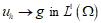 . Criterion to try both an effective energy and an approximate sequence is given by the minimization of:
. Criterion to try both an effective energy and an approximate sequence is given by the minimization of: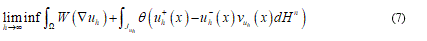
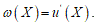 . Under the clamped boundary conditions u and u’ equals to zero in both edges. Now applying SDT I introduce the pair
. Under the clamped boundary conditions u and u’ equals to zero in both edges. Now applying SDT I introduce the pair 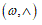 where L represents the elastic part of the curvature
where L represents the elastic part of the curvature 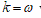 while the difference
while the difference 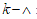 represents the plastic part. Performing an energetic approach:
represents the plastic part. Performing an energetic approach: