This paper develops a novel automated image processing algorithm of standard retinal ocular coherence tomography (SD-OCT), that allows for an objective investigation of age-related retinal changes in normal subjects, based on automated quantitative reflectivity changes. A database of SD-OCT retinal scans (Zeiss Cirrus HD-OCT 5000) was prospectively established from 200 normal subjects without clinical evidence of retinal pathology. A novel segmentation algorithm was applied to extract retinal layers and normalize the reflectivity range, utilizing a novel normalized reflectivity scale (NRS) ranging from 0 units (vitreous) to 1000 units (retinal pigment epithelium [RPE]). NRS decreased with age overall, with the greatest declines seen in the ellipsoid zone (3.91 ± 2.11 NRS · yr−1,F1,322 = 100.9;p < 0.0001), and NFL (3.84 ± 1.72 NRS · yr−1,F1,322 = 112.6;p < 0.0001). Normal aging had little to no effect on the reflectivity of RPE or ELM. It was possible to report the reflectivity changes in the retina that occur in normal aging subjects. This novel algorithm shows promise of early detection of occult retinal pathology otherwise undetectable.
spectral domain optical coherence tomography (SD-OCT), human retina, reflectivity, normalized reflectivity scale (NRS), retina segmentation, aging
Spectral domain optical coherence tomography (SD-OCT) is a widely used tool in the evaluation and management of most retinal conditions [1-3]. Utilizing interferometry, low coherence light is reflected from retinal tissue to produce a two-dimensional grayscale image of 5 the retinal layers. Differences in reflectivity of retinal layers produce different intensities on SD-OCT scan, allowing for noninvasive imaging of the retinal layers [1-4]. This detailed crosssectional anatomy of the retina is often referred to as in-vivo histology and is instrumental in the assessment of most retinal conditions including diabetic retinopathy (DR), age-related macular degeneration (AMD), macular hole, macular edema, vitreo-macular traction (VMT),10 choroidal neovascularization, and epiretinal membrane. SD-OCT can be also used to assess retinal nerve fiber layer (RNFL) thickness for the evaluation of glaucoma5. Retinal layer morphology and retinal thickness measurements are used to identify and measure retinal abnormalities such as macular edema, and these measurements are also used to monitor disease progression and response to treatment [1-3]. With the exception of retinal thickness 15 measurements, current SD-OCT provides limited objective quantitative data, and therefore images must be subjectively interpreted by an eye specialist [1]. As a result, interpretation of SD-OCT is susceptible to human bias and error. Ideally, OCT data should be tracked quantitatively and objectively in order to monitor the progression of abnormalities as well as aid in the diagnosis of various pathologies. The purpose of this study was to develop a 20 novel automated algorithm that objectively quantifies reflectivity of retinal layers from OCT images, and to apply this algorithm for the investigation of subtle changes that occur in the normal retina with age.
The proposed method consists of three basic steps:
- Aligning the input image to the shape database constructed from different images.
- Applying the joint model to the aligned image.
- Obtaining the final segmentation.
The mathematical details of the proposed joint model are detailed below.
Data collection
This study was reviewed and approved by the Institutional Review Board (IRB) at the University of Louisville - School of Medicine. Following IRB approval, subjects were recruited at the Kentucky Lions Eye Center, University of Louisville Department of Ophthalmology and Visual Sciences, Louisville, Kentucky between June 2015 and December 2015. Informed consent was obtained from all participants. Subjects with normal retinas ranging in age 35 from 10 to 79 years old were included in the study. Past medical history, ophthalmologic history, smoking status, and current medications were obtained via chart review and subject interview. Persons with history significant for any retinal pathology, history significant for diabetes mellitus, high myopia defined as a refractive error greater than or equal to -6.0 diopters, and tilted OCT image were not included in this study. A database of SD-OCT 40 scans was prospectively established from 200 normal subjects using the Zeiss Cirrus HD-
OCT 5000. SD-OCT data were exported for analysis as 8-bit, greyscale raw files with size 1024 pixels 1024 pixels N slices, where N = 5 or 21. For N = 5, the field of view as 6 mm nasal-temporal (N-T) and 2 mm posterior-anterior (P-A), and the slice spacing was 0.25 mm. For N = 21, the field of view was 9 mm N-T and 2 mm P-A, while the slice spacing 45 was 0.3 mm.
Automatic segmentation of twelve retinal layers
let 
denote a grayscale image and an associated region map on a finite arithmetic lattice R2 and with values from finite sets Q and L of integer intensities and region labels, respectively. An input OCT image, g, co-aligned to the training database, and its map, m, are described with a joint probability model [6]:
P(g,m) = P(g|m)P(m) (1)
combining a conditional distribution of the images given the map P(g|m), and an unconditional probability distribution of maps P(m) = Psp(m)PV(m). Here, Psp(m) denotes a weighted shape prior, and PV(m) is a Gibbs probability distribution with potentials V, that 55 specifies a second-order MGRF model of spatially homogeneous maps m.
Adaptive shape model Psp(m)
The shape prior is constructed using several training OCT scans (6 male and 6 female images in our experiments below), selected to capture biological variability of the whole data set. Their ground truth” region maps were delineated under supervision of retina specialists. Using one of the optimal scans as a reference (no tilt, centrally located fovea), the others were co-registered using a thin plate spline (TPS) [7]. The shape prior is defined as:
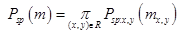 (2)
(2)
where Psp(m)
denotes the weighted shape prior, psp:x,y(m) is the pixel-wise probability for label m, and (x,y) is the image pixel with gray level g. The same deformations were applied to their respective ground truth segmentations, which were then averaged to produce a probabilistic shape prior of the typical retina, i.e., each position (x,y) in the reference space is assigned a prior probability P(m) to lie within each of the 12 tissue classes. An image to be segmented is first aligned to the shape database by a new technique integrating the TPS with multi-resolution edge tracking that identifies control points to
initialize the alignment. First, “a` trous” algorithm [8] decomposes each scan by undecimated 130 wavelet transform. In a three-band appearance of the retina, two hyperreflective bands are separated by a hyporeflective band, corresponding roughly to the layers from ONL to MZ (Figure 1). Contours following the gradient maxima of this wavelet component provided initial estimates of the vitreous/NFL, MZ/EZ, and RPE/choroid boundaries (Figure 3). The fourth gradient maximum could estimate the OPL/ONL boundary, but that is not sharp enough 70 an edge to be of use. These ridges in gradient magnitude were followed through scale space to the third wavelet component, corresponding to a scale of approximately 15 micrometers for the OCT scans used in this study.

Figure 1. A typical OCT scan of a normal subject showing the 12-distinct layers.

Figure 2. Illustration of the basic steps of the proposed OCT segmentation framework.
The foveal peak is identified as the closest point between the vitreous/NFL and MZ/EZ contours. Then control 135 points are located on these boundaries at the foveal peak and at 75 uniform intervals from it. Finally, the optimized TPS aligns the input image to the shape database using these control points, so that the shape prior can be used to segment the aligned image.
First-order intensity model P(g|m)
To account for visual appearance of the input image, its empirical marginal probability distribution of intensities is closely approximated with a linear combination of sign-alternate discrete Gaussians (LCDG) and separated into individual components (also LCDGs) for different regions, associated each with a dominant mode. This model and its ExpectationMaximization-based learning are detailed in [9]:
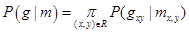 (3)
(3)
where m takes one of the labels from 1 to 12.
Second-order MGRF model PV(m)
For better spatial homogeneity of segmentation, the MGRF model of dependencies be-tween adjacent region labels is combined with the shape prior and intensity model [9]:
 (4)
(4)
where bi-valued Gibbs potentials V = (V (k,k’) : k,k’ ∈ L) for the nearest 8-neighborhood when νs = {(1,0),(−1,1),(0,1),(1,1)}, depend on equality of each nearest pair of labels: V (k,k’) = γ ≥ 0 if k = k’ and −γ otherwise. The potentials are approximated analytically from the empirical probability of equal label pairs in the training region maps.
The steps of the segmentation framework are illustrated in Figure 2 whereas Figure 5 shows segmentation results on different SD-OCT images from subjects in different decades of life. The performance of the proposed segmentation framework relative to manual segmentation was evaluated using the agreement coefficient (AC) and the Dice similarity coefficient of similarity (DSC) [10,11].

Figure 3. Illustration of wavelet decomposition for an OCT image (A), highlighting the large scale structure of the retina in (B). Multiscale edges shown in (C) near the foveal peak, inside the bounded region of (A). At the finest level of detail, three boundaries are detected (D).

Figure 4. The segmentation steps: (a) an OCT image of a 65 year-old female, (b) edge tracking with wavelet decomposition, (c) co-alignment using TPS control points, (d) LCDG-modes for different layers, (e) segmentation after using the joint MGRF model, and (f) overlaid layers edges on the original image.

Figure 5. Segmentation results for different normal OCT images in row (A). Results of the proposed approach are displayed in row (B) and results of the approach13 are displayed in row (C). The DSC score is displayed above each result.
Quantitative data derived from SD-OCT images
Several quantitative data can be derived from the segmented SD-OCT images in order to optimally characterize retinal morphology. This paper specifically addresses and discusses the reflectivity measurements that were obtained from two regions per scan, comprising the thickest portions of the retina on the nasal and temporal sides of the foveal peak.
Mean reflectivity is expressed on a normalized scale, calibrated such that the formed vitreous has a mean value of 0 NRS, and the retinal pigment epithelium has a mean value of 1000 NRS. The average grey level within a segment was calculated using Hubers M-estimate, which is resistant to outlying values that may be present, such as very bright pixels in the innermost segment that properly belong to the internal limiting membrane and not the NFL.
Average grey levels were converted to NRS units via an offset and uniform scaling. Statistical analysis employed ANCOVA [12] on a full factorial design with factors gender, side of the fovea (nasal or temporal) and retinal layer, and continuous covariate age.
Validation of the proposed approach
Reliability of our technique was assessed using repeated scans of eight healthy individuals (7 males, 1 female), which were done for this purpose and not part of the aging study. Two scans were obtained from each eye. The OCT device was repositioned and refocused on every scan. Measurements of retina layer thickness and reflectivity were used to quantify the reliability of segmentation and the normalized reflectivity scale. Reliability analysis employed mixed effects analysis of variance with a fixed constant term and random effects for individual subject, lateral position across macula (from 2.5 mm temporal to 2.5 mm nasal), and retina layer. From the variance component S2, the intra-class correlation (ICC)
was used as the reliability metric:
S2layer
 (5)
(5)
Slayer
This section addresses the experimental results after applying the proposed segmentation approach on the images collected, followed by analysis of the reflectivity measure across the different decades of life. The proposed novel segmentation approach was first validated using ground truth for subjects, which was collected from 200 subjects aged 10–79 years. Subjects with high myopia (≤ −6.0 diopters), and tilted OCT were excluded. This ground truth was created by manual delineations of retina layers reviewed with different retina specialists (SS,AP, AH, DS).
Step-by-step demonstration to show the ability of the proposed segmentation approach for a normal subject is shown in Figure 4. First, the edges of the input OCT image (Figure 4(a)) is tracked using wavelet decomposition method (Figure 4(b)) and is followed by its co-alignment to the shape database using identified TPS control points (Figure 4(c)). Initial segmentation result is first obtained using the shape model (Figure 4(d)) then refined using the joint-MGRF model to obtain the final segmentation result (Figure 4(e)). More segmentation results for normal subjects are demonstrated in Figure 5. The robustness and accuracy of our approach are evaluated using both AC and DSC metrics, and the AD distance metric comparing our segmentation with the ground truth. Comparison with 200 manually segmented scans found the mean boundary error was 6.87 micrometers, averaged across all 13 boundaries; the inner (vitreous) boundary of the retina was place most accurately, with 2.78 micrometers mean error. The worst performance was on the outer (choroid) boundary, with mean deviation of 11.6 micrometers from ground truth. The AC gives mean of 77.2% with standard deviation
4.46% (robust range 64.0%86%). Some layers were more accurately automatically segmented than others (Figure 5), with Dice coefficient of similarity as high as 87.8% with standard deviation of 3.6% in the outer nuclear layer (robust range 79.2%95.1%) but low as 58.3% with standard deviation of 13.1% in the external limiting membrane.
Additionally, the advantage of the proposed segmentation technique is highlighted by comparing its performance against graph theory based approach [10]. This approach produces mean boundary error 284 micrometers; only the RPE/choroid boundary was reliably detected, with mean error of 15.1 micrometers, standard deviation 8.6 micrometers. The AC was very law whereas the DSC mean 30.3% with (s.d. 0.358) in ONL–EZ (outer nuclear layer and inner segments of photoreceptors) and 40.7% with (s.d. 0.194) in OPR–RPE (hyperreflective complex). DSC mean zero elsewhere. Comparative segmentation results of our approach versus another one [13] for some selected data are shown in Figure 5. Table 1 summarizes the quantitative comparison of our segmentation method and the other method [13] versus the ground truth, based on the three evaluation metrics for all subjects. Statistical analysis using paired t-test demonstrates a significant difference in terms of all three metrics of our method over [13], as confirmed by p—values 150 < 0.05 (Table 1). This analysis clearly demonstrates the promise of the developed approach for the segmentation of the OCT scans.
Table 1. Comparative segmentation accuracy of the proposed segmentation and13 using (DSC), (AC), and (AD) metrics. Values are represented as mean ± standard deviation.
|
Evaluation Metric |
DSC |
AC,% |
AD, µm |
Our approach |
0.76 ± 0.16 |
73.2 ± 4.5 |
6.87 ± 2.8 |
Other 13 |
0.41 ± 0.263 |
2.25 ± 9.7 |
15.1 ± 8.6 |
2021 Copyright OAT. All rights reserv
p−value |
< 0.0001 |
< 0.0001 |
< 0.00395 |
After excluding low quality and tilted scans, reflectivity was measured in the right eye of 138 women and 62 men, between 10 and 76 years of age. The female subgroup was slightly older on average at 43.7 years compared to 37.6 years for the male subgroup (t106 = 1.91;p = 0.059).
Normalized reflectivity varied significantly with age (F1,4368 = 327;p < 0.0001), gender (F1,4368 = 5.11;p = 0.024), and layer (F11,4368 = 2330;p < 0.0001), but not side of the fovea (F1,4368 = 0.424;p = 0.515). The slope, or year to year change in NRS, varied significantly by retinal layer (F11,4368 = 14.77;p < 0.0001). The interactions of side of the fovea with layer was statistically significant (F11,4368 = 29.1;p < 0.0001). No other terms in the model were significant. The gender effect, while statistically significant, amounted to only 1.4 NRS (male ¿ female). NRS decreased with age overall (Figure 6), with the greatest declines seen in the ellipsoid zone (3.43 NRS/year), and NFL (3.50 NRS/year). Normal aging had little to no effect on the RPE (0.72 NRS/year).

Figure 6. Slopes showing the decline of the reflectivity for the twelve layers with age, along with their 95% confidence intervals.
Analysis of repeated scans from eight healthy individuals produced ICC estimates of 0.813 and 0.831 for retina layer thickness and normalized reflectivity, respectively. These values indicate “good” agreement between segmentation of different scans of the same eye, using the ICC cutoff values suggested by Indrayan [14].
170 Ophthalmic OCT, first introduced in 1991 by Huang et al. [4] practically revolutionized ophthalmic practice. SD-OCT is an essential part of the modern retinal evaluation, which provides invaluable and unsurpassed clinical information, otherwise unavailable. The basic SD-OCT image is a histology-equivalent optic reflectivity B-scan retinal section. To-date, all SD-OCT images are manually interpreted by an ophthalmologist on the basis of anatomic appearance and human pattern recognition. The need for an automated processing and an un-biased interpretation of retinal scans is pertinent. Accurate reproducible automated SD-OCT image analysis will enable earlier identification of retinal conditions, enable better follow up strategies and plans, eliminate human errors, and allow more efficient and cost-effective patient care. Although initial preliminary automated image processing exists in some commercially available SD-OCT models, it is currently limited to retinal thickness,
retinal volume and partial retinal segmentation.
Segmentation of retinal layers from SD-OCT images has been previously attempted by several groups. Several notable achievements and pitfalls are worth discussing. Ishikawa et al. [15] developed an automated algorithm that identifies four retinal layers using an adaptive thresholding technique. This algorithm failed with poor-quality images and also failed with some good-quality ones. Bagci et al. [16] proposed an automated algorithm that extracted seven retinal layers using a customized filter for edge enhancement in order to overcome uneven tissue reflectivity. However, further work is needed to apply this algorithm to more advanced retinal abnormalities. Mishra et al. [17] applied an optimization scheme to identify seven retinal layers. The algorithm could not separate highly reflective image features. Another automated approach was proposed by Rossant et al. [18] to segment eight retinal layers using active contours, k-means, and random Markov fields. This method performed well even when retinal blood vessels shaded the layers, but failed in blurry images. Kajic et al. [19] developed an automated approach to segment 8 layers using a large number of manually segmented images that were used as input to a statistical model. Supervised learning was performed by applying knowledge of the expected shapes of structures, their spatial relationships, and their textural appearances. Yang et al. [20] devised an approach to segment eight retinal layers using gradient information in dual scales, utilizing local and complementary global gradient information simultaneously. This algorithm showed promise in segmenting bothhealthy and diseased scans, yet more work is needed to evaluate it on retinas affected with outer/inner retinal diseases. Yaz et al. [21] presented a semi-automated approach to extract 9 layers from OCT images using Chan-Veses energy-minimizing active contour without edges model. This algorithm incorporated a shape prior based on expert anatomical knowledge of retinal layers. The proposed method required user initialization and was never tested on human retinas nor on diseased retinas. Ehnes et al. [22] developed a graph-based algorithm for retinal segmentation which could segment up to eleven layers in images of different devices. The algorithm yet worked only with high-contrast images. Kafieh et al. [23] also used graphbased diffusion maps to segment the intraretinal layers in OCT scans from normal controls and glaucoma patients. Chui et al. [13] proposed an automated approach for segmenting 7 retinal layers using graph theory along with dynamic programming, this method accurately segments eight retinal layer boundaries in normal adult eyes more closely to an expert grader which reduced processing time. Rathke et al. [24] proposed a probabilistic approach that models the global shape variations of retinal layers along with their appearance using a variational method. Kaba et al. [25] also segmented 8 retinal layers, but using continuous maximum flow algorithm, that was followed by image flattening based on the detected upper boundary of the outer segment (OS) layer in order to extract the remaining layers boundaries. Srimathi et al. [26] applied an algorithm for retinal layer segmentation that first reduced speckle noise in OCT images, then extracted layers based on a method that combines active contour model and diffusion maps. Ghorbel et al. [27] proposed a method for segmenting 8 retinal layers based on active contours and Markov Random Field (MRF) model. A Kalman filter was also designed to model the approximate parallelism between photoreceptor segments. Dufour et al. [28] proposed an automatic graph-based multi-surface segmentation algorithm that added prior information from a learnt model by internally employing soft constraints.
Graph theory approach was also employed by Garvin et al. [29] for segmenting OCT retina layers, while incorporating varying feasibility constraints and true regional information. Tian et al. [30] proposed a real-time automated segmentation method that was implemented using the shortest path between two end nodes. This was incorporated with other techniques, such as masking and region refinement, in order to make use of the spatial information of adjacent frames. Yin et al. [31] applied a user-guided segmentation method that first manually defined lines at irregular regions for which automatic approached fail to segment. Then the algorithm is guided by these traced lines to trace the 3D retinal layers using edge detectors that are based on robust likelihood estimators.
The above discussion demonstrates that there are some limitations associated with retinal layers segmentation such as the low accuracy achieved when having images with low signal to noise ratio (SNR), and the fact that the majority of the proposed approaches could segment only up to eight retinal layers, while methods that segmented more layers were successful only with high-contrast images.
In order to overcome the aforementioned limitations, this paper proposes a novel algorithm to automatically segment 12 retinal layers (Figure 1), and analyze their reflectivity. It employs a hybrid segmentation model that combines intensity, spatial, and shape information. To the best of our knowledge this is the first study to demonstrate fully automated segmentation approach that has the ability to extract 12 layers at different decades of life, which allowed the detection of subtle changes that occur in the normal retina with aging.
The computerized automated data analysis revealed subtle but clinically significant quan-titative characteristics of retinal layer reflectivity and demonstrated significant changes throughout the decades of life and between genders. The novel automated algorithm provides additional quantitative measurements of SD-OCT images and revealed that the normal aging process results in significant changes in the reflectivity of the ellipsoid and nerve fiber layers. This adds to our understanding of the decline in visual function that occurs in normal human aging.
The retina, being a direct derivative of the brain, cannot heal and does not regenerate. To-date retinal diseases are detected after substantial anatomical damage to the retinal architecture has already occurred. Successful treatment nowadays can only slow disease progression, or at best preserve existing visual function. Revealing the normal topographic and age-dependent characteristics of retinal reflectivity and defining rates of normal agerelated changes, will enable us to detect pre-disease conditions. This carries the promise for the development of future preventive retinal medicine that will allow early detection and early treatment of retinal conditions prior to the recognition of advanced anatomy-distorting clinical findings that is available today.
- Jaffe GJ and Caprioli J (2004) Optical coherence tomography to detect and manage retinal disease and glaucoma. American Journal of Ophthalmology 137: 156–169.
- Baghaie Z Yu, Dsouza RM (2015) State-of-the-art in retinal optical coherence tomography image analysis. Quantitative Imaging in Medicine and Surgery 603.
- Sakata LM, DeLeon-Ortega J, Sakata V, Girkin CA (2009) Optical coherence tomography of the retina and optic nerve–a review. Clinical & Experimental Ophthalmology 1: 90–99.
- Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, et al. (1991) Optical coherence tomography Science (New York, NY) 5035: 1178.
- Gracitelli CP, Abe RY, Medeiros FA (2015) Spectral-domain optical coherence tomography for glaucoma diagnosis. The open Ophthalmology Journal.
- El-Baz A, Elnakib F, Khalifa MA, El-Ghar, P. McClure A, et al. (2012) Precise segmentation of 3-d magnetic resonance angiography. IEEE Transactions on Biomedical Engineering 7: 2019–2029.
- Lim J Yang MH (2005) A direct method for modeling non-rigid motion with thin plate spline in Computer Vision and Pattern Recognition. IEEE Computer Society Conference on, 1, IEEE 1196–1202.
- Lega E, Scholl H, Alimi JM, Bijaoui A, Bury P (1995) A parallel algorithm for structure detection based on wavelet and segmentation analysis Parallel Comput 2: 265–285.
- Alansary M, Ismail A, Soliman F, Khalifa M, Nitzken A, et al. (2015) Infant brain extraction in t1-weighted mr images using bet and refinement using lcdg and mgrf models, IEEE Journal of Biomedical and Health Informatics.
- Dice LR (1945) Measures of the amount of ecologic association between species. Ecology 3: 297–302.
- Gwet KL (2008) Computing inter-rater reliability and its variance in the presence of high agreement. British Journal of Mathematical and Statistical Psychology 1: 29–48.
- Lomax RG, Hahs-Vaughn DL (2013) Statistical concepts: A second course, Routledge.
- Chiu SJ, Li XT, Nicholas P, et al. (2010) Automatic segmentation of seven retinal layers in sdoct images congruent with expert manual segmentation. Optics express 19413–19428.
- Indrayan (2013) Clinical agreement in quantitative measurements in Methods of Clinical Epidemiology Springer 17–27.
- Ishikawa H, Stein DM, Wollstein G, Beaton S, Fujimoto JG, et al. (2005) Macular segmentation with optical coherence tomography,” Investigative Ophthalmology & Visual Science 6: 2012–2017.
- Bagci AM, Shahidi M, Ansari R, Blair M, Blair NP, et al. Thickness profiles of retinal layers by optical coherence tomography image segmentation. American Journal of Ophthalmology 5: 679–687.
- Mishra A, Wong A, Bizheva K, Clausi DA (2009) Intra-retinal layer segmentation in optical coherence tomography images. Opt Express 17: 23719-23728. [Crossref]
- Rossant F, Ghorbel I, Bloch M, Paques M, Tick S, et al. (2009) Automated segmentation of retinal layers in oct imaging and derived ophthalmic measures in 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro IEEE 1370–1373.
- Kaji´c V, Pova B, zay B, Hermann, et al. (2010) Robust segmentation of intraretinal layers in the normal human fovea using a novel statistical model based on texture and shape analysis Opt Express 14: 14730–14744.
- Yang Q1, Reisman CA, Wang Z, Fukuma Y, Hangai M, et al. (2010) Automated layer segmentation of macular OCT images using dual-scale gradient information. Opt Express 18: 21293-21307. [Crossref]
- Yazdanpanah G, Hamarneh BR, Smith E et al. (2011) Segmentation of intra-retinal layers from optical coherence tomography images using an active contour approach. Medical Imaging, IEEE Transactions.
- Ehnes Y, Wenner C, Friedburg, et al. (2014) Optical coherence tomography (oct) device independent intraretinal layer segmentation. Transl Vis Sci Technol.
- Kafieh R, Rabbani H, Abramoff MD, et al, (2013) Intra-retinal layer segmentation of 3D optical coherence tomography using coarse grained diffusion map. Med Image Anal 17: 907– 928.
- Rathke F, Schmidt S, Schn C (2014) Probabilistic intra-retinal layer segmentation in 3-d oct images using global shape regularization. Medical image analysis 5: 781–794.
- Kaba D, Wang Y, Wang C, Liu X, Zhu H, et al. (2015) Retina layer segmentation using kernel graph cuts and continuous max-flow. Opt Express 23: 7366-7384. [Crossref]
- Srimathi M, Usha A (2015) Retinal layer segmentation of optical coherence tomography images with active contour model and diffusion map. Australian Journal of Basic and Applied Sciences 15: 166–171.
- Ghorbel F, Rossant I, Bloch, et al. (2011) Automated segmentation of macular layers in oct images and quantitative evaluation of performances. Pattern Recognition 1590–1603.
- Dufour PA, Ceklic L, Abdillahi H, et al. (2013) Graph-based multi-surface segmentation of OCT data using trained hard and soft constraints. IEEE Trans. Med. Imaging 32: 531–543.
- Garvin MD, Abr`amoff, X Wu, et al. (2009) Automated 3-D intraretinal layer segmentation of macular spectral-domain optical coherence tomography images. IEEE Trans Med Imag 28 1436–1447.
- Tian J, Varga B, Somfai GM, Lee WH, Smiddy WE, et al. (2015) Real-Time Automatic Segmentation of Optical Coherence Tomography Volume Data of the Macular Region. PLoS One 10: e0133908. [Crossref]
- Yin X, Chao JR, Wang RK (2014) User-guided segmentation for volumetric retinal optical coherence tomography images. Journal of Biomedical Optics 19: 086020–086020.

 (4)
(4) (5)
(5)