Abstract
Light travels through a vacuum at speed c regardless of the motion of the light source or that of an observer's frame of reference. Consequently, some time is required for light to travel from a light source to an observer in space, such that the emission of light and the observance of the emitted light are not simultaneous. Based on these considerations, a method for measuring the absolute velocity of an observer is proposed, which could be used for determining a spacecraft's state of motion from inside a closed cabin. In this study, a new explanation of the Lorentz transformation is also introduced.
Key words
coordinate system, reference system, movement, absolute velocity, relativity, lorentz transformation, time, space, observer, light source
The following analysis presents a practical approach for measuring the absolute velocity of an observer, which could be used for determining a spacecraft's state of motion from inside a closed cabin. The concept of absolute velocity generally refers to a standard uniform velocity of the various objects of a physical system relative to a postulated immobile space that exists independently of the physical objects contained therein (i.e., an absolute space). Herein, we present an approach based on rigid kinematics to demonstrate that the absolute velocity of an observer can be determined from the fact that light travels through a vacuum at speed c regardless of the motion of the light source or that of an observer's frame of reference. Consequently, some time is required for light to travel from a light source to an observer in space, such that the emission of light and the observance of the emitted light are not simultaneous.
In the proposed analysis, we first provide the following conventions for the coordinate systems under consideration. We assume a Cartesian coordinate system comprised of three pair-wise perpendicular axes originating from point (0,0,0), where any point P in space can be defined by its coordinates along the x, y, and z axes, represented by an ordered pair of real numbers (x,y,z). An inertial reference system S is assumed to be represented by a space rectangular coordinate system (x,y,z) whose origin is O. A series of standard clocks (denoted as S clocks) are located at stationary points in S. The S clocks are mutually calibrated (i.e., they provide equivalent readings at the same instant in time) based on the transmission and reception of a light signal. Specifically, at time tA, a light beam is projected from clock A to clock B, which is then reflected at time tB by clock B back toward clock A, and arrives at clock A at time tA'. If 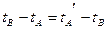 , the two clocks are calibrated. For any event located at coordinates x,y,z, its time coordinate t is given by the reading of the event-related S clock. Similarly, another inertial reference system S' is established based on a second space rectangular coordinate system (x',y',z') whose origin is O', and another series of mutually calibrated standard clocks (S' clocks) are located at stationary points in reference system S'. For any event located at coordinates x',y',z', its time coordinate t' is given by the reading of the event-related S' clock.
, the two clocks are calibrated. For any event located at coordinates x,y,z, its time coordinate t is given by the reading of the event-related S clock. Similarly, another inertial reference system S' is established based on a second space rectangular coordinate system (x',y',z') whose origin is O', and another series of mutually calibrated standard clocks (S' clocks) are located at stationary points in reference system S'. For any event located at coordinates x',y',z', its time coordinate t' is given by the reading of the event-related S' clock.
Because the respective origins of the spatial and temporal coordinates, as well as the directions of the coordinate axes can be selected arbitrarily to a large extent, the relationships between S and S' employed herein are based on the following conventions, which have been applied for simplicity.
(1) At a particular instant in time, the origins and coordinate axes of the two systems are superposed, and the clocks respectively located at O and O' are set to zero, i.e.,  .
.
(2) The x and x' axes are coincident in the direction of the relative motion of S and S'; thus, x and x' are coincident at all times, while y and y', as well as z and z' are parallel.
(3) S' moves along the +x direction of S.
The proposed analysis is based on the fundamental principle that light in a vacuum travels at a constant velocity c regardless of the motion of either the observer or the light source. Thus, we herein define the absolute velocity U of the observer, which is assumed to be linear and uniform, as 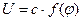 , where f(φ) represents a function of the geometrical relationship between the direction of a light signal and the direction of U, denoted herein as φ.
, where f(φ) represents a function of the geometrical relationship between the direction of a light signal and the direction of U, denoted herein as φ.
Two new explanations of the relativity of time and length are provided in the proposed analysis, which differ from Einstein's explanations (please refer to “On the Electrodynamics of Moving Bodies”). These explanations are introduced in the following sections.
The relativity of time
Owing to the finite velocity of light, some time is required for light to travel from a light source to an observer in space. It can therefore be deduced that the emission of light and the observance of light cannot be simultaneous. Based on the constancy of the velocity of light and the conditions illustrated in Figure 1, we define the following factors. The positions of a light source and an observer at 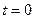 , at which time the light source emits light (denoted as event R), are given respectively as A and H0. During the period of light propagation from
, at which time the light source emits light (denoted as event R), are given respectively as A and H0. During the period of light propagation from 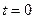 to
to 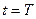 , the observer travels a distance U∙T from position H0 to H, whereupon the observer receives the emitted light. Accordingly, we define
, the observer travels a distance U∙T from position H0 to H, whereupon the observer receives the emitted light. Accordingly, we define 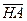 as the distance l between the position of the observer upon receiving the light signal at
as the distance l between the position of the observer upon receiving the light signal at 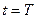 and the position of the light source when emitting light at
and the position of the light source when emitting light at 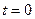 . Owing to the constancy of the velocity of light,
. Owing to the constancy of the velocity of light, 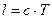 . The distance
. The distance 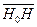 is equivalent to U∙T. Finally, we define
is equivalent to U∙T. Finally, we define 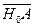 as the distance l0 between the position of the observer at
as the distance l0 between the position of the observer at 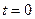 and the position of the light source at
and the position of the light source at 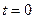 . Here, we introduce a consideration of the observer's position at
. Here, we introduce a consideration of the observer's position at 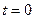 , which was previously thought to have no physical significance. If the states of motion of the observer and the light source are equivalent, l0 is given, such that U can be calculated via the triangular relations illustrated in [1,2],Figure 1.
, which was previously thought to have no physical significance. If the states of motion of the observer and the light source are equivalent, l0 is given, such that U can be calculated via the triangular relations illustrated in [1,2],Figure 1.
In the present work, the time of an event is measured using the following method. Both the observer and a clock are placed at the origin. When the light signal representing the occurrence of an event reaches the observer, the light arrival time will correspond with the time indicated by the clock. The advantage of the correspondence is that it is always related to the position of the observer who employs the clock. As seen in Figure 1, spatial point O3 can be defined based on the position of the light source when emitting light at 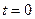 , and spatial point O2 can be defined based on the position of the observer when receiving light at
, and spatial point O2 can be defined based on the position of the observer when receiving light at 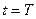 . However, the means of defining spatial point O1 at which the observer is located when the light source emits light at
. However, the means of defining spatial point O1 at which the observer is located when the light source emits light at 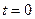 is not obvious. To solve this problem, the concepts of absolute rest (i.e.,
is not obvious. To solve this problem, the concepts of absolute rest (i.e., 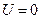 ) and absolute motion (i.e.,
) and absolute motion (i.e., 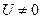 ) are introduced. We respectively substitute the single moving observer at H0 and H with two observers H1 and H2 at rest at spatial points O1 and O2, respectively, while light source A is at rest at spatial point O3. Each of the observers and the light source employ calibrated standard clocks, and A emits a light signal at
) are introduced. We respectively substitute the single moving observer at H0 and H with two observers H1 and H2 at rest at spatial points O1 and O2, respectively, while light source A is at rest at spatial point O3. Each of the observers and the light source employ calibrated standard clocks, and A emits a light signal at 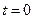 , denoted as event R0. When observer H1 receives the light signal traveling at c, the clock reading is T0, and when H2 receives it, the reading is T. As such, the distances
, denoted as event R0. When observer H1 receives the light signal traveling at c, the clock reading is T0, and when H2 receives it, the reading is T. As such, the distances 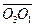 and
and 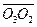 can be defined based on the respective travel times of the light signal as follows:
can be defined based on the respective travel times of the light signal as follows:
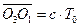 , (1)
, (1)
and
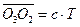 . (2)
. (2)
According to the triangular relations shown in Figure 1, the transformation of event R0 between observers H1 and H2 is given as follows.
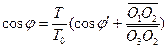 (3)
(3)
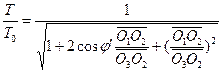 (4)
(4)
Here, 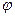 is the angle between the line O3O1 and the x axis, and
is the angle between the line O3O1 and the x axis, and 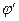 is the angle between the line O3O2 and the x axis.
is the angle between the line O3O2 and the x axis.
Returning now to the condition of a single moving observer, we assume that, in system S, both the observer H and light source A employ a calibrated standard clock. At the instant of event R, light source A is at spatial point O3, and observer H is at O1. The instant at which the light signal reaches spatial point O1 corresponds with an S clock reading of T0. When observer H receives the light signal, the reading is T, and H is at O2.
Of course, H cannot observe event R at point O1. To solve this problem, another observer H-is placed in system S at point O1 corresponding with 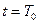 , where the position of H- is employed to define spatial point O1. Then, the transformation of event R between observers H- and H can be obtained through Equation (3) as follows.
, where the position of H- is employed to define spatial point O1. Then, the transformation of event R between observers H- and H can be obtained through Equation (3) as follows.
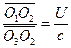 (5)
(5)
Hence, Equations (3) and (4) can be rewritten as follows.
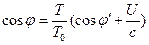 (6)
(6)
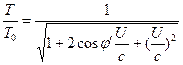 (7)
(7)
e also observe that, for 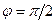 , Equations (6) and (7) simplify to the following.
, Equations (6) and (7) simplify to the following.
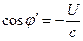 (8)
(8)
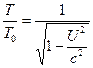 (9)
(9)
Therefore, based on the above analysis, a simple method for determining U can be obtained from Equation (6), given that 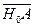 (φ) is known.
(φ) is known.
For the purpose of simplicity, a light source with an equivalent state of motion as that of the observers is chosen as the reference frame. An observer is set in the center of a straight rigid bar in uniform linear motion, and light signals from different positions on the bar arrive at the observer at different times. The observer detects bar deflection at the observer's position with a deflection angle 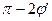 that can be obtained from Equation (8).
that can be obtained from Equation (8).
Through this method, the state of motion of a spacecraft could be determined from a closed cabin.
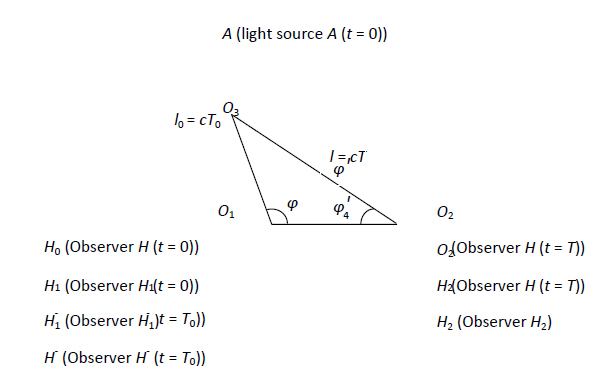
Figure 1: states of motion of the observer and the light source
The relativity of length
In the above analysis, two lengths have been introduced, i.e., 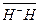 and
and 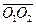 . In this case, we consider the length of a bar that is assumed to be a stationary rigid bar of length L within its coordinate system, for which L is measured with a stationary staff gauge, and where the bar axis is coincident with the x axis of a coordinate system that moves with uniform linear motion along the +x direction at an absolute velocity U. It is assumed that L is determined by the two operations defined below.
. In this case, we consider the length of a bar that is assumed to be a stationary rigid bar of length L within its coordinate system, for which L is measured with a stationary staff gauge, and where the bar axis is coincident with the x axis of a coordinate system that moves with uniform linear motion along the +x direction at an absolute velocity U. It is assumed that L is determined by the two operations defined below.
(a) The observer resides in the same moving coordinate system as does the bar and staff gauge, and L is measured by superposing the bar and staff gauge.
(b) By the aid of several clocks positioned in stationary coordinates, which move in synchronization, the observer measures the positions of the two ends of the bar in stationary coordinates at a specific moment t, and the distance between the two positions is measured with the stationary staff gauge. 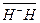 is the length calculated from operation (a), which is denoted herein as the bar length in the moving coordinate.
is the length calculated from operation (a), which is denoted herein as the bar length in the moving coordinate. 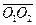 is the length calculated from operation (b), which is denoted herein as the length of a moving bar in the stationary coordinate. It is obvious that
is the length calculated from operation (b), which is denoted herein as the length of a moving bar in the stationary coordinate. It is obvious that 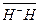 and
and 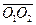 are different.
are different.
We assume that, in system S, observer H- is in the same state of motion as H. Then, as shown in Figure 1, H- is at point O1 when receiving the light signal at 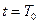 , and, simultaneously, observer H is at point O4. Therefore, t=0.04
, and, simultaneously, observer H is at point O4. Therefore, t=0.04
is the distance between H- and H at 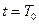 , and
, and
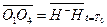 . (10)
. (10)
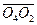 is the distance traveled by observer H in the interval from T0 to T, such that
is the distance traveled by observer H in the interval from T0 to T, such that
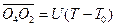 . (11)
. (11)
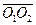 is the distance between H- at
is the distance between H- at 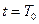 and H at
and H at 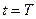 , such that
, such that
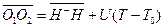 . (12)
. (12)
As such, the following expression can be deduced.
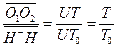 (13)
(13)
Next, we will consider the coordinate and time transformations between two moving coordinate systems, both of which move with a uniform linear velocity, which represents a new explanation of the Lorentz transformation.
Assuming that observer H (in system S), observer H' (in system S'), and light source A'' (in system S'') all employ calibrated standard clocks individually, and, at 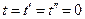 , light source A'' emits a light signal, denoted as event R''. At the instant of event R'', A'' is at point O3, and observers H and H' are coincident. When observer H receives the light signal, the reading of the S clock is T, and H is at point O1. When observer H' receives the light signal, the reading of the S' clock is T', and H' is at point O2. Then, the transformation of event R'' between observers H' and H can be calculated from Equation (3), where
, light source A'' emits a light signal, denoted as event R''. At the instant of event R'', A'' is at point O3, and observers H and H' are coincident. When observer H receives the light signal, the reading of the S clock is T, and H is at point O1. When observer H' receives the light signal, the reading of the S' clock is T', and H' is at point O2. Then, the transformation of event R'' between observers H' and H can be calculated from Equation (3), where
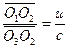 . (14)
. (14)
Here, u is the relative velocity between observers H' and H, which yields the following transformations.
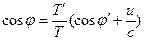 (15)
(15)
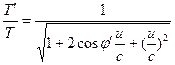 (16)
(16)
From 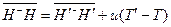 , the following relations can be derived:
, the following relations can be derived:
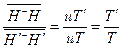 . (17)
. (17)
When 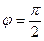 and
and 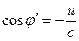 , Equation (16) simplifies to
, Equation (16) simplifies to
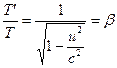 . (18)
. (18)
Therefore, the following transformation relations can be deduced:
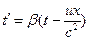 , (19)
, (19)
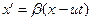 , (20)
, (20)
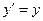 , (21)
, (21)
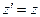 . (22)
. (22)
Moreover, when 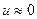 ,
,
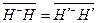 , (23)
, (23)
and
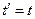 , (24)
, (24)
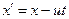 , (25)
, (25)
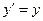 , (26)
, (26)
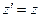 . (27)
. (27)
References
- Stephen William Hawking (Author), Mingxian Xu, Zhongchao Wu (Translator). A Brief History of Time.Changsha: Hunan Science and Technology Press, 2002
- Qingzhang Zheng, Shizhi Zheng. The theory of relativity and spacetime. Taiyuan: Shanxi Science and Technology Press, 2000

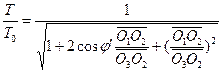 (4)
(4) 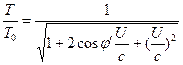 (7)
(7)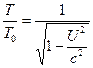 (9)
(9) 
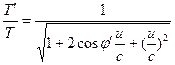 (16)
(16) 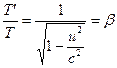 . (18)
. (18)