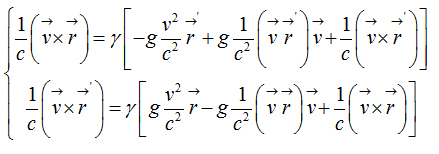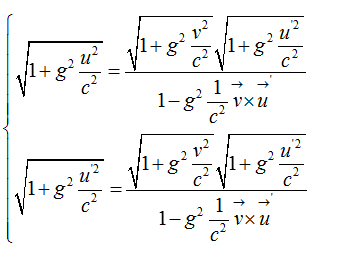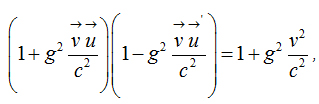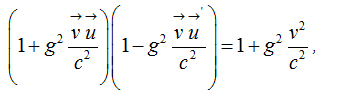Abstract
In this article, we derive new transformation equations of relativity in 3D using the following guidelines:
- We use only vector notations to obtain the new transformation equations in a general form.
- In the process of deriving new transformation equations in vector form, we also keep the term
- Newly obtained transformation equations need to satisfy the linear transformation fundamental laws.
- Addition of velocities we calculate in two different ways: by linear superposition and by differentiation, and they need to coincide each other.
If not, then we force them to match for obtaining the final relation between coefficients. After using the above mentioned general guidelines, we obtain direct and inverse transformation equations named the Armenian transformation equations, which are the replacement for the Lorentz transformation equations.
Introduction to the Armenian transformation equations in 3D
The Lorentz transformation equations, as we know them, in two dimensional time-space (t,x) or in four-dimensional time-space (t,r), when the inertial systems move at a constant relative velocity v along one of the chosen axis, are linear orthogonal transformations. In these cases Lorentz transformations are a group and satisfy the fundamental linear transformation rules: L(v)L(u')= L(u). Where the resultant transformation is a Lorentz transformation as well with the 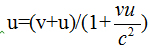
In general, when the relative resultant velocity velocity of the inertial systems S and S have an arbitrary direction, then the Lorentz transformation is not a group and are therefore less discussed as a case. Only a few brave authors mention and discuss this general case (axes of the inertial systems they take parallel to each other as usual). The main linear transformation law fails for the general Lorentz transformation. Since, however, a resultant transformation must be a Lorentz transformation as well, physicist need therefore to add an extra artificial transformation called the Thomas precession, to compensate for the error. This is the Achilles heel in the Lorentz transformation equations in 3D and more precisely in all special and general theory of relativity. Therefore it is an imperative, that the Lorentz transformation equations be replaced by new ones, which must be consistent with linear transformation fundamental laws and have a common sense in respect to reality. Here we shall derive these New transformation equations, using pure mathematical logic without any limitations and the following three postulates:
- All physical laws have the same mathematical(tensor) form in all inertial systems.
- There exists a boundary velocity, denoted as c, between micro and macro worlds, which is the same in all inertial systems.
- The simplest transformation equations of the moving particle between two inertial systems have only when relative velocity, measured in two inertial systems, satisfy the reciprocal relation
These first two postulates are almost the same as the Special Relativity Theory postulates, but the third postulate is quite new and necessary for receiving the simplest transformation equations without ambiguity problems in orientation of the inertial systems axes.
All authors that I know, derive the Lorentz transformation equations using two Cartesian coordinates t, x) or as a general way using four Cartesian coordinates (t, x, y, z). Nobody (that I know of) uses vector notations to derive general transformation equations for relativity. Many authors artificially construct 3D Lorentz transformation equations in vector form using one dimensional Lorentz transformation equations and therefore those generalized results cannot be correct. The laws of logic tell us, that we need to go from the general case to the special case. That’s why we derive our new transformation equations using the most general considerations and adapting vector notation. The great merit of the vectors in the theoretical and applied problems is that equations describing physical phenomena can be formulated without reference to any particular coordinate system, without worry that coordinate systems axes are parallel to each other or not. However, in actually carrying out the calculations we need to find a suitable coordinate system (our third postulate) where equations can have the simplest form. Therefore to receive the correct transformation equations we need to use only vector notations and focus on it entirely. Using this new promising approach and one additional postulate we derive truly correct transformation equations in the general and simplest form.
The other question can arise - why are we calling our newly received transformation equations the Armenian Transformation Equations? The answer is very simple. This research was done for more than 40 years in Armenia by an Armenian and the manuscripts were written in Armenian. This research is purely from the mind of an Armenian and from the Holy land of Armenia, therefore we can rightfully call these newly derived transformation equations the Armenian Transformation Equations and the theory the Armenian Theory of Relativity or ATR.
Summary of the Armenian transformation equations In 3D
Direct and Inverse Armenian transformation equations
Direct transformations 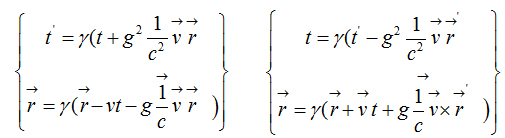 Inverse transformations
Inverse transformations
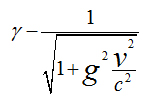
Armenian gamma function
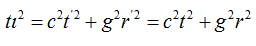
Invariant Armenian interval
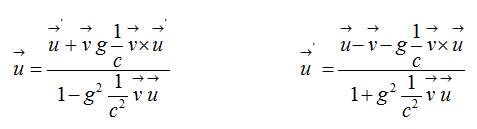
Addition and subtraction of the velocities
Addition of the velocities 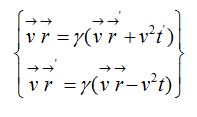 Subtraction of the velocities
Subtraction of the velocities
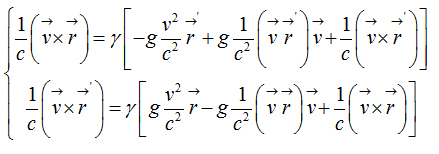
Important relations 1
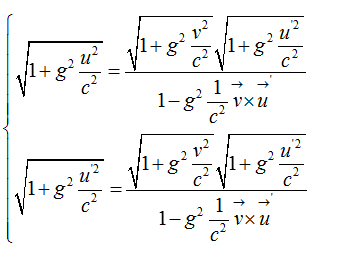
Important relations 2
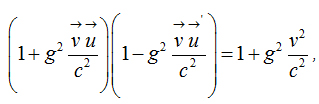
Important relations 3
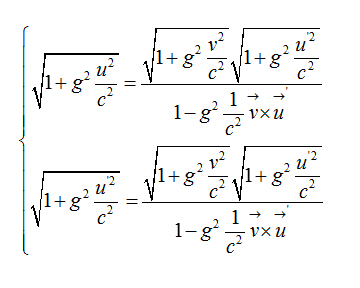
Important relation 4
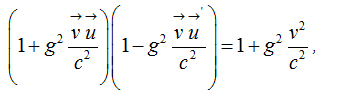
where coefficient sg is a real constant number characterizing the time-space medium.
References
- Aharoni J (1959) The Special Theory of Relativity 41-47, 53-55.
- Clyde Davenport (1991) A complex Calculus with Applications to Special Relativity.
- David Bohm (1965) The Special Theory of Relativity. 36-125.
- Lorentz HA (1923) Electromagnetic phenomena in a system moving with any velocity less than that of light, (Dover).
- Louis Brand (1955) Vector and Tensor Analysis (John Wiley & Sons, Inc., New York).
- Moller C (1972) The Theory of Relativity, Oxford University Press.
- Robertson HP (1968) Thomas W. Noonan, Relativity and Cosmology, W. B. Saunders, London.
- Resnick R, Halliday D (1992) Basic Concepts in Relativity. Macmillan Publishing Company, NY.
- Rosser WGV (1964) An Introduction to The Theory of Relativity, Butterworts, London.
- Stephenson, Kilminster (1958) Special relativity for Physicists, (London).
- Thomas LH (1927) The Kinematics of an Electron with an Axis, (Phil.Magazine and Journal of Science, London).
- Zhang ZY (1997) Special Relativity and Its Experimental Foundations, (World Scientific), pp. 22-49.

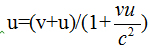
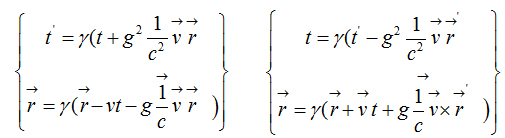 Inverse transformations
Inverse transformations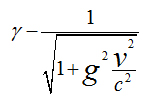
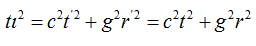
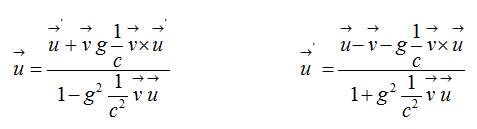
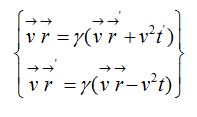 Subtraction of the velocities
Subtraction of the velocities