Take a look at the Recent articles

Abstract

Neurodegenerative diseases and traumatic brain injury, whose hallmark features are the presence of focal axonal swellings (FAS), are leading causes of cognitive dysfunction. By leveraging biophysical observations of FAS statistics, we develop a theoretical model of functional neural network activity driven by adaptive changes from plasticity. Based upon the FORCE model of Sussillo and Abbott [1], our innovations highlight the role of plasticity in overcoming injuries and degeneration of neurons in a network architecture. We provide a quantitative measure, on a network level, of cognitive deficits arising from injury. We demonstrate that plasticity is capable of overcoming mild injuries while failing to compensate for more severe injuries. Such injuries are characterized by their underlying effect on spike trains propagating through the neurons in a network architecture. Specifically, spike trains can be filtered in firing rate, or blocked under more severe FAS. The level of injury dictates the FORCE model’s ability to produce a desired output functionality (and associated behavior) and allows for quantitative metrics for accessing cognitive and behavioral deficits. Thus a direct link between FAS in neural networks and compromised functional response can be established. The theoretical framework developed is a promising computational framework for providing a deeper understanding of the cognitive deficits arising in, for instance, Alzheimer’s, Parkinson’s, Multiple-Sclerosis, and TBI.

Introduction

Neural plasticity plays a fundamental role in learning, memory and other executive functions. Although aging correlates with a natural decline in such cognitive abilities [1], notable deficits are usually associated with degenerative diseases or traumatic brain injuries (TBI). At present, limitations in biophysical measurements and neural recordings make it extremely difficult to extract the underlying mechanisms responsible for dysfunctions in neural networks, especially when circuits display intrinsically complex behavior and functional activity. Typically, the output patterns of such networks are associated with stimulus-induced behavior, thus suggesting that the neuronal networks are critical in data acquisition, processing and decision-making. In this manuscript, we build upon a recent model of neural plasticity and learning by Sussillo and Abbott [2] that captures key aspects of adaptive functional circuits in the brain. Specifically, we combine state-of-the-art biophysical observations about the role of focal axonal swellings in neurodegenerative diseases [3-5] and traumatic brain injury (TBI) [6,7] with their known impact on spike train encoding [8-10]. In doing so, we can quantity the cognitive deficits and compromised functional activity of the brain and the impact on its associated control (behavioral) protocols. Such a data-driven computational study is a first step to understanding on a network level the deleterious impact, in a quantifiable manner, of neurodegeneration and TBI.

A recent mathematical model of neuronal networks with feedback and control pioneered by Sussillo and Abbott [1], known as the FORCE model, has shown that even chaotic networks can be trained to produce a variety of output patterns, suggesting that synaptic plasticity may be more powerful than generally appreciated. The FORCE model thus provides a quantitative framework for understanding neural plasticity, allowing for robust encoding of given stereotyped input stimulus to prescribed output neural activity. Importantly, the FORCE model suggests an underlying biological mechanism by which collections of neurons can organize their behavior into target functions in order to enact sophisticated control protocols associated with behavior and/or functional activity. In living organisms, these target functions encode important biological functions such as motor actions [11] or sensory information [12,13]. In fact, simpler organisms like the nematode  exhibit complex motor behaviors by combining a small number of body-shape modes [11], thus suggesting how target functions can be used for simple tasks like locomotion. In this study, we simulate networks with these key properties but in the presence of injurious effects arising from FAS that are believed to occur in many neural pathologies and TBI. Specifically, we combine biologically derived FAS statistics with their impact on spike train encoding [8-10] in order to characterize damaged neuronal networks. We also develop new metrics to track anomalies in the collective neural activity and failures in their overall ability to learn and reproduce target output functions.

More broadly, this study addresses the critically important effects of cognitive and behavioral deficits arising from FAS.  FAS is a hallmark feature of TBI which is annually responsible for millions of hospitalizations, with at least 1.7 million cases in the United States alone [14,15]. Reports estimate that 57 million people worldwide experienced some form of TBI [16]. It targeted around 15% of all veterans of the Iraq and Afghanistan wars, with blast injuries being the signature wound of these conflicts [15,16]. Numerous studies show that even mild concussions, if induced repeatedly, can lead to permanent brain damage; the issue is constantly debated in the sports media, but especially in football [17]. The pathophysiology of TBI is heterogeneous [18,19,16]. However, all severities of TBI trigger axonal damage widespread over a large number of neurons [20].

Injured axons are thus a diagnostic marker for cognitive and behavioral deficits [3,21], both in animals and humans [22-25]. In extreme cases, axons are sheared or disconnected, leading to cell death. But even in mild TBI, injured axons undergo changes culminating in FAS [6,7,25-28]. FAS can lead to dramatic changes in axon diameters, potentially interrupting axonal transport [29,30] and/or significantly impairing the underlying spike train propagation responsible for encoding information in neural activity [8-10,31].

Interestingly, many leading neurodegenerative diseases, which affects orders of magnitude more people than TBI, also display FAS as a hallmark feature. Indeed, modeling the effect of FAS in neuronal networks can also shine new light in neuropathologies where they are implicated, such as Alzheimer’s disease [4,5], Creutzfeldt-Jakob’s disease [32], HIV dementia [33], Multiple Sclerosis [34,35] and Parkinson’s disease [36]. For both neurodegeneration and TBI, FAS leads to compromised network functionality and control in the FORCE model. Thus, a drop in network performance can be interpreted as a proxy for cognitive or behavioral deficits, opening possibilities for novel diagnostic techniques in these deleterious and widespread diseases. Ultimately, we provide a first study linking connective plasticity and pathological developments after brain trauma or neurodegeneration.

Materials and methods

The modeling of neuronal networks is one of the most vibrant fields of computational neuroscience [37-39]. In our simulations we use the FORCE learning protocol [1]. The rationale is that before learning, both network activity and its output are chaotic. The network is then trained, i.e. synaptic weights are adjusted to match its output to a given target function.  Sussillo and Abbott [1] define the training of a neural network as a process through which parameters (typically synaptic strengths) are modified on the basis of output errors until a desired response is produced. Figure 1 illustrates the training process. After training, the network activity produces the coherent pattern periodically without requiring any additional weighting modification. Our contribution is a comprehensive study of how the effects attributed to FAS jeopardize the network functionality and training of the network. The network learning deficits have a clear biophysical interpretation, and anomalies in the injured output can be described quantitatively. Specifically, the normed distance between the target function and output of the network can be thought of as a measure for cognitive and/or behavioral deficit. Thus a trained and uninjured network would be able to match the target function whereas an injured (neurodegenerated) network would not accurately produce the desired target function. This connection will be explored further in what follows.

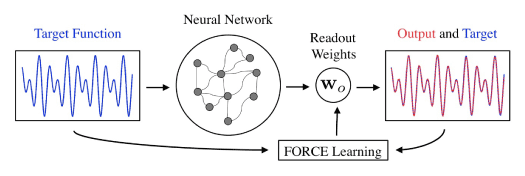
Figure 1. Schematic diagram of basic FORCE learning model [1]. An artificial neural network is given an input in the form of a target function. The network output is generated via a weighted sum of neuron firing rates. Weights assigned to each neuron are adjusted using FORCE learning to achieve an output similar to the target function. Perfect functionality is achieved if the output is identical to the target function. In contrast, cognitive deficits will occur when the output is unable to produce the expected target function.

Training networks with FORCE

Training neural networks usually consists in applying a sequence of modifications that gradually improve the output. In FORCE learning [1], errors are maintained at small levels throughout the simulation. During the training period the learning scheme, rather than working to lower error, lowers the amount of training needed at each step. By the end of the training period, output weights have converged towards a value that recreates the periodic target function without further modification. During the testing phase of the FORCE learning simulation the target function is repeated periodically without any changes to the output weights. Networks initially exhibiting chaotic dynamics have been shown to achieve faster learning agreeing with several results which have shown that neural circuits exhibit chaotic dynamics for spontaneous spiking activity [40-43]

FORCE learning has been shown to be successful in several contexts. Most notable, it allows an artificial neural network to reconstruct a periodic target function. However, networks may also be trained to reproduce a non-periodic signal for a finite time, after which the output deviates from the target function while appearing qualitatively similar [1]. Networks may also train multiple outputs simultaneously. This is shown later in our results when an network trained using the FORCE protocol is used to effectively control the bi-modal simulated motion a worm.

When introducing an injury, through the impact of FAS [8-10], to the network it is unclear how exactly injury or neurodegeneration may affect neural plasticity on a biological/chemical level. Indeed, a current lack of biophysical evidence in this area is what has led to postulated theoretical models like the FORCE learning and spike train deterioration from FAS [8-10]. As a consequence, what we propose will be built upon reasonable assumptions that are validated with experimental evidence whenever possible. Additional complications in modeling arise when considering damaged networks before and after training. Specifically, if the network is injured prior to the learning phase of the simulation then we may still expect learning to achieve the desired post-learning outcome of a network that periodically reproduces the target function without further weight modifications. However such a network may experience difficulty during the training phase and fail to reach a stable set of output weights. If injured after training but before testing the resulting output signal will show the effect injury has on a network which has already learned a signal.

Regardless of when the injury occurs, in the FORCE algorithm, errors are always kept small, even at the beginning of the training process. Thus the goal of training is not significant error reduction, but rather reducing the amount of modification needed to keep the errors small. By the end of the training period, modification is no longer needed, and the network can generate the desired output autonomously. More precisely, modifications are stronger at the beginning of the training process and tend to zero as the network is trained, i.e. it is a self-tuning system for a given target function.

Network models

Over the past few decades, computational neuroscience efforts have developed a host of models for modeling individual neurons as well as network architectures [37-39]. Here, we will consider the network temporal dynamics using a firing rate model. Specifically, the network temporal dynamics is quantified by the firing rate vector r(t) of all it’s neurons. A more concise description of the network collective behavior is achieved by a weighted sum of these firing rates labeled as the network output z(t). FORCE learning adjusts the readout weights w_o to reproduce a specific target function that has been supplied to the network (See Figure 1). A list of all the model variables can be found in Table 1. The algorithm updating the network state and output function is outlined below:

Symbol	Description
x	vector of firing rates
r = tanh(x)	rectified firing
τ	time constant
M	connectivity matrix
wo	output weights
z	network output

Table 1. List of key variables of the FORCE model architecture using a firing rate model.

i. Update Firing Rates:        x(t+△t) = (1−△t)x+Mr△t.                                                                                                     (1)

ii. Rectify Firing Rates:       r = tanh(x).                                                                                                                               (2)

iii. Calculate Output:          z = woT r                                                                                                                                 (3)

iv. Re-weight wo with FORCE.

The connectivity matrix M is sparse, with non-zero entries normally distributed and scaled. Proper scaling of parameters prevents the state vector from blowing up or vanishing. Initial readout weights w_o are random but they change at each step of the training period.

This algorithm will be used to train our network model to a variety of target functions. The connectivity matrix becomes critical in what follows as we will modify it according to various injury and/or neurodegeneration protocols. The level of modification of M determines the extent of injury to the network.

Modeling injurious effects of FAS

Focal Axonal Swellings (FAS) are ubiquitous in neurodegeneration, aging and TBI. FAS can lead to a remarkable 30-fold increase in axon diameter [29, 30]. Additionally, recent works demonstrate that critical changes in axonal morphology can impair the underlying spike train propagation responsible for encoding information in neural activity. Figure 2 schematizes how we added such pathologies to neuronal networks: a fraction of axons develop swellings (in red) of different sizes and shapes proportionally to the severity of the injury. Their collective effects to the neuronal dynamics distort the output function. To date however, no electrophysiological recordings have been taken pre and post-FAS to quantify spike train dynamics. Thus the theoretical models of Maia and Kutz [8, 9, 10] provide the first and only quantification of spike train deterioration due to FAS. Using this model, we can characterize the effect of injury on the firing rate through a response function

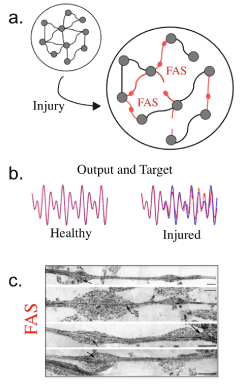
Figure 2. a. Visual comparison of healthy and injured network. Red axons that have been affected by FAS will result in decreased learning ability. b. Sample target functions and outputs taken from the same network with and without injury. Note that the uninjured network effectively reproduces the target function, while the injured network incurs noticeable errors. c. Biophysical example of axonal swellings taken from Tang-Schomer et al. [29].

ř = G(r, βj ).                                                                                                                                                                                  (4)

where ř is the firing rate after the FAS, r is the firing rate before the FAS, and β is a parameter indicating the one of three injury types applied to the network [8-10]. Specifically, axonal swellings have been shown to induce blockage (β1), reflection (β2), or filtering (β3) of neuronal spikes that comprise a spike train. The injury type is dependent upon the geometry of the swelling, with blockage being the most severe injury and filtering being the mildest effect of FAS.

From biophysical data collected on injury statistics [28], both in swelling size and frequency, we assign accordingly a certain percentage of each type of injury to the network used in simulation. For a blockage injury (β1), no signal passes the swelling so the effective firing rate of the neuron goes to zero so that ř = 0. Filtering injuries were taken to decrease the firing rate, with higher firing rates having a stronger chance of decreasing to pile-up effects in the spike train [8]. Reflection of spike trains, which only occurs for an extremely narrow range of parameter space, and thus are very rare, effectively filters the firing rate of an axon by lowering it by a factor of two so that ř = 0.5r. Note that filtering and blockage are the dominant effects and are the critical drivers in determining cognitive deficit.

Proxy for behavioral deficits

Thus far, we have mixed the notions of cognitive and behavioral deficits. Indeed, the viewpoint taken here is that impaired cognition leads to impaired behavioral performance. To demonstrate this more quantitatively, simulations were also performed using a network producing two simultaneous outputs which were used to control the motion of a two-mode (eigenworm) swimmer as studied in Refs. [11,44]. As would be expected, the motion of the two-mode crawling behavior is negatively impacted by introducing FAS into the simulated network. In this case, Table 1 is modified in order to include the two output functions and two output network weighting functions. This example directly addresses behavioral deficits as a proxy for cognitive impairment.

The network used to control the eigenworm network is more complex than the single target output system. Specifically, we have two outputs, z₁ and z₂, each modulating the activity of one of the two modes of the eigenworm. Figure 3 shows the basic configuration for consideration. The network is thus partitioned into four blocks and each is constructed to be a small world network that may be sparsely or fully connected. There are sparser connections between the four small world networks. Two of the sub-networks are labeled output networks whose firing rates provide the two outputs and two are control networks, used to aid in the learning. Each of the control networks is associated with an output network via a feedback loop. Each of the four is assigned a set of output weights and there are also feedback weights that will be used to feed the output from control (1 or 2) back into both control and output (1 or 2). The model is as follows:

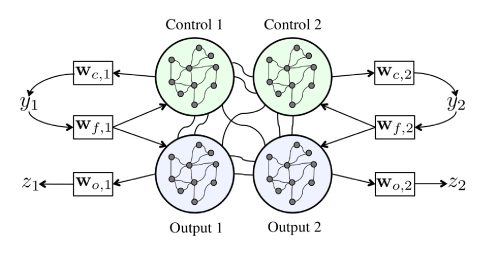
Figure 3. Eigenworm swimmer network inspired by a two-mode model for forward crawling behavior of the nematode C. elegans.

x = (1−dt)x + Mrdt + wf,1y1dt + wf,2y2dt                                                                                                                           (5a)

r = tanh(x)                                                                                                                                                                                    (5b)

z1 = wo,1Tr                                                                                                                                                                                  (5c)

z2= wo,2Tr                                                                                                                                                                                   (5d)

y1 = wc,1Tr r                                                                                                                                                                               (5e)

y2= wc,2Tr                                                                                                                                                                                   (5f)

where the following are updated with the FORCE model

wo,1, wo,2, wc,1, wc,2                                                                                                                                                                (6)

Note that each output weight vector is a column vector with as many entries as total neurons. However, only a subset of them corresponding to the indices of it’s respective network are non-zero. So w_c,2, the output weights for the second control unit, only has non-zero entries for indices corresponding to neurons in the sub-network that we are using as the second control unit. Likewise, each feedback loop from the control unit’s output back into the network only effects that control unit and the output we associate it with. Feedback from control network 1 only goes to control network 1 and output network 1 neurons, so w_f,1 only has non-zero entries for neurons in control 1 and output 1.  Note that we treat different groups of outputs differently in the learning step. Thus w_o,1 and w_c,1 are adjusted using the error from z₁ while w_o,2 and w_c,2 are adjusted using the error from z₂. Each output and each control network is given it’s own inverse correlation matrix (four in total) that is updated separately using the firing rates from it’s own neurons. The feedback loop weights and internal connectivity M were not adjusted.

Results

Metrics for cognitive deficits

Of particular interest in studying damaged network functionality was a quantitative measure of cognitive deficit. We chose to use the simplest metric possible, i.e. the summed magnitude of the difference between the target function and the simulated network output. The network output error was quantified as the summed magnitude of the error between the target function and output during the training phase of a FORCE learning scheme on an injured network. We normalized the error such that an output of zero, i.e. all neurons are blocked, resulted in an error of one. This measure of error was studied at various injury levels in order to analyze the onset of cognitive deficits due to increasing injury (neurodegeneration) levels. Figure 4 illustrates the increasing levels of injury on a network of 1000 neurons with injuries equally distributed between blocked (β1), reflected (β2), and filtered (β3) neurons. We ran the same simulation for 250 trials in order to collect a statistical sampling of the cognitive deficits. Additionally, four different injury levels where considered which resulted is notably different behavior. Data from each trial was distilled into the measure P_I(e), a probability density distribution for the error to fall within a specified range e given an injury level I. The data statistics is summarized in Table 2. An uninjured network will generally have very low error with little variance. As the injury is increased, the variance of the error increases significantly as the behavior of the network output becomes less predictable. At higher injury levels, the network tends to fail entirely, and the error once again becomes more predictable resulting in lower variance. Distributions tending towards low or high error are skewed towards the opposite levels of error.

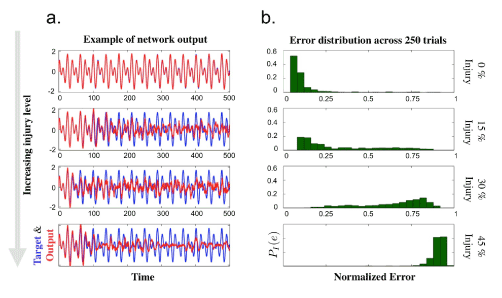
Figure 4. a. Sample outputs from networks during training phase superimposed with target function. The injury level increases from top to bottom, ranging from 0%, 15%, 30%, and 45% of neurons being affected. Injury types are evenly divided between blockage, reflection, and filtering injuries. b. Histogram of error in network output taken as summed magnitude of difference between target and output functions. The error is normalized such that an output which is uniformly zero (a completely blocked network) will have error equal to one. Data is taken from 250 trials at each injury level using 1000 neurons.

Injury Level	μ	σ2	γ1
0%	0.1183	0.0146	3.9857
15%	0.3235	0.0525	0.8402
30%	0.6511	0.0347	-0.829
45%	0.9076	0.0016	-3.6571

Table 2. Statistical properties of output error from Figure 4. Mean, variance, and skewness are given respectively for each injury level

In order to measure error in network output, a standard L¹ (or summed magnitude) measure was used. Error was taken to be the sum of absolute differences between the training function and neural output and then normalized via multiplication by a constant factor so that a neural network output of zero (a network that is completely blocked) would correspond to an error of one. There are several reasons for why this metric was chosen. First, the normalization allowed us to measure error on a scale between 0 (a perfect output) and 1 (no neural activity at all), and while higher errors were possible, they were not observed. The L¹ also has advantages of the maximum error metric because small spikes in the error would not result in a high measurement for the entire simulation. Rather, significant errors were the result of the learning failing over a longer period of time which was often observed at higher levels of injury.

Progression of FAS & injury effects

The progression of the network output error was also studied in the context of a single injury type. Simulations were run using the same network from Figure 4 with injury levels running from zero to eighty percent. The average normalized error and the standard deviations are plotted in Figure 5. For intermediate levels of injury, there is a large spread of errors present with increasing error as injury is increased. At high levels of injury the error levels off towards it’s maximum value of one. The spread of values for the error at high injury becomes very small, as expected since the network completely fails with each trial.

Of particular interest in studying the onset of network error with gradually increasing injury was the behavior observed when the three individual types of injuries were used. Blockage and reflection behaved similarly, asymptotically approaching the maximum level of error by the time injury was taken to be eighty percent. The filtering injury resulted in qualitative different behavior in the error taken at various injury levels, not reaching the limiting value of maximum error in the range of injuries studied, thus suggesting filter to be more robust in networks than blockage and reflection. This is not unexpected as blockage (or axotomy) and reflection are more severe injury types.

Synaptic re-weighting under injury

Recall that network output is generated via a weighted sum of the activity of each neuron. In the FORCE learning model these weights are adapted to produce the desired output. Using the same simulation set-up as for studying the error of the network output, we studied how the learning scheme may differ between transmitting and injured neurons. Figure 6 illustrates that depending on the type of injury there are very different results. As before, filtered neurons differ in behavior from blockage and reflection. The quantity ⟨wo(t)⟩ was taken to be the mean magnitude of output weight for the neural network at some time t during the course of the simulation. As learning proceeds, this weight is observed to increase. For a healthy network the change would be expected to level off after a certain period of time longer than the simulation used. However, when the network is injured and we observe the average magnitude of ouput weights for injured and transmitting neurons separately we see that the increase in output weights for injured neurons is different than that for healthy neurons. We also observe that the filtered neurons behave differently, exhibiting a sharp increase in ⟨wo(t)⟩. Interestingly, since there is a greater increase in the change in output weights for filtered neurons, they could potentially be more effected by a limit on plasticity, or dynamic range of neural reweighting.

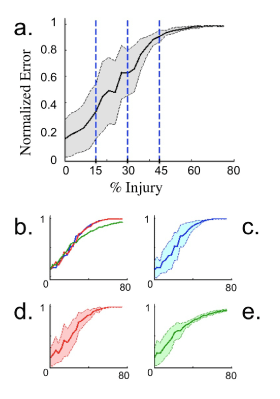
 Figure 5. Plot of normalized error averaged over 50 trials during the training phase of a network with injury using 1000 neurons. Shaded regions indicate one standard deviation above and below mean error. a. Injury type for neurons is divided evenly between blockage, reflection, and filtering. The three vertical lines along with vertical axis indicate injury levels present in Figure 4. b. Average error for specific injury types; blockage (blue), reflection (red), and filtering (green). c.-e. Individual plots for the averaged error of each specific injury type: Blockage, reflection, and filtering. The network appears more robust to filtering than blockage and reflection.

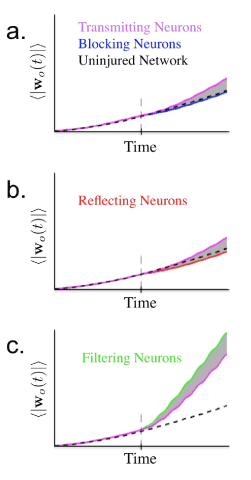Figure 6. Average magnitude of output weights (100 trials) over the course of training with injury occurring half way through simulation. Learning results in mean magnitude of output weight increasing as simulation proceeds. a. Simulation of network with 1000 neurons and 15% of neurons experiencing blockage injury. Vertical dashed line indicates time of injury. Note lesser increase of average magnitude of output weight associated with blocking neurons. b. Simulation with 15% reflecting neurons exhibiting similar behavior to blocking neurons. c. Simulation with 15% filtered neurons. Learning now results in more rapid increase in average output weights.

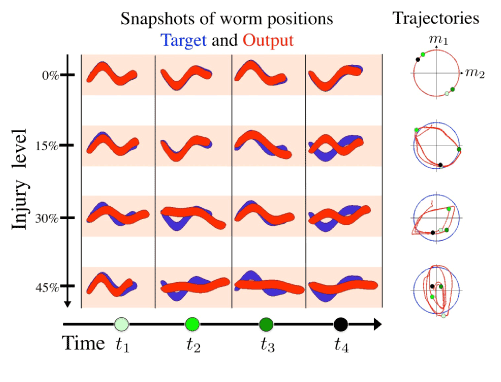
Figure 7. a. Snapshots from a simulation of a two-mode swimmer. Modes are modulated by simultaneous outputs from a network being trained using the FORCE model with varying levels of injury. Blue worms are desired output and red worms are network output. b. Trajectories of each swimmer in phase space. Blue line indicates the desired trajectory in phase space and red is trajectory of network output. Although the specific eigenmodes could be used [11], it is sufficient for demonstration purposes to use a sine and a cosine with slightly different amplitudes to construct the proof-of-concept behavioral deficit of the forward crawling motion.

Injuring a swimmer network model

To connect our model to a more concrete neural network application, we incorporate key elements of the neurosensory network of the The nematode is an important model organism due to the fact that it possesses only a small number of sensory neurons, often linked to specific stimuli [45], and its range of behavioral responses is varied yet limited, confined to swimming, crawling, turning, and performing chemotaxis, for instance. Thus it is reasonable to posit in future work a complete model of its neuronal (neurosensory integration) capabilities and evaluate the cognitive deficits that arise from FAS in such functional network.

The selection of the swimmer as a toy model to demonstrate the role of cognitive deficits and the FORCE model results from observing the behavior of a . Specifically, forward crawling is known to be dominated by a two-mode stroke motion [11], i.e., the so-called eigenworm motion. Thus the motor-neuron response to PLM stimulation produces a two-mode dominance in accordance with the eigenworm behavior given that the motor responses control muscle contraction [46]. Indeed, a constant input of sufficient strength, corresponding to a sensory stimulus, is able to drive a two-mode oscillatory behavior in the forward-motion motor neurons [44].

In Sussillo and Abbott [1], a demonstration is given of the FORCE model for a walking motion. This highlights both the learning and control aspects of the model. In such a model, 100 outputs are required to drive the walking motion. Here, we greatly simplify this by considering the forward crawling motion of c. elegans, thus we require only 2 outputs to drive the two mode forward crawl. Our objective is simply to demonstrate the compromised functional circuitry, and impaired behavior, arising form injury. Indeed, this simple example illustrates all the key features of our analysis and provides intuition about the effects of neuronal damage on a network level. Namely, it shows how damage in the FORCE model compromises both learning and control, leading to a stunted forward crawling motion as a behavioral consequence.

A simulation of the motion of a two-mode swimmer was run by constructing a network with the FORCE learning scheme which controlled each of the two modes. The model is demonstrated in Figure 3. Network outputs were each trained to be oscillatory functions modulating the superposition of two normal modes of motion for the worm. This network was injured at various levels and the motion of the worm constructed from the resulting network outputs. Snapshots of the position of the worm at various injury levels and times with the desired behavior (target function) are shown in Figure 7. These provide a clear way of observing a model of cognitive deficit due to injury. The uninjured swimmer is able to follow the pattern of motion supplied to its neural network while the injured ones have progressively more difficulty as injury level is increased. Since the swimmer is controlled by two modes, we may also use phase plane analysis to view the trajectory of these modes relative to the desired path. Plotting these phase portraits gives another picture of how the injury affects learning in the artificial neural network. Indeed, the behavioral deficit is clearly observed in a compromised crawling motion of the worm. For humans, this might correspond to other deficits in motor/executive functions due to injury.

Discussion

The modeling of neuronal networks is critical for understanding almost all cognitive and behavioral phenomenon in neuroscience [37-39]. There have been hundreds of network models proposed in the computational neuroscience literature, with varying levels of complexity, architectural configurations and capabilities. Neuronal network models are used in decision making studies, learning tasks, memory studies, control theory and most brain science modeling. The range of biophysical details may vary, with some systems being vaguely inspired from biological settings, to others that incorporate cutting edge experimental measurements. This work combines state-of-the-art neuronal network modeling with the most recent and in-depth studies of neuronal pathologies in TBI and leading neurodegenerative diseases, demonstrating the clear and ubiquitous role that focal axonal swellings play in compromised neural processing and the resulting cognitive and behavior deficits.

From a signal processing point of view, recent reviews highlight the fact that axons do more than just faithfully transmit spike train encodings from upstream to downstream neurons: they are responsible for important signal and information processing [47-50]. Thus when considered in a network architecture, it is not coincidental that FAS, axonal deformation, regional compactation, and myelin abnormalities resulting from TBI in humans [51,52], rodents [53], and swine [54], are directly related to post-traumatic cognitive, physical and psychosocial dysfunctions. In theory, the modeling is driven by the fact that geometric structure changes in the axon can drastically alter axonal functionality and spike propagation dynamics [8,9]. How such pathologies developed at a single-cell level can affect the functionality of a neural network is the focus of this work. Specifically, we introduce, for the first time to our knowledge, dynamical anomalies attributable to FAS in trainable chaotic networks [1], and compared their ability to learn and reproduce a broad range of target functions before and after injury.

Our modeling efforts are based upon firing rate models of networks of neurons [37-39] and a recent innovation of the FORCE learning protocol [1]. The FORCE model is particularly relevant as it is one of the few biophysically inspired models to address plasticity effects and network control for producing robust output patterns associated with behaviors. So although finding meaningful target functions and calibrating parameters to match specific brain circuits is an extremely challenging task, the FORCE model is one of the few to attempt to address this directly. It should be noted that other computational neuroscience models with different learning strategies or architectures might respond differently to FAS injuries. In all such models, we would expect that the integration of our FAS modeling and statistics, which is based upon state-of-the-art biophysical experiments, would also allow for a characterization of cognitive deficits in these alternative neuronal network architectures. The FORCE protocol minimizes the amount of change in connection strengths while matching the network output to a desired target function. It is unclear, however, how a fraction of nonresponsive or dysfunctional neurons would affect this plasticity strategy. Our results show that reweighting is strongly dependent on the type of axonal injury, suggesting that plasticity mechanisms after brain injury may be more sophisticated then generally appreciated, especially as filtering of firing rates can be nearly as detrimental as axotomies (blockage) in producing robust information processing.

Of particular importance in this work are the one we have introduced to evaluate cognitive deficits at a neural network level. This complements and integrates recent and ubiquitous FAS biological findings concerning FAS that rely exclusively on psychophysical of biophysical experiments. Moreover, for simpler organisms such as the nematode c. elegans, our results suggest that the network’s inability to reproduce key target functions can be directly linked to behavioral deficits. This opens up the interesting possibility of directly mapping observable declines in behavior (crawling or other executive/motor function) to injuries occurring at a cellular level in a network. We characterized the network output error statistically as a function of the injury level, estimating average error growth and variability. Indeed, a characteristic of the statistics, such as the sign of the skewness, changes as the induced injury level is increased. This statistical signature suggests a potential biophysical marker for diagnostic and pharmacological treatment protocols based upon injury level.

References

1. Sussillo D, Abbott LF (2009) Generating coherent patterns of activity from chaotic neural networks. Neuron 63: 544-557. [Crossref]
2. Burke SN, Barnes CA (2006) Neural plasticity in the ageing brain. Nat Rev Neurosci 7: 30-40. [Crossref]
3. Coleman M (2005) Axon degeneration mechanisms: commonality amid diversity. Nat Rev Neurosci 6: 889-898. [Crossref]
4. Krstic D, Knuesel I (2013) Deciphering the mechanism underlying late-onset Alzheimer disease. Nat Rev Neurol 9: 25-34. [Crossref]
5. Tsai J, Grutzendler J, Duff K, Gan WB (2004) Fibrillar amyloid deposition leads to local synaptic abnormalities and breakage of neuronal branches. Nat Neurosci 7: 1181-1183. [Crossref]
6. Hemphill MA, Dabiri BE, Gabriele S, Kerscher L, Franck C, et al. (2011) A possible role for integrin signaling in diffuse axonal injury. PLoS One 6: e22899. [Crossref]
7. Hemphill MA, Dauth S, Yu CJ, Dabiri BE, Parker KK (2015) Traumatic brain injury and the neuronal microenvironment: A potential role for neuropathological mechanotransduction. Neuron 86: 1177–1119. [Crossref]
8. Maia PD, Kutz JN (2014) Compromised axonal functionality after neurodegeneration, concussion and/or traumatic brain injury. J Comput Neurosci 27: 317-332. [Crossref]
9. Maia PD, Kutz JN (2014) Identifying critical regions for spike propagation in axon segments. J Comput Neurosci 36: 141–145.
10. Maia PD, Hemphill MA, Zehnder B, Zhang C, Parker KK, et al. (2015) Diagnostic tools for evaluating the impact of Focal Axonal Swellings arising in neurodegenerative diseases and/or traumatic brain injury. J Neurosci Methods 253: 233-243. [Crossref]
11. Stephens GJ, Johnson-Kerner B, Bialek W, Ryu WS (2008) Dimensionality and dynamics in the behavior of C. elegans. PLoS Comput Biol 4: e1000028. [Crossref]
12. Riffell JA, Shlizerman E, Sanders E, Abrell L, Medina B, et al. (2014) Hinterwirth, and J. Nathan Kutz. Flower discrimination by pollinators in a dynamic chemical environment. Science 344: 1515– 1518.
13. Shlizerman E, Riffell JA, Kutz JN (2014) Data-driven inference of network connectivity for modeling the dynamics of neural codes in the insect antennal lobe. Front Comput Neurosci 8: 70. [Crossref]
14. Faul M, Xu L, Wald MM, Coronado VG (2010) Traumatic brain injury in the united states: emergency department visits, hospitalizations, and deaths. Atlanta (GA): Centers for Disease Control and Prevention, National Center for Injury Prevention and Control.
15. Jorge RE, Acion L, White T, Tordesillas-Gutierrez D, Pierson R, et al. (2012) White matter abnormalities in veterans with mild traumatic brain injury. Am J Psychiatry 169: 1284–1291. [Crossref]
16. Xiong Y, Mahmood A, Chopp M (2013) Animal models of traumatic brain injury. Nat Rev Neurosci 14: 128-142. [Crossref]
17. Stieg PE (2014) Truth, Justice, and the NFL Way: Review: League of Denial: The NFL, Concussions, and the Battle for Truth. Cerebrum: 12. [Crossref]
18. Morrison B 3rd, Elkin BS, Dollé JP, Yarmush ML (2011) In vitro models of traumatic brain injury. Annu Rev Biomed Eng 13: 91–126. [Crossref]
19. Sharp DJ, Scott G, Leech R (2014) Network dysfunction after traumatic brain injury. Nature Reviews Neurology 10: 156–166.
20. Johnson VE, Stewart W, Smith DH (2013) Axonal pathology in traumatic brain injury. Exp Neurol 246: 35-43. [Crossref]
21. Millecamps S, Julien JP (2013) Axonal transport deficits and neurodegenerative diseases. Nat Rev Neurosci 14: 161-176. [Crossref]
22. Blumbergs PC, Scott G, Manavis J, Wainwright H, Simpson DA, et al. (1995) Topography of axonal injury as defined by amyloid precursor protein and the sector scoring method in mild and severe closed head injury. J Neurotrauma 12: 565–572. [Crossref]
23. Christman CW, Grady MS, Walker SA, Holloway KL, Povlishock JT (1994) Ultrastructural studies of diffuse axonal injury in humans. J Neurotrauma 11: 173-186. [Crossref]
24. Grady MS, McLaughlin MR, Christman CW, Valadka AB, Fligner CL, et al. (1993) The use of antibodies against neurofilament subunits for the detection of diffuse axonal injury in humans. J Neuropathol Exp Neurol 52: 143–152. [Crossref]
25. Maxwell WL, Povlishock JT, Graham DL (1997) A mechanistic analysis of nondisruptive axonal injury: a review. J Neurotrauma 14: 419-440. [Crossref]
26. Magdesian MH, Sanchez FS, Lopez M, Thostrup P, Durisic N, et al. (2012) Colman. Atomic force microscopy reveals important differences in axonal resistance to injury. Biophys J 103: 405–414. [Crossref]
27. Smith DH, Wolf JA, Lusardi TA, Lee VM, Meaney DF (1999) High tolerance and delayed elastic response of cultured axons to dynamic stretch injury. J Neurosci 19: 4263-4269. [Crossref]
28. Wang J, Hamm RJ, Povlishock JT (2011) Povlishock. Traumatic axonal injury in the optic nerve: evidence for axonal swelling, disconnection, dieback and reorganization. J Neurotrauma 28: 1185–1198. [Crossref]
29. Tang-Schomer MD, Johnson VE, Baas PW, Stewart W, Smith DH (2012) Partial interruption of axonal transport due to microtubule breakage accounts for the formation of periodic varicosities after traumatic axonal injury. Exp Neurol 233: 364–372. [Crossref]
30. Tang-Schomer MD, Patel AR, Baas PW, Smith DH (2010) Mechanical breaking of microtubules in axons during dynamic stretch injury underlies delayed elasticity, microtubule disassembly, and axon degeneration. FASEB J 24: 1401–1410. [Crossref]
31. Katarina V. Kolaric, Gemma Thomson, Julia M. Edgar, and Angus M Brown (2013) Focal axonal swellings and associated ultrastructural changes attenuate conduction velocity in central nervous system axons: a computer modeling study. Physiol Rep 1: e00059. [Crossref]
32. Liberski PP, Budka H (1999) Neuroaxonal pathology in Creutzfeldt-Jakob disease. Acta Neuropathol 97: 329-334. [Crossref]
33. Adle-Biassette H, Chrétien F, Wingertsmann L, Héry C, Ereau T, et al. (1999) Neuronal apoptosis does not correlate with dementia in HIV infection but is related to microglial activation and axonal damage. Neuropathol Appl Neurobiol 25: 123-133. [Crossref]
34. Ferguson B, Matyszak MK, Esiri MM, Perry VH (1997) Axonal damage in acute multiple sclerosis lesions. Brain 120: 393-399. [Crossref]
35. Trapp BD, Peterson J, Ransohoff RM, Rudick R, Mörk S, et al. (1998) Axonal transection in the lesions of multiple sclerosis. N Engl J Med 338: 278-285. [Crossref]
36. Galvin JE, Uryu K, Lee VM, Trojanowski JQ (1999) Axon pathology in Parkinson's disease and Lewy body dementia hippocampus contains alpha-, beta-, and gamma-synuclein. Proc Natl Acad Sci U S A 96: 13450-13455. [Crossref]
37. Dayan P, Abbot LF (2001) Theoretical neuroscience. MIT Press, USA.
38. Ermentrout GB, Terman DH (2010) Mathematical Foundations of Neuroscience. Springer.
39. Richard Naud Wulfram Gerstner, Kistler WM, Paninski L (2014) Neuronal Dynamics. Cambridge University Press.
40. Amit DJ, Brunel N (1997) Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex 7: 237–252. [Crossref]
41. Brunel N (2000) Dynamics of networks of randomly connected excitatory and inhibitory spiking neurons. J Physiol Paris 94: 445-463. [Crossref]
42. Sompolinsky H, Crisanti A, Sommers HJ (1988) Chaos in Random Neural Networks. Phys Rev Lett 61: 259-262. [Crossref]
43. van Vreeswijk C, Sompolinsky H (1996) Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274: 1724-1726. [Crossref]
44. Kunert J, Schlizerman E, Kutz JN (2014) Low-dimensional functionality of complex network dynamics: Neuro-sensory integration in the caenorhabditis elegans connectome. Phys Rev E 89: 05280.
45. Z. Altun, L. Herndon, C. Crocker, D. H. Hall. The worm atlaa, NY, USA.
46. Sengupta P, Samuel AD (2009) Caenorhabditis elegans: a model system for systems neuroscience. Curr Opin Neurobiol 19: 637-643. [Crossref]
47. akkum DJ, Frey U, Radivojevic M, Russel TL, Muller J, et al. (2013) Tracking axonal action potential propagation on a high density micro electrode array across hundreds of sites. Nat Comm 4: 2181.
48. Bucher D, Goaillard JM (2011) Beyond faithful conduction: short-term dynamics, neuromodulation, and long-term regulation of spike propagation in the axon. Prog Neurobiol 94: 307-346.[Crossref]
49. Debanne D (2004) Information processing in the axon. Nat Rev Neurosci 5: 304-316. [Crossref]
50. Debanne D, Campanac E, Bialowas A, Carlier E, Alcaraz G (2011) Axon physiology. Physiol Rev 91: 555-602. [Crossref]
51. Liberski PP, Budka H (1999) Neuroaxonal pathology in Creutzfeldt-Jakob disease. Acta Neuropathol 97: 329-334. [Crossref]
52. Niogi SN, Mukherjee P, Ghajar J, Johnson C, Kolster RA, et al. (2008) Extent of microstructural white matter injury in postconcussive syndrome correlates with impaired cognitive reaction time: A 3t diffusion tensor imaging study of mild traumatic brain injury. AJNR Am J Neuroradiol 29: 967–973. [Crossref]
53. Rubovitch V, Ten-Bosch M, Zohar O, Harrison CR, Tempel-Brami C, et al. (2011) A mouse model of blast-induced mild traumatic brain injury. Exp Neurol 232: 280–289. [Crossref]
54. Browne KD, Chen XH, Meaney DF, Smith DH (2011) Mild traumatic brain injury and diffuse axonal injury in swine. J Neurotrauma 28: 1747-1755. [Crossref]