Purpose: Automated image analysis tools have the potential to improve the objectivity of the diagnostic process. The study and improvement of the numerical methodologies behind these tools is, therefore, crucial. Volumetric, densitometric, and fractal analysis concepts were, thus, explored in the setting of computed tomography (CT) imaging of different lung morphologies.
Material and methods: Thoracic CT scans were acquired for five sheep prior to and after smoke inhalation injury. Software was developed to segment the lungs from the digital image data and to estimate the morphometric parameters “volume”, “Hounsfield unit-density” (HU), and “fractal dimension”. These parameters were estimated for each scan, once from the complete dataset, covering the entire a range of -1000 to 399 HU, and once for 28 consecutive data subsets, with a width of 50 HU each. T-test statistics were used to investigate group differences “before” and “after” smoke inhalation, based on a 0.05 significance level.
Results: For the complete data set, group differentiation into “before” and “after” smoke in-halation was feasible only with volumetric analysis. Analysis of 28 smaller HU subsets, on the other hand, allowed group differentiation with all three morphometric parameters.
Conclusions: The analysis of small HU subsets can be helpful in differentiating groups and may be a useful approach for many image analysis projects.
Key points:
- Different lung morphologies in a smoke inhalation model could be differentiated by automated image analysis software.
- Volumetric analysis can be superior to densitometry or fractal dimension characterizations for complete lung data sets.
- Volumetric or fractal image analysis may be superior to densitometric evaluations when smaller HU-ranges are used and the significance limit is raised to 0.001.
- Fractal dimension characterizations can be as useful as volumetric descriptions.
volumetric analysis, densitometry, fractal geometry, lung morphology, smoke inhalation model, computer aided diagnoses
Computer-aided analysis of digital image data promises to become an important diagnostic tool in in radiological pulmonology. The numerical tools used for such purposes have the advantage of being reproducible, objective, and reliable, since they rely on a constantly per-forming mathematical algorithm, and are, therefore, not affected by inter- or intra-observer variability. Dinkel et al., for example, showed that computer-assisted size assessment of primary lung tumors could reduce inter-observer variability by about one-half to one-third compared to standard manual measurements [1]. Further, Wulff et al. showed that the precision and inter-rater variability of computer-assisted volumetric measurement was superior to manual estimates when the “change over time” of lesions was investigated in lung, liver, and lymph node metastases [2].
Volumetric analysis and Hounsfield unit (HU)-based densitometry are the numerical methods most often used as image analysis tools in radiological pulmonology [3]. Although the concept of fractal geometry is only rarely applied, it is perfectly suited to characterize irregular geometrical shapes in terms of the fractal dimension D. Three PubMed searches, performed in October 2016, were carried out to find out how frequently these methods were applied to lung investigations performed on (CT) image data. Each search query contained the terms “lung” and “CT”. Searches with the additional term “volumetry” or “volume analysis” yielded 1574 search results, searches with the additional term “densitometry” or “histogram analysis” yielded 293 results, and searches with the additional term “fractal” yielded only 39 results. Thus, while researchers appear to be generally aware of volume analysis and densitometry as methods, this does not seem to be the case for applications of fractal geometry. This study, therefore, placed particular focus on this concept.
The image analysis tools that were investigated in this study were applied to CT datasets of sheep lungs that were acquired “before” and “after” a smoke inhalation procedure. The data were acquired in the setting of a respiratory distress syndrome (ARDS) research project. Respiratory distress syndrome is a life-threatening illness that consists of acute hypoxemic respiratory failure with bilateral non-cardiogenic pulmonary infiltrates. Approximately 200,000 patients suffer from ARDS in the United States, each year [4]. ARDS is associated with high mortality and about one-third of patients die. In addition, in the United States, 1.25 million burn injuries occur every year and 5 to 35% suffer from concomitant smoke inhalation injuries [5,6]. Smoke inhalation frequently causes severe ARDS and significantly increases the mortality of burn victims. The pathophysiology of ARDS and its progression are not completely understood. The aim of the broader study was to characterize the morphology of ARDS following smoke inhalation injury by means of computed tomography imaging. Be-cause high quality interpretation of data is without question as important for research as it is in daily clinical diagnostics, three questions were in the foreground of this methodological investigation: One, can different lung morphologies, caused by the injury, be characterized by image analysis software that evaluates the parameters “volume,” a HU-based radiological density that will for reasons of simplicity henceforth be called “density,” and the fractal dimension, D. Two, based on the assumption that these morphometric parameters can successfully distinguish lung phenotypes, is there an optimal parameter, “volumetric analysis,” “density,” or “D,” that can distinguish between the lung morphologies “before” and “after” injuiry more significantly or more reliably than the others. As it is an established practice for radiologists to choose specific “window width” and “window level” settings when they diagnose CT images, this approach was also applied in this investigation and adapted in the sense that the sheep lungs were not only segmented in a wide HU-range from -1000 to 399 HU, but also in many subsets, where each of the subsets covered only a small HU-range. Hence, the third question is are there differences in the results for the parameters “volume,” “density,” or “D” that depend on a specified HU-range of a set. Or, simply put, is it helpful to analyze small HU-ranges.
The principal aim of this interdisciplinary study was to improve image analysis methods that can then be used to simplify the diagnostic work of radiologists.
Sheep experiment
This study was approved by the Animal Care and Use Committee of the University of Texas Medical Branch and conducted in compliance with the guidelines of the National Institutes of Health and the American Physiological Society for care and use of laboratory animals.
Five healthy adult female sheep weighing 30-45 kg were included in this study. Food was taken away 24 hours prior to the inhalation injury, but all animals had free access to water. Following induction of anesthesia with ketamine (500 mg intramuscular, 300 mg intravenously), endotracheal intubation was performed. Anesthesia was maintained using an isoflurane (1.4 – 1.8 vol%) – oxygen mixture. The right femoral artery was cannulated with a polyvinylchloride catheter (Intracath, 16-G, 24 inches, Becton Dickinson Vascular Access, Sandy, UT) for continuous measurement of systemic arterial pressure and intermittent sampling of arterial blood. A thermodilution catheter (model 93A-131-7F, Edwards Critical Care Devision, Irvine, CA) was inserted into the right external jugular vein through an introducer sheath (Edwards Lifescience, Irvine, CA) and advanced into the common pulmonary artery. A Foley urinary retention catheter was inserted.
The animals were then transferred into the Computer Tomographic unit of the Department of Radiology and received high resolution CT-scans as well as scans of the lung (as described below).
After the imaging procedure, the animals were transferred back to the Animal Critical Care Unit and received smoke inhalation injury according to an established protocol, previously described in detail [7]. In brief, the sheep, still in deep anesthesia, were insufflated with a total of 48 breaths (four sets of 12 breaths each) of cotton smoke. The smoke was applied using a modified bee smoker filled with 40 g of burning cotton toweling and connected to the tracheostomy tube via a modified endotracheal tube containing an indwelling thermistor from a pulmonary artery catheter. During the insufflation procedure, the temperature of the smoke was monitored carefully and not allowed to exceed 40°C. Arterial carboxyhemoglobin concentrations were determined immediately after each set of smoke inhalation.
After the smoke inhalation injury, the animals were mechanically ventilated and maintained under deep anesthesia using the isoflurane-oxygen mixture as described above. The sheep were resuscitated with lactated Ringer´s solution and allowed to recover for 24 hours and then received another set of CT exams (as described below).
After the imaging, the animals were transferred to the Animal Critical Care Unit and euthanized using an intravenous injection of 60 ml saturated potassium chloride. The lungs were then harvested and prepared for pathological and histological evaluations.
Computed tomography imaging
The imaging studies were performed on a second-generation DSCT system (Somatom Definition FLASH, Siemens Healthcare, Forchheim, Germany). The animals were positioned on the CT table in a prone position to simulate a physiological scanning situation for the animals.
To analyze the anatomical structures of the lung, high resolution CT scans in in- and expiration were performed, with and without contrast agent. Eighty ml of contrast medium (Isovue 370, Bracco Diagnostics Inc., Princeton, NJ) at a flow rate of 4 ml/s, followed by 40 ml of saline injected at the same flow rate, were administered. The scan parameters were as follows: attenuation-based tube current modulation; rotation time, 0.5 second; collimation, 14 x 1.2 mm; pitch, 0.7. The CT images were reconstructed in the axial, sagittal, and coronal orientation using a medium soft convolution kernel optimized for high resolution images at a 1.5 mm slice thickness with 1 mm increment.
Numerical lung analysis: Lung segmentation; volumetric analysis; densitometry; fractal dimension estimation
Lung segmentation: Methods of lung segmentation are well established [8-10]. The lung segmentation approach used in this study is described in detail in ref. [11]. An adapted threshold segmentation, guided by the low radiation attenuation of ventilated lung tissue, was applied. This approach segments those parts of the respiratory system, including the trachea and lung tissue, that correspond to the anatomical definition of a healthy lung, in which the complete lower respiratory system is partitioned. In contrast, in the case of a lung heavily affected by smoke, the segmentation approach excludes radiologically denser lung tissue. See the segmentation examples in Figure 1.
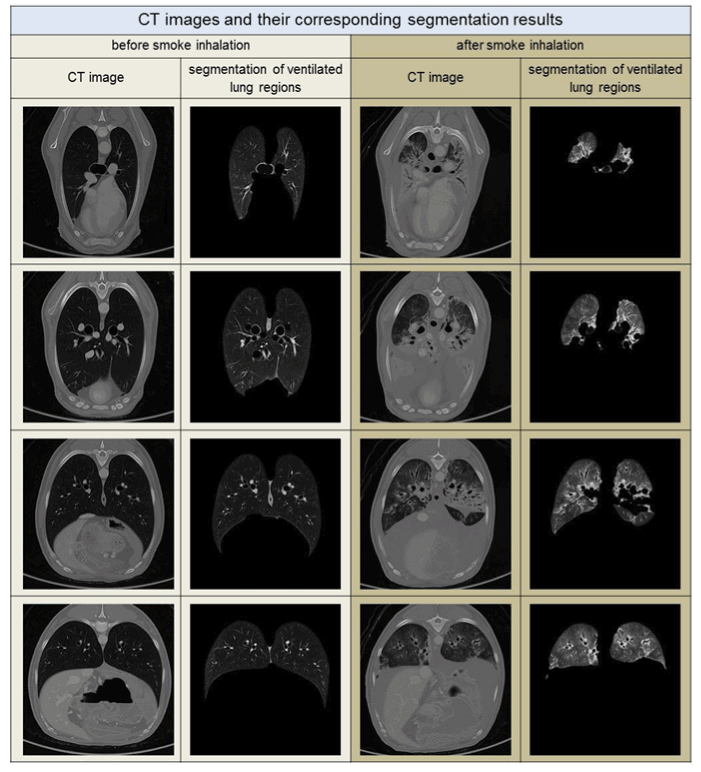
Figure 1. CT images with the corresponding segmentation results for air-filled lung regions sup-porting gas-exchange. Each column shows sectional images before and after smoke inhala-tion for similar thoracal positions. The position of the thorax changes in each row from proxi-mal to distal, top to bottom
Definition of lung subsets, volume and density analysis: The segmented data set of a sheep’s lung consists of voxels that are defined by their spatial x-, y-, and z- coordinates, and by their radiological density value, which is the HU. The complete set of a segmented lung is called L. L essentially consists of voxels with HU values in a range of -1000 to 399. This is written as L[-1000,399], where the figures in the square brackets indicate the specified HU-range of the voxels that belong to the set. Here, 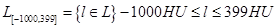 . Rarely occurring voxels, with HU values larger than 399, were ignored. The fraction of these voxels was below 0.3% and corresponded to calcified blood vessels. Since L[-1000,399] is basically identical to L, L[-1000,399] is also called the “complete set” later in the text.
. Rarely occurring voxels, with HU values larger than 399, were ignored. The fraction of these voxels was below 0.3% and corresponded to calcified blood vessels. Since L[-1000,399] is basically identical to L, L[-1000,399] is also called the “complete set” later in the text.
Next, the set L[-1000,399] was divided into 28 sets of equal width of 50 HU. These subsets began at -1000 HU and ended at 399 HU. The first subset of L[-1000,399], therefore, contained only voxels with HU values from -1000 to -951 HU, and was written, in the HU-range notation introduced above, as L[-1000,-951], where 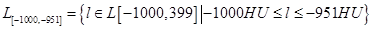 ; the second subset was, then, L[-950,-901], and so on, up to the last subset, L[350,399]. Figure 2 illustrates four different sets: The top row shows images that belong to the complete HU-range from -1000 to 399; the three bottom rows visualize images of smaller HU-range subsets L[-600,-551], L[-600,-551], and L[-600,-551].
; the second subset was, then, L[-950,-901], and so on, up to the last subset, L[350,399]. Figure 2 illustrates four different sets: The top row shows images that belong to the complete HU-range from -1000 to 399; the three bottom rows visualize images of smaller HU-range subsets L[-600,-551], L[-600,-551], and L[-600,-551].
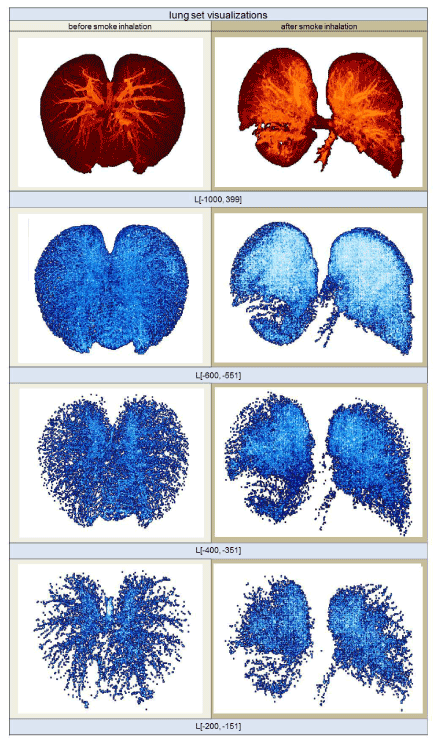
Figure 2. Volume rendering images of different HU segmentation ranges taken from the same sheep. The images on the left show the lung structures prior to smoke inhalation; the images on the right show the highly fissured lung subsets after smoke inhalation. The HU-range of the visualized subsets is given below each row.
The definitions of the parameters “volume,” “density,” and “fractal dimension” are given be-low. The parameters were applied and estimated in the same way for each segmented lung of the five different sheep, “before” and “after” the smoke inhalation experiment, within each of the HU-ranges defined above, both for the wide HU set range [-1000, 399] and for the 28 small 50 HU-wide HU-ranges.
The lung volume of a scanned sheep, v(i; L[HU-range]), was defined as the number of all voxels, p, of a set L[HU-range] multiplied by a volumetric scale factor, s, related to the voxel size:
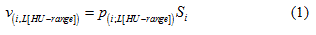
Here, “i” is the sheep number, from 1 to 5, for the group of n = 5 sheep. The “HU-range” refers to the specified lower and upper limit of the chosen HU-range of a set, L[min HU, max HU].
Next, the average volume of all n sheep at their different HU-range set specifications, volume(L[HU − range]), was of interest:
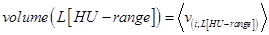 , where 〈 . 〉 denotes the average volume of the 5 sheep, each estimated for their specified HU-range.
, where 〈 . 〉 denotes the average volume of the 5 sheep, each estimated for their specified HU-range.
The “density” or mass of a scanned sheep, d(i; L[HU-range]), is defined as the sum of all HU of all voxels, q, of a set L[HU-range]:
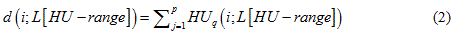
Here, “i” is again the sheep number, “HU-range” refers to the specified HU-range of a set, and “p” is the total number of voxels in a set, L[HU − range].
Next, the average “density” of all n sheep at their different HU-range set specifications, density(L[HU − range]), was of interest, which was defined as follows:
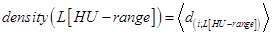 , where 〈 . 〉 denotes the average density of the 5 sheep, each at their specified HU-range.
, where 〈 . 〉 denotes the average density of the 5 sheep, each at their specified HU-range.
Measurement of the fractal dimension: The method that was used to numerically estimate the fractal dimension D was the classical “mass-radius relation”, which was applied in this study precisely as described in ref. [12]. An arbitrary voxel of the set under investigation is chosen as a center position, c. After that, the number, M, of voxels are counted within spheres of radius, r. M can, thus, also be denoted as M(r;c). If the studied structure is a fractal, M(r;c) grows as 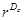 :
:
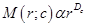 (3)
(3)
Figure 3 illustrates an example of a double logarithmic plot used to evaluate D according to the power law (3). In the graph, 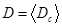 , where 〈 . 〉 denotes the average of 100 counting results for different center positions, c. The regression ranges, within which the linear regression is calculated to obtain D in such plots, were always chosen to be the same to allow a comparison of D-values from different animals and experimental groups.
, where 〈 . 〉 denotes the average of 100 counting results for different center positions, c. The regression ranges, within which the linear regression is calculated to obtain D in such plots, were always chosen to be the same to allow a comparison of D-values from different animals and experimental groups.
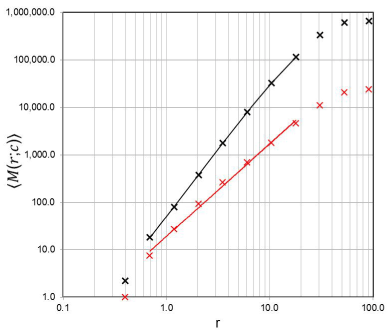
Figure 3. Example of a plot showing the counting results for the estimation of D of a lung subset in the mass-radius analysis. The x-axis shows the radius, r, in units of mm. The y-axis con-tains the averaged “mass” (i.e. the number of voxels in a binary image) within an increasing sphere set of radius, r, evaluated for 100 different, non-repeating center positions, c, of the sphere sets. The black marks and corresponding black regression line, which indicates the scaling range within which D is estimated by linear regression, correspond to the data set “before” smoke inhalation (D = 2.628 ± 0.069; correlation coefficient = 0.999; total voxel num-ber of the subset = 656023); the red marks and regression line belong to the data set “after” smoke inhalation (D = 1.956±0.106; correlation coefficient = 0.998; total voxel number of the subset = 23965).
In general, the fractal geometry concept enables the description of irregular geometrical shapes with non-integral D. The concept was introduced by B. Mandelbrot and is well de-scribed in ref. [13]. Figure 4 shows examples of such fractals. A description of this well-documented concept is not the scope of this article and can be found in refs. [14-16].
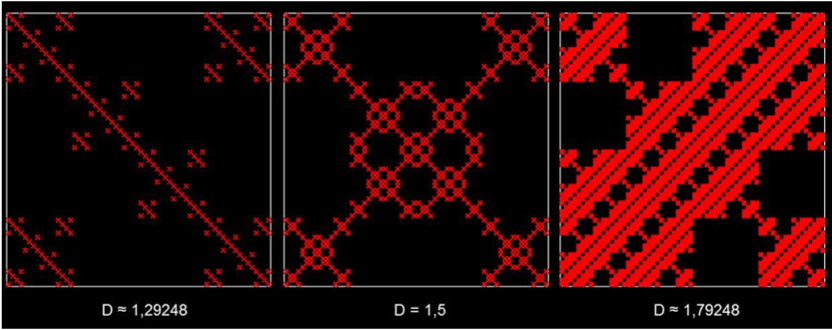
Figure 4. Examples of three numerically-constructed fractal curves. The fractal dimension val-ues are given below each image. Note that the higher the value of D is, the more “space-filling” the structure is. All of the structures possess an important property of fractals: self-similarity. This means small detail of the image will be indistinguishable from the original im-age when it is magnified to the size of the original image. This is similar to the morphological structure of the lung, in which larger airways keep bifurcating into smaller ones.
The Shapiro-Wilk test was used to test normal distribution. The f-test was used to investigate the homogeneity of variances, and paired t-tests were used to estimate the significance of differences of mean values of compared groups “before” and “after” smoke inhalation. Last, the effect strength, r, was calculated according to Eq. (4)
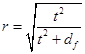 (4)
(4)
where “t” is the t-test “t” value and “df” is the degree of freedom.
IDL®, Version 8.4.0, a programming language from Exelis Visual Information Solutions, Boulder, Colorado, USA was used for the lung segmentation, the estimates of the morphometric parameters, and the statistics calculations. The used license included the IMSL statistics library.
Table 1 summarizes the mean values, standard deviations, and p values of the morphometric parameters, “volume,” “densitometry,” and “D,” each before and after smoke inhalation, for the set containing the complete HU-range L[-1000, 399]. The p values support the assumption on a 0.05 significance level that the groups “before” and “after” smoke inhalation can be distinguished by volumetric analysis, while this assumption is not supported here by densitometry or fractal analysis.
Figure 5 shows the mean values and the standard deviation of the morphometric parameters “volume,” “densitometry,” and “D,” estimated for the 28 different, consecutive HU-ranges that were used to define the subsets beginning from [-1000,-949] up to the radiologically densest range of [350,399] HU. Results are shown for the groups “before” and “after” smoke inhalation. A logarithmic scale was chosen for “volume” and “density” so that variations in small volumes or densities are still visible.
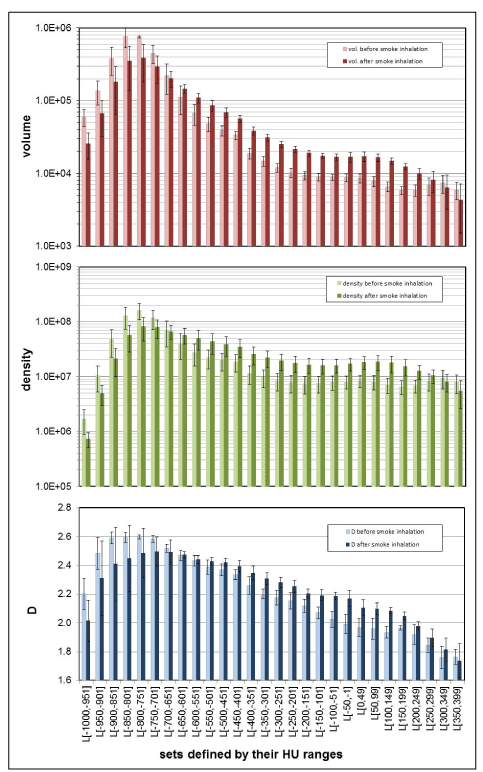
Figure 5. The group averages for lung subsets examined “before” and “after” smoke inhalation for volume estimates in units of [mm3], densitometry in [HU], and fractal D. The results are shown along with their standard deviations. Each of the three parameters were estimated from a subset that was defined by a specific HU-range L [HU-range], given on the x-axis.
Figure 6 shows the p-values as a function of the different HU subset ranges, calculated with the t-test, for the group comparisons “before” and “after” smoke inhalation, for the parameters “volume,” “densitometry,” and “D”. The Shapiro-Wilk test indicated that it is reasonable to assume that the data is distributed normally, and the f-test indicated that variances are homogenous for all groups compared by the t-test that had p values ≤ 0.05. The Shapiro-Wilk and f-test were calculated at a 0.05 significance level each. In addition to the p values, the effect size, r, for all parameters shown in Table 1 and Figure 6 were calculated. The average, r, of the group comparisons with p ≤ 0.05, was 0.93 for the volumetric investigation, and 0.95 for each of the density and the fractal analysis group comparisons. The p values indicate that group differentiations were possible for many different HU subset ranges by all three morphological parameters.
Table 1. Morphometric analysis of the complete HU-range [-1000, 399].
| Statistic parameter |
volume analysis |
densitometry |
fractal dimension |
| mean value before |
3.2 ± 0.2 l |
7.94E+08 ± 2.52E+08 HU |
2.70 ± 0.03 |
| smoke inhalation |
| |
|
|
| mean value after |
2.2 ± 0.7 l |
7.86E+08 ± 1.40E+08 HU |
2.61 ± 0.05 |
| smoke inhalation |
| |
|
|
| p value (paired t-test) |
0.05 | 2021 Copyright OAT. All rights reserv
0.945 |
0.196 |
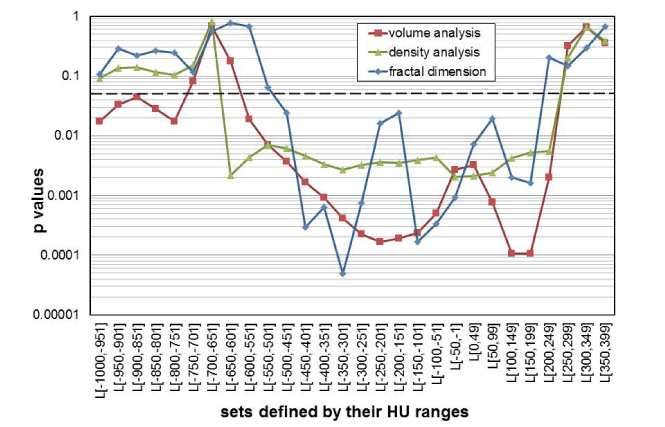
Figure 6. Diagram of p-values that were calculated by paired t-tests comparing the mean values of the groups “before” versus “after” smoke inhalation for each of the parameters: volume (red line), density (green), and fractal D (blue); the 0.05 significance limit is shown as a dot-ted line. The corresponding mean values and standard deviations for each parameter are given in Figure 5.
Discussion of the results of this study
In this investigation, the p value was used as a principal parameter to differentiate whether group discrimination could be assumed or not. As recommended by Bland and Altman [17] to test for group differences in small sample sizes, a paired t-test was used to calculate p. Since the effect size found in this investigation is in the order of at least 0.93 in all group comparisons with p ≤ 0.05, one may conclude that the interpretation of p is unambiguous despite the small group size of only 5 animals.
The p values in Table 1 suggest that only volumetric analysis supports the assumption that a significant differentiation between the groups “before” and “after” smoke inhalation is possible within a significance limit of 0.05, when the complete set L[-1000,399] is analyzed. This behavior is very different if one looks at the p values obtained in the group comparisons for the sets that cover a HU-range of only 50 HU width. Here, many different HU subset ranges support the assumption that group differentiations are possible by all three morphological parameters, “volume,” “densitometry,” and “D.” Therefore, in answer to the first question in the introduction, successful group differentiation can be assumed for all three of the investigated parameters.
The second question was whether all three of the investigated image analysis methods are equally good in respect to their ability to allow successful group differentiations. Looking at the statistics of correctly true positive group differentiations, one finds that 22 out of 28 HU subranges were correctly identified by the volume analysis (79%) method; 18 of 28, by the density analysis (64%) method; and 15 out of 28, by the fractal dimension analysis (54%) method. If one accepts this ranking method, it would seem that volumetric analysis is superior to the density analysis and fractal analysis methods, which are both basically identical in respect to their ability to differentiate groups. But if one raises the p significance limit from 0.05 to 0.001, to assume that a group differentiation is possible, only the volumetric and the fractal analysis method support the assumption that groups can be discriminated (Figure 6). Both of these methods are, therefore, superior to density analysis. And if one were to reject all results with p ≥ 0.0001, only the fractal analysis method would support the assumption that one HU subset can be successfully differentiated from another.
The third question was whether it is reasonable to analyze many small subsets of limited HU-range, rather than analyzing just one very large HU-range. The results in Figure 6 indicate that it is, indeed, advisable to investigate many smaller HU-ranges to explore group differentiations. Methods like density analysis or D analysis, which prove successful when small HU sub-ranges are studied, might, otherwise, be falsely considered useless. This sub-range approach to data analysis is similar to the one radiologists use when they specifically select window and level settings to visualize peculiarities in a CT data set. Our findings in this respect are also in agreement with the empiric knowledge in radiology that a falsely chosen window level may preclude a correct radiological diagnosis. This new insight can presumably also be applied to other investigations, in which the correlation between different diseases, or severities of a disease, and the morphological parameters “volume,” “densitometry,” or “D” are being explored. This is supported by further arguments given in the next paragraphs.
Plausibility of the results
The behavior of the HU subset ranges with low radiation attenuation, beginning from L[-1000,-951] to approximately L[-700,-651], is plausible. Prior to smoke inhalation, the lung volume is much larger. The lung density exhibits similar behavior, due to the fact that many more voxels with low attenuation HU exist prior to the inhalation event, and the term “density” was defined as the sum of all HU of all existing voxels in a set, see Equation 2. The fractal dimension is also larger prior to the smoke inhalation event than afterwards. This is the same result that one finds when one looks at the D values from the analysis of the complete lung sets L[-1000,399] shown in Table 1. Hence, D can, again, be understood as a measure of the ability to fill a space and it, to a certain degree, follows the volume behavior. The interpretation of the fractal dimension is, actually, more complicated than the density or the volume parameters. This is because the fractal dimension incorporates geometrical properties as well as properties that are related to the density of the investigated structure. If D were to reflect volume only, the fractal dimension spectrum in Figure 5 would be identical with the volume spectrum in the graph. On the other hand, if D were to reflect density only, the fractal dimension spectrum in Figure 5 would be identical with the density spectrum. Instead, one finds that these spectra are different. Hence, the fractal spectrum contains additional information that may be relevant, for instance, to distinguish different experimental groups from each other.
Discussion of methodologies of this study
The segmentation process of the CT images “before” and “after” smoke inhalation that was fundamental to this numerical investigation was guided by the low radiation attenuation of lung tissue that contains air. For the healthy lung, this segmentation approach agrees completely with the anatomical definition of the lung shape defined as the lower respiratory sys-tem. By contrast, very radiologically dense areas in the smoke-affected lung are not completely segmented (Figure 1). Such missing regions may have HU values that are as dense as heart tissue. Although our segmentations of the smoke-affected lungs were partially incomplete, the segmentation approach was considered entirely satisfactory, as it allowed a significant differentiation between the two experimental groups by various morphometric parameters. In this pragmatic approach, this was all that was desired. Moreover, it is interest-ng to note that a group differentiation could, in particular, be achieved in the denser HU value ranges, beginning roughly with subsets at L[-550,-501] and denser. This indicates that enough of the denser tissue was segmented to make group differentiations possible. In these dense subsets, the volume was larger after smoke inhalation than before the inhalation procedure. At first, this finding is astonishing, given that the average complete volume of the lung decreased dramatically after smoke inhalation, see Table 1, but, with the volume data in mind, it is easy to understand the density behavior in the denser HU subset ranges: Since a larger volume of voxels with higher density can be found after smoke inhalation, the density necessarily also increases after smoke inhalation compared to the density before smoke in-halation (Figure 5). The fractal dimension spectrum of the denser HU subsets in Figure 5 can be understood when one considers the volume and density properties within these sub- set ranges: The volume and the density increase after smoke inhalation compared to the status before the inhalation event. Since the fractal dimension is, in a certain way, a measure of the space-filling ability of a geometrical set, see Figure 4, the fractal dimension also increases after the smoke inhalation event.
Advantage of analysis of animal experiments
Prior to a clinical application, numerical image analysis methods must be thoroughly tested and well understood so that radiologists and patients can assess and trust their outcome. The easier it is to predict a diagnosis, the easier it is to assess methods that lead to that diagnosis. Numerical image analysis tools can be assessed in animal experiments in which an effect that has been purposely induced leads to a well-defined morphological change and causes group differences “before” and “after” the induced effect. An approach such as this was, for example, chosen by Obert et al., who studied asthma attacks induced by methacholine in mice in an acute asthma mouse-model [11]. The morphology of the lung “before” and “after” the attack was monitored with an experimental high-resolution flat-panel computed tomography system and also confirmed histologically. The resulting CT image data, which were perfectly designed for the study of computer-aided diagnosis (CAD) projects, could then be viewed as an “in vivo phantom.” In the study, Obert et al. successfully applied the concept of fractal geometry. The fractal dimension, which serves as a measure to de-scribe the irregularity or the complexity of a geometrical set, was used to discriminate be-tween the different lung morphologies.
Examples of other fractal lung investigations
Gupta et al. investigated 65 patients suffering from asthma and compared them with 30 healthy volunteers by estimating changes in lung volume and by determining the fractal dimensions of segmented airway trees [18]. They found a significant reduction in volume and fractal dimension in asthmatics and concluded that this was a novel method with which to differentiate between different asthma phenotypes.
When Copley et al. analyzed CT images, they found that the fractal dimension and the mean lung density decrease in non-smoking urban-dwelling older subjects compared to younger subjects [19].
Michallek and Dewey reported, in a review, that fractal characterizations were successfully applied to perfusion imaging of tumors of the lung, myocardium, kidney, skeletal muscle, as well as to the imaging of cerebral diseases [20].
In the literature, one can often read that the fractal dimension is a measure of the complexity of a system [21]. In this context, “complexity” is directly related to the fractal dimension, and the higher this value, the higher the said complexity of this system is. Many other investigations also show that a healthy system has a higher complexity, or larger fractal dimension value, than the diseased state. Boser et al., for example, evaluated silicon rubber casts of the human lung and found a significant difference between a healthy control group (D = 1.83) and patients suffering from asthma (D = 1.76) [22]. And Moledina et al. performed a fractal image analysis of skeletonized artery vessels that were segmented from the lung at different disease states of pulmonary hypertension [23]. The mild form had a D of 1.66, the moderate form had a D of 1.48, and the severe form had a D of only 1.27. An in-depth discussion of the theoretical background and meaning of D is beyond the scope of this article and can be found in the literature.
What are the next steps?
CAD methods definitely need to be able to do more than to be able to provide support for the distinction of “before” or “after” a smoke inhalation injury, as in this study. This information on its own would be completely trivial for radiologists. Useful CAD systems have to be able to help differentiate between many different diseases and categories of severity of a disease. In future investigations, the data from human patients should, therefore, be studied in this regard. The paired t-test could then be replaced by advanced classification methods like contingency table analysis, Bayesian classifiers (BC), support vector machines (SVM), or neuronal networks [24]. That this can be successfully applied, in principle, was shown by Xu and colleagues in 2006 [25]. They combined volumetric results, HU histogram data, and fractal dimension values from regions of interest for 20 patients with different lung diseases and used BC and SVM algorithms to perform classifications with a specificity and sensitivity of sometimes above 90%. With further detailed geometrical statistics, as from this investigation, it will hopefully be possible to improve the specificity and sensitivity of these classification methods.
In this study, which evaluated geometrical sets from CT image data, volume, density and fractal properties were compared “before” and “after” a severe event that changed the morphology of the lung. When the entire HU-range of the sets was analyzed, a significant group differentiation was feasible only with the volume analysis method. When the complete HU-range was divided into many separately analyzed small subsets, a spectrum that enabled a significant differentiation into groups “before” and “after” the inhalation event was obtained for each of the morphological parameters, “volume,” “density,” and “D.” As a function of the HU-separation range, each spectrum had its own, different behavior and, therefore, contained individual information not contained in the other spectra. To the best of our knowledge, this has never been shown in such detail in the literature so far. It is, thus, useful to investigate many small HU subranges rather than only one large HU-range. Furthermore, it is reasonable to investigate all three morphometric parameters individually, since they each provide specific information that can contribute to a more complete overview picture. Detailed knowledge of the properties of such morphometric parameters is fundamental to their successful application in automated image analysis projects and CAD.
Clinical relevance
- Although new and modern imaging techniques provide high-resolution images of all parts of the body, interpretation of the images remains very subjective and is highly dependent on the skills and the experience of the radiologist.
- Automated image analysis could introduce a major change in radiology by generating objective parameters that can simplify diagnosis for radiologists.
- An approach similar to that used in radiological diagnostics, in which “window width” and “window level” settings are carefully selected, was applied to the numerical anal-ysis of CT data sets in this study and enabled a significant differentiation between phenotype groups with densitometry and fractal methodology. This differentiation was otherwise only possible with volume analysis.
We thank Dr. Johannes Herrmann for helpful discussions concerning the statistics and Diana Neumann for her help in the preparation of the manuscript.
- Dinkel J, Khalilzadeh O, Hintze C, Fabel M, Puderbach M, et al. (2013) Inter-observer reproducibility of semi-automatic tumor diameter measurement and volumetric analysis in patients with lung cancer. Lung Cancer 82: 76-82. [Crossref]
- Wulff AM, Bolte H, Fischer S, Freitag-Wolf S, Soza G, et al. (2012) Lung, liver and lymph node metastases in follow-up MSCT: Comprehensive volumetric assessment of lesion size changes. Fortschr Röntgenstr 184: 820–828. [Crossref]
- Wang R, Sui X, Schoepf UJ, Song W, Xue H, et al. (2015) Ultralow-radiation-dose chest CT: accuracy for lung densitometry and emphysema detection. AJR Am J Roentgenol 204: 743-749. [Crossref]
- Rubenfeld GD1, Caldwell E, Peabody E, Weaver J, Martin DP, et al. (2005) Incidence and outcomes of acute lung injury. N Engl J Med 353: 1685-1693. [Crossref]
- Brigham PA, McLoughlin E (1996) Burn incidence and medical care use in the United States: estimates, trends, and data sources. J Burn Care Rehabil 17: 95-107. [Crossref]
- Lundy JB, Chung KK, Pamplin JC, Ainsworth CR, Jeng JC, et al. (2016) Update on Severe Burn Management for the Intensivist. J Intensive Care Med 31: 499-510. [Crossref]
- Herndon DN, Traber DL, Niehaus GD, Linares HA, Traber LD (1984) The pathophysiology of smoke inhalation injury in a sheep model. J Trauma 24: 1044-1051. [Crossref]
- Zhou X, Hayashi T, Hara T, Fujita H, Yokoyama R, et al. (2006) Automatic segmentation and recognition of anatomical lung structures from high-resolution chest CT images. Comput Med Imaging Graph 30: 299-313. [Crossref]
- Kakar M, Olsen DR (2009) Automatic segmentation and recognition of lungs and lesion from CT scans of thorax. Comput Med Imaging Graph 33: 72-82. [Crossref]
- Nakagomi K, Shimizu A, Kobatake H, Yakami M, Fujimoto K, et al. (2013) Multi-shape graph cuts with neighbor prior constraints and its application to lung segmentation from a chest CT volume. Med Image Anal 17: 62-77. [Crossref]
- Obert M, Hagner S, Krombach GA, Inan S, Renz H (2015) Fractal geometry enables classification of differ-ent lung morphologies in a model of experimental asthma. Fractals 23.
- Obert M, Seyfried M, Schumacher F, Krombach GA3, Verhoff MA, et al. (2014) Aging adult skull vaults by applying the concept of fractal geometry to high-resolution computed tomography images. Forensic Sci Int 242: 24-31. [Crossref]
- Mandelbrot BB (1982) The fractal geometry of nature. San Francisco: Freeman.
- Pfeifer P, Obert M (1989) Fractals: Basic concepts and terminology. In: Avnir D (Ed), The fractal approach to heterogeneous chemistry. Chichester: John Whiley & Sons, 11-43.
- Obert M (1993) Numerical estimates of the fractal dimension D and the lacunarity L by the mass radius relation. Fractals 3: 711-721.
- Ahammer H, DeVaney TTJ, Tritthart HA (2003) How much resolution is enough? Influence of downscaling the pixel resolution of digital images on the generalized dimensions. Physica D 181: 147-56.
- Bland JM, Altman DG (2009) Analysis of continuous data from small samples. BMJ 338: a3166. [Crossref]
- Gupta S, Hartley R, Khan UT, Singapuri A, Hargadon B, et al. (2014) Quantitative computed tomography–derived clusters: Redefining airway remodeling in asthmatic patients. J Allergy Clin Immunol 133: 729-738. [Crossref]
- Copley SJ, Giannarou S, Schmid VJ, Hansell DM, Wells AU, et al. (2012) Effect of aging on lung structure in vivo: assessment with densitometric and fractal analysis of high-resolution computed tomography data. J Thorac Imaging 27: 366-371. [Crossref]
- Michallek F, Dewey M (2014) Fractal analysis in radiological and nuclear medicine perfusion imaging: a systematic review. Eur Radiol 24: 60-69. [Crossref]
- Andersen MP, Parham AR, Waldrep JC, McKenzie WN, Dhand R (2012) Alveolar fractal box dimension inversely correlates with mean linear intercept in mice with elastase-induced emphysema. Int J Chron Obstruct Pulmon Dis 7: 235–243. [Crossref]
- Boser SR, Park H, Perry SF, Ménache MG, Green FH (2005) Fractal geometry of airway remodeling in human asthma. Am J Respir Crit Care Med 172: 817-823. [Crossref]
- Moledina S, de Bruyn A, Schievano S, Owens CM, Young C, et al. (2011) Fractal branching quantifies vascular changes and predicts survival in pulmonary hypertension: a proof of principle study. Heart 97: 1245-1249.
- Gao X, Chu C, Li Y, Lu P, Wang W, et al. The method and efficacy of support vector machine classifiers basedon texture features and multi-resolution histogram from18F-FDGPET-CT images for the evaluation of mediastinal lymph nodes inpatients with lung cancer. Eur J Radiol 84: 312–317.
- Xu Y, van Beek EJ, Hwanjo Y, Guo J, McLennan G, et al. (2006) Computer-aided classification of interstitial lung diseases via MDCT: 3D adaptive multiple feature method (3D AMFM). Acad Radiol 13: 969-978. [Crossref]



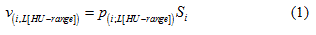
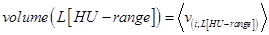 , where 〈 . 〉 denotes the average volume of the 5 sheep, each estimated for their specified HU-range.
, where 〈 . 〉 denotes the average volume of the 5 sheep, each estimated for their specified HU-range.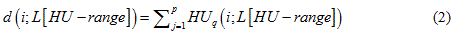
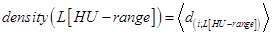 , where 〈 . 〉 denotes the average density of the 5 sheep, each at their specified HU-range.
, where 〈 . 〉 denotes the average density of the 5 sheep, each at their specified HU-range.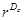 :
: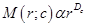 (3)
(3)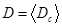 , where 〈 . 〉 denotes the average of 100 counting results for different center positions, c. The regression ranges, within which the linear regression is calculated to obtain D in such plots, were always chosen to be the same to allow a comparison of D-values from different animals and experimental groups.
, where 〈 . 〉 denotes the average of 100 counting results for different center positions, c. The regression ranges, within which the linear regression is calculated to obtain D in such plots, were always chosen to be the same to allow a comparison of D-values from different animals and experimental groups.

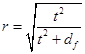 (4)
(4)
