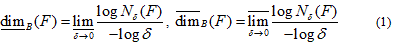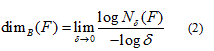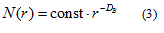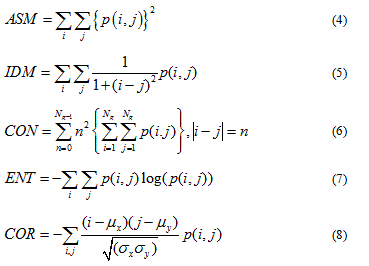All cells in the human organism, including stem cells, have a limited lifespan and cease to divide after a certain number of divisions. The process of cellular senescence refers to incapability to progress through the cell cycle, thus leading the cell to an irreversible growth arrest. One of the most common biomarkers of cell senescence is senescence-associated β-galactosidase (SA-β-Gal/SABG), a lysosomal enzyme detectable at pH = 6.0. However, the proper identification of senescent cells is still insufficient and lacks adequate quantification parameters. In this paper we showed that fractal and gray level co-occurrence matrix (GLCM) texture analysis of cell nuclei are able to discriminate senescent from non-senescent cells. A total of 105 images of DTSCs nuclei from both SA-β-Gal+ and SA-β-Gal- cells were used in this study. All of the computed parameters (fractal dimension, angular second moment, inverse difference moment, contrast, entropy and correlation) showed significant statistical difference between the nuclei of senescent and non-senescent stem cells (p < 0.001). Our results show the possible practical value of fractal and GLCM texture analysis as the new markers in the determination and quantification of DTSCs senescence.
nucleus, chromatin, complexity, shape, aging
Dental pulp stem cells (DPSCs) represent a heterogeneous population of multipotent stem cells that have the ability to differentiate into various types of cells [1]. Since they can be easily obtained from teeth during routine dental procedures, especially DPSCs from human deciduous teeth (also known as deciduous teeth stem cells, DTSCs), have gained a very large attention in recent years from a potential therapeutic standpoint [2].
All cells, including stem cells, have a limited lifespan. After a certain number of divisions, stem cells are subjected to aging, which is characterized by different morphofunctional parameters. One of those changes is the accumulation of lysosomal enzyme β-galactosidase at pH = 6.0 (senescence-associated β-galactosidase/SA-β-Gal/SABG), whose activity is associated with cell senescence in vitro [3,4]. The process of cellular senescence refers to irreversible growth arrest, which is followed by changes in nuclear factors [5]. Although SA-β-Gal is widely used as a biomarker for detecting aging and senescence in stem cells in vitro [6], the proper identification of senescent cells is still insufficient and cell-based methods for identification of those cells are not quantitative [7].
Fractal analysis is a method used to measure the complexity of an object. It is widely used in several different areas of biological and medical sciences, such as neuroscience [8-11], histological diagnosis and quantification of neoplasms [12-15], blood vessels changes [16,17], assessment of cell aging [18] and many others. New methods and modifications of fractal analysis are also being discovered [19], thus allowing this mathematical method to be applied in different areas of natural sciences. Unlike fractal analysis, gray level co-occurrence matrix (GLCM) texture analysis can be used in biomedical research to analyze texture features of histological images and also to quantify structural changes in cells and tissues [20,21].
Based on this background, our idea was to determine whether fractal and GLCM texture analysis of DTSCs nuclei could prove as a useful tool in the detection and quantification of stem cell senescence in vitro.
Deciduous teeth stem cells isolation
Deciduous teeth stem cells were isolated from a healthy deciduous maxillary central incisor obtained from a 7 year old child. The tooth extraction was done with informed consent of its parents and ethical comity approval. Pulp tissue was minced into 1–2 mm fragments, transferred to 35 mm Petri dishes and cultivated using Dulbecco’s modified Eagle’s medium (DMEM) / Ham’s F12 (1:1, Invitrogen, Carlsbad, California, USA) supplemented with 10% FBS MSC qualified (Invitrogen, Carlsbad, California, USA) and AA solution, and incubated at standard conditions (37°C, 5% CO2). The DTSCs used for this experiment were from passage number four. Additional experimental information about dental pulp and stem cell isolation can be found in Martacić et al. [22].
Senescence-associated β-galactosidase activity
Senescence-associated β-galactosidase activity was determined by using a commercial kit (Senescence Cells Histochemical Staining Kit – Sigma-Aldrich) according to the manufacturer's instructions. Approximately around 2.5 x 104 DTSCs were cultured in each well (Multiwell Glass Chamber Slides, BD Biosciences) during 24 hours, after which they were washed in PBS, fixed with a 4% formaldehyde for 5 minutes at room temperature and then incubated at 37°C overnight in a freshly prepared staining solution containing X-Gal (5-Bromo-4-chloro-3-indolyl β-D-galactoside) at pH = 6.0. After washing in PBS, the cells were counterstained with Mayer’s hematoxylin for better visualization of nuclei. The SA-β-Gal positive (SA-β-Gal+) and negative (SA-β-Gal-) cells are shown in Figure 1.
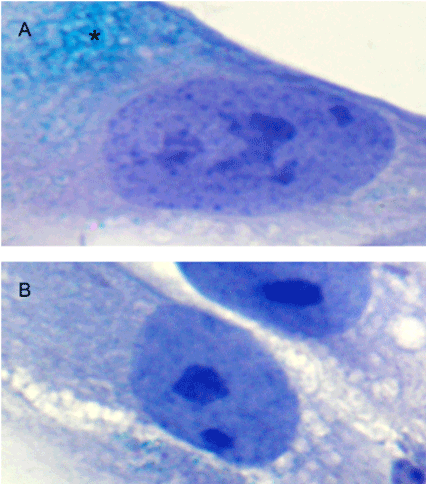
Figure 1. SA-β-Gal staining in DTSCs. A – Microphotograph of SA-β-Gal+ cell with characteristic greenish-blue accumulations in the cytoplasm (*), indicating cell senescence. B – An example of SA-β-Gal-cell, i.e. non-senescent cell (magnification x1000).
Acquisition and graphic processing of images
For fractal and GLCM texture analysis of DTSCs nuclei, digital photos were taken with an Olympus digital camera (Olympus C5060-ADU) and analySIS 5.0 software (Soft Imaging System, Olympus) at x1000 magnification with immersion. The images were saved in TIFF format with a dimension of 2592 x 1944 pixels, resolution of 200 DPI and bit depth of 24. All picture elements, except the nucleus itself, were removed. Also, in order to avoid the influence of rotational variations on the value of fractal dimension (FD) all nuclei were placed centrally and rotated so that their longer axis was parallel to x axis (Figures 2A and 2E). After this graphic processing, a total of 105 images containing a single nuclei per picture (obtained from 55 SA-β-Gal+ and 50 SA-β-Gal- cells), were used for further fractal and GLCM texture analysis.
Fractal analysis using the box-counting method
The lower and upper box-dimensions of a subset 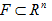 are respectively defined by
are respectively defined by
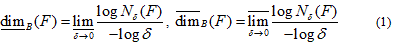
and if those values are equal then the common value is referred to as the box-counting dimension of F and is denoted by
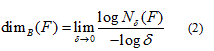
where Nδ(F) can be the smallest number of closed balls of radius δ that cover F, the smallest number of cubes of side δ that cover F, the number of δ-mesh cubes that intersect F, the smallest number of sets of diameter at most δ that cover F or the largest number of disjoint balls of radius δ with centers in F [23]. The box-counting method, applied on digitized images, covers the image with a grid of square cells (with cell size r), where for binary images the cell size is expressed as the number of pixels. The number of squares N(r) needed to cover the image is given by a power law
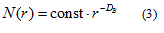
where DB is the box dimension, obtained as an absolute value of the slope of the log-log relationship between N(r) and r [24].
Image processing and fractal analysis were carried out in the ImageJ 1.48v software (NIH, Bethesda, USA; free download from http://rsbweb.nih.gov/ij). We calculated two forms of FD: the FD of the “binary-outlined” nucleus (Dout), which measures the shape of an image (Figures 2C and 2G) and the FD of the corresponding “black-and-white” image (Dbin), which evaluates the space-filling property of an image (Figures 2D and 2H).
In order to calculate Dout, firstly the images were converted to an 8-bit format (pathway: ImageJ>Image>Type>8-bit), followed by the Find Edges command in order to outline the nucleus (pathway: ImageJ>Process>Find Edges) and then finally transformed to a binary format (pathway: ImageJ>Process>Binary>Make binary) and skeletonized (pathway: ImageJ>Process>Binary>Skeletonize) (Figure 2). The same procedure was used to calculate Dbin, but with an addition of the Fil command after the binarization process, which in this case, represented the last step in the process of image transformation (Figures 2D and 2H)
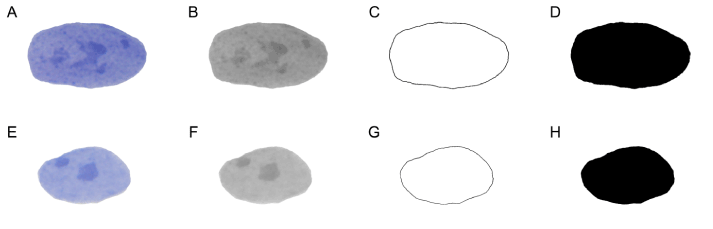
Figure 2. Graphic processing of cell nuclei. The first row represents the steps in the graphic processing and analysis of SA-β-Gal+ cell nuclei (images A to D), while the second row represents the same steps applied to the nuclei of SA-β-Gal- cells (images E to H). A, E – all of the nuclei were positioned centrally and rotated in the same order to avoid the rotational variations which can influence the value of fractal dimension. B, F – grayscale nuclei images used for texture analysis. C, G – images of the “binary-outlined” nuclei, on whom the skeletonization process was applied in order to calculate Dout. The skeletonized images are not shown in this figure, due to the small thickness (1 pixel) of the line. D, H - “black-and-white” images of the same nuclei used for calculating Dbin.
The fractal analysis was done using the box-counting method (pathway: ImageJ>Analyze>Tools>Fractal Box Count). By default, the box sizes for counting the fractal dimension using the ImageJ software are 2, 3, 4, 6, 8, 12, 16, 32, 64. In this paper, the box sizes were 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, obtained as an increasing geometric progression 2n where n = 0, 1, 2…10, as also used in our previous papers [9,19].
Gray level co-occurrence matrix texture analysis
In order to calculate GLCM parameters of DTSCs nuclei, an ImageJ plugin called “Texture Analyzer” version 0.4 was applied (http://rsb.info.nih.gov/ij/plugins/texture.html; developed by Julio E. Cabrera). The analysis was performed on grayscale 8-bit images (Fig. 2B, 2F), with the size of the step in pixels set to 1 and the direction of the step set to 0°. The following five parameters were computed: angular second moment (ASM), inverse difference moment (IDM), contrast (CON), entropy (ENT) and correlation (COR) by following formulas:
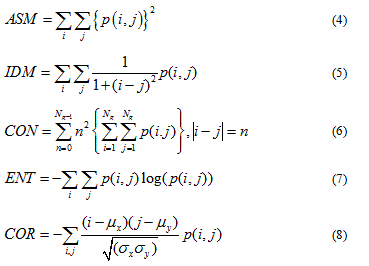
The term p(i,j) is the ith and jth entry in a normalized gray-tone spatial-dependence matrix (i.e. the co-occurrence matrix) and Ng is the number of distinct gray levels in the quantized image. The above mentioned formulas, originaly described by Haralick et al. [25] are implemented in the “Texture Analyzer” Image J plugin. The only parameter computed differently is COR, which is calculated as described by Walker et al. [26]. Texture analysis aims to indentify texture features of object in an image by analyzing combinations of intensities at specified positions that are relative to each other in the image [27]. Statistical texture analysis can therefore be classified into first-order, second-order and higher-order statistics according to the number of intensity points (pixels) in each combination. The GLCM texture analysis aims to describe the second order texture features [27]. Originaly Harlick et al., [25] described a total of 14 statistical texture measures that are based on gray tone spatial dependencies. From those 14 parameters, 5 parameters are commonly used in biomedical research for image classification purposes [25]. ASM, also known as, Energy and IDM, also known as Homogeneity, are measures of image homogeneity. High ASM and IDM values are thus present when the image is made of pixels with very similar gray level values, which points to the texture that is uniform and contains repetitive structures [28]. CON and ENT are measures of image heterogeneity, and represent measures of gray level variation and spatial disorder. High CON values can be found in heavy textures images, while high ENT indicates that the image texture is statistically more chaotic [28]. COR is a measure of gray level linear dependence between the pixels at the specified positions relative to each other [27].
Statistical analysis
Statistical analysis was performed using Student's t test and Mann-Whitney’s U test, where appropriate. Results are represented as mean ± standard error of mean, and as median with interquartile range. For p values less than 0.05, the differences between the means of populations were considered statistically significant.
The fractal analysis of “binary-outlined” nucleus showed no statistical significance between two groups. On the other hand, the fractal analysis of “black-and-white” nucleus images showed significant statistical differences between two groups of cells (Table 1).
Table 1. The average fractal dimension of DTSCs “binary-outlined” and “black-and-white” nuclei obtained from SA-β-Gal- and SA-β-Gal+ groups.
Parameters |
Group |
t |
p |
SA-β-Gal- |
SA-β-Gal+ |
Dout |
1.083 ± 0.004 |
1.085 ± 0.002 |
0.613 |
0.542 |
Dbin |
1.811 ± 0.007 |
1.781 ± 0.005 |
3.595 |
< 0.001 |
*Results are represented as mean ± standard error of mean. Abbreviations: Dout – fractal dimension of the “binary-outlined” nucleus images; Dbin – fractal dimension of “black-and-white” nucleus images.
GLCM texture analysis showed high statistical significance in all of the five computed parameters (Table 2).
Table 2. Parameters of GLCM texture analysis of nuclei obtained from SA-β-Gal- and SA-β-Gal+ groups of DTSCs.
Parameter |
SA-β-Gal- |
SA-β-Gal+ |
U |
p |
ASM |
0.97772 (0.97457 – 0.98027) |
0.95598 (0.94166 – 0.96482) |
72.000 |
< 0.001 |
IDM |
0.99312 (0.99229 – 0.99413) |
0.9869 (0.9829 – 0.9899) |
77.500 |
< 0.001 |
CON |
25.2682 (25.2318 – 25.3017) |
25.3591 (25.2931 – 25.4938) |
640.000 |
< 0.001 |
ENT |
0.13293 (0.11421 – 0.14494) |
0.24854 (0.19733 – 0.31466) |
69.000 |
< 0.001 |
COR |
0.00941 (0.00751 – 0.01128) |
0.00614 (0.00432 – 0.00901) |
618.000 |
< 0.001 |
*Results are represented as median with interquartile range. Abbreviations: ASM – angular second moment; IDM – inverse difference moment; CON – contrast; ENT – entropy; COR – correlation.
Although standard quantitative methods in science are based on classical Euclidean geometry, early research showed that the most common biological patterns were characterized by fractal geometry [29,30]. Up to now the concept of fractal geometry is being used in diverse research areas and is proving to be an increasingly useful tool. In fractal analysis, a type of quantitative analysis derived from fractal geometry [31], there are two basic methods to measure the FD of objects in a plane: the first and most commonly used is a length-related method, while the second method is a mass-related method [29]. Although there are no strict guidelines for the application of fractal analysis, the majority of researches tend to use box-counting method to calculate the FD of digital images, making this method one of the most frequently used [31].
In our study the box-counting method of fractal analysis applied on nuclei of SA-β-Gal+ and SA-β-Gal- cells, i.e. senescent and non-senescent cells, gave two different types of results. The first result showed no statistical significance between the mean FD values of the “binary-outlined” nucleus, while the second result showed high statistical significance when fractal analysis was applied on “black-and-white” corresponding images of the nuclei. These contradictory results can be explained by the different parameters which were measured by these two methods. The first method, measured the shape of the nucleus, while the second method evaluated the space-filling property of an image of the nucleus. It has been reported previously [30] that the box-counting method applied on binary images of neurons depends on the way the image is displayed. While the box dimension of “binary-skeletonized” images summarizes the degree of dendrite aberrations from straight lines [32], the same parameter for “binary-outline” images defines the irregularity in the shape of the image. In addition, the box dimension of the “black-and-white” images represents a robust technique for estimating how the extent of the image deviates from the extent of the geometric figure, according to resolution [33]. Thus, according to our results, the fractal analysis of certain geometrical shapes, such as the shape of cell nuclei, should be done on “black-and-white” images, which in these conditions give more adequate results than the analysis on the “binary-outline” images.
The biological differences obtained in the values of nucleus FD in senescent and non-senescent cells on “black-and-white” images can be explained by changes that occur in the process of stem cell aging [4]. Namely, it was noticed that increase in whole cell size and nuclear size is often associated with senescence [34,35]. Also, abnormal nuclear morphology, such as irregular shape or fragmentation, is often seen in senescent cells [36]. Thus, it is not surprising that “black-and-white” nuclei images of SA-β-Gal+ senescent cells have lower values of FD than β-gal- cells, most likely due to the loss of their normal shape and structure. This result is in accordance with other researches that showed that with aging, FD of certain tissue decreases, thus pointing to the loss of structural complexity as a consequence of tissue age-related degradation and deterioration [18].
Besides fractal analysis, GLCM texture analysis has proven to be an even better method in detecting the stem cell senescence in vitro. In our research, all five computed GLCM parameters showed high statistical significance between two groups of cells. As mentioned earlier, ASM and IDM are two parameters that measure tissue homogeneity, whereas second two parameters, CON and ENT measure tissue heterogeneity [25]. Also, IDM relates inversely to CON, while ASM is an opposite of ENT. COR measures the grey-linear dependency of neighboring pixels, where high COR indicates greater pixel similarity and low COR points towards irregularity in image texture [37]. Our results showed that nuclei of SA-β-Gal+ cells, have higher values of ENT and CON than SA-β-Gal- cells, while ASM, IDM and COR of cell nuclei are higher in the SA-β-Gal- group. These results can be explained by the changes in the chromatin structure in senescent cells, whose nuclei show significant structural changes. The most prominent is formation of the senescence-associated heterochromatic foci [38]. Second is distorted organization of the nuclear lamina [5,39], such as downregulation of lamin B1 [40], which leads to the permeabilization of the nuclear envelope. It causes a loss of chromatin from the nucleus to the cytoplasm, together with a progressive decrease in histone content [41]. In this way, the normal nuclear architectonic is lost, leading to an increase in pixel heterogeneity and decrease in pixel homogeneity, which can be detected by GLCM parameters of texture analysis, as it is shown by our results. These results are in accordance with Pantic et al. [42] who have shown an increase in nuclear ENT of hematopoietic erythroid cells with age.
To our knowledge, this is the first study to show the usefulness of fractal and GLCM texture analysis in the detection of stem cell senescence. Our study had certain limitations, due to which it can be considered as a pilot study. The main limitation is the number of biological specimens from which images of DTSCs nuclei were extracted. Although, stem cells were obtained from only one tooth, this is not uncommon in stem cell research, where different experimental procedures are often done on stem cells isolated from one tooth or patient [43-45]. Thus, the next research step could be the application of these two methods on a larger number of specimens and on different types of mesenchymal stem cells isolated from various tissues. Besides β-galactosidase staining, additional markers of stem cell senescence should be included in future studies to obtain the most accurate results about the application of these two mathematical methods in senescence quantification.
As shown in our research, fractal and GLCM texture analysis of cell nuclei have proven to be a useful method to quantify stem cell senescence. Besides theoretical, these results also have a practical value, as they may become a new marker for laboratory detection of stem cell senescence, since they are easy to apply and carry no financial cost. The possible role of these methods in future studies can be directed to discriminate stem cells from different passages, to study the effects of different factors on the nuclear complexity of various cell lines or as tool for detecting stem cell differentiation. Although still in the early phase of application, several studies have recently used fractal and GLCM texture analysis for the similar purpose [21,46]. If future studies confirm the validity of these methods, a possible next step in the process of application could be a development of automated software, which would be able to calculate fractal and GLCM texture parameters in real time, without previous image processing.
2021 Copyright OAT. All rights reserv
This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia, Contract No. 175061.
- Potdar PD, Jethmalani YD (2015) Human dental pulp stem cells: Applications in future regenerative medicine. World J Stem Cells 7: 839-851. [ Crossref]
- de Souza PV, Alves FBT, Costa Ayub CLS, de Miranda Soares MA, Gomes JR (2013) Human immature dental pulp stem cells (hIDPSCs), their application to cell therapy and bioengineering: an analysis by systematic revision of the last decade of literature. Anat Rec (Hoboken) 296: 1923–1928. [ Crossref]
- Severino J, Allen RG, Balin S, Balin A, Cristofalo VJ (2000) Is beta-galactosidase staining a marker of senescence in vitro and in vivo? Exp Cell Res 257: 162-171. [Crossref]
- Sethe S, Scutt A, Stolzing A (2006) Aging of mesenchymal stem cells. Ageing Res Rev 5: 91-116. [Crossref]
- Raz V, Vermolen BJ, Garini Y, Onderwater JJ, Mommaas-Kienhuis MA, et al. (2008) The nuclear lamina promotes telomere aggregation and centromere peripheral localization during senescence of human mesenchymal stem cells. J Cell Sci 121: 4018–4028. [Crossref]
- Lee BY, Han JA, Im JS, Morrone A, Johung K, et al. (2006) Senescence-associated beta-galactosidase is lysosomal beta-galactosidase. Aging Cell 5: 187-195. [Crossref]
- Righolt CH1, van’t Hoff ML, Vermolen BJ, Young IT, Raz V (2011) Robust nuclear lamina-based cell classification of aging and senescent cells. Aging (Albany NY) 3: 1192-1201. [Crossref]
- Di Ieva A, Grizzi F, Jelinek H, Pellionisz AJ, Losa GA (2014) Fractals in the Neurosciences, Part I: General Principles and Basic Neurosciences. Neuroscientist 20: 403-417. [Crossref]
- Puškaš N, Zaletel I, Stefanovic BD, Ristanovic D (2015) Fractal dimension of apical dendritic arborization differs in the superficial and the deep pyramidal neurons of the rat cerebral neocortex. Neurosci Lett 589: 88–91. [Crossref]
- Grbatinic I, Maric DL, Milosevic NT (2015) Neurons from the adult human dentate nucleus: neural networks in the neuron classification. J Theor Biol 370: 11-20. [Crossref]
- Pantic I, Basailovic M, Paunovic J, Pantic S (2015) Relationship between chromatin complexity and nuclear envelope circularity in hippocampal pyramidal neurons. Chaos, Solitons & Fractals 76: 271–277.
- Tambasco M, Costello BM, Kouznetsov A, Yau A, Magliocco AM (2009) Quantifying the architectural complexity of microscopic images of histology specimens. Micron 40: 486–494. [Crossref]
- de Arruda PF, Gatti M, Facio FN Jr, de Arruda JG, Moreira RD, et al. (2013) Quantification of fractal dimension and Shannon's entropy in histological diagnosis of prostate cancer. BMC Clin Pathol 13: 6. [Crossref]
- Fabrizii M, Moinfar F, Jelinek HF, Karperien A, Ahammer H (2014) Fractal analysis of cervical intraepithelial neoplasia. PLoS One 9: e108457. [Crossref]
- Lee LH, Tambasco M, Otsuka S, Wright A, Klimowicz A, et al. (2014) Digital differentiation of non-small cell carcinomas of the lung by the fractal dimension of their epithelial architecture. Micron 67: 125–131. [Crossref]
- Helmberger M, Pienn M, Urschler M, Kullnig P, Stollberger R, et al. (2014) Quantification of tortuosity and fractal dimension of the lung vessels in pulmonary hypertension patients. PLoS One 9: e87515. [Crossref]
- Cavallari M, Falco T, Frontali M, Romano S, Bagnato F, et al. (2011) Fractal analysis reveals reduced complexity of retinal vessels in CADASIL. PLoS One 6: e19150. [Crossref]
- Pantic I, Paunovic J, Basta-Jovanovic G, Perovic M, Pantic S, et al. (2013) Age-related reduction of structural complexity in spleen hematopoietic tissue architecture in mice. Exp Gerontol 48: 926–932. [Crossref]
- Zaletel I, Ristanovic D, Stefanovic BD, Puskas N (2015) Modified Richardson's method versus the box-counting method in neuroscience. J Neurosci Methods 242: 93-96. [Crossref]
- Pantic I, Dacic S, Brkic P, Lavrnja I, Pantic S, et al. (2014) Application of fractal and grey level co-occurrence matrix analysis in evaluation of brain corpus callosum and cingulum architecture. Microsc Microanal 20: 1373–1381. [Crossref]
- Park SH, Shin JW, Kang YG, Hyun JS, Oh MJ, et al. (2014) Texture analyses show synergetic effects of biomechanical and biochemical stimulation on mesenchymal stem cell differentiation into early phase osteoblasts. Microsc Microanal 20: 219–227. [Crossref]
- Martacic JD, Francuski J, Luzajic T, Vukovic N, Mojsilovic S, et al. (2014) Characterization of deciduous teeth stem cells isolated from crown dental pulp. Vojnosanit Pregl 71: 735-741. [Crossref]
- Falconer K (2003) Fractal geometry: Mathematical Foundation and Applications, (2ndedn), UK: John Wiley & Sons.
- Milosevic NT, Ristanovic D, Jelinek HF, Rajkovic K (2009) Quantitative analysis of dendritic morphology of the α and δ retinal ganglion cells in the rat: a cell classification study. J Theor Biol 259: 142–150. [Crossref]
- Haralick R, Shanmugam K, Dinstein IH (1973) Textural features for image classification. IEEE Trans Syst Man Cybern 3: 610–621.
- Walker RF, Jackway P, Longstaff ID (1995) Improving Co-Occurrence Matrix Feature Discrimination. Proceedings of the 3rd Conference on Digital Image Computing: Techniques and Applications, Brisbane, Australia: 643–648.
- Albregsten F (1995) Statistical Texture Measures Computed from Gray Level Cooccurrence Matrices. Technical Note. Department of Informatics, University of Oslo, Norway.
- Gebejes A, Huertas R (2013) Texture characterization based on grey-level co-occurrence matrix. Faculty of Management Science and Informatics at the University of Žilina. 2nd Information and Communication Technologies-International Conference ICTIC. Žilina, Slovakia: 375–378.
- Smith TG Jr, Lange GD, Marks WB (1996) Fractal methods and results in cellular morphology--dimensions, lacunarity and multifractals. J Neurosci Methods 69: 123-136. [Crossref]
- Fernández E1, Jelinek HF (2001) Use of fractal theory in neuroscience: methods, advantages, and potential problems. Methods 24: 309-321. [Crossref]
- Miloševic NT, Krstonosic B, Elston GN, Rajkovic N. (2013) Box-count analysis of two dimensional images: methodology, analysis and classification. In: Dumitrache I, Magda Florea A, Pop F (Eds.), Proceedings of 19th International Conference on Control Systems and Computer Science, Vol. 2: Interdisciplinary approaches in fractal analysis IAFA 2013. The Institute of Electrical and Electronics Engineers, Los Alamitos, CA, USA: 306–312.
- Ristanovic, D, Milosevic NT, Stefanovic BD, Maric DL, Rajkovic K (2010) Morphology and classification of large neurons in the adult human dentate nucleus: a qualitative and quantitative analysis of 2D images. Neurosci Res 67:1–7. [Crossref]
- Miloševic NT, Ristanovic D, Rajkovic K (2012) Mathematical model of box-counting analysis in the human dentate nucleus during development. In: Waliszewski P (Eds.), Fractals and Complexity. Cracow, Poland: 40.
- Dimri GP, Lee X, Basile G, Acosta M, Scott G, et al. (1995) A biomarker that identifies senescent human cells in culture and in aging skin in vivo. Proc Natl Acad Sci U S A 92: 9363-9367. [Crossref]
- Filippi-Chiela EC, Oliveira MM, Jurkovski B, Callegari-Jacques SM, da Silva VD, et al. (2012) Nuclear morphometric analysis (NMA): Screening of Senescence, apoptosis and nuclear irregularities. PLoS ONE 7: e42522. [Crossref]
- Ohshima S (2008) Abnormal mitosis in hypertetraploid cells causes aberrant nuclear morphology in association with H2O2-induced premature senescence. Cytometry A 73: 808–815. [Crossref]
- Stankovic M, Pantic I, De Luka SR, Puskas N, Zaletel I, et al. (2016) Quantification of structural changes in acute inflammation by fractal dimension, angular second moment and correlation. J Microsc 261: 277-284. [Crossref]
- Narita M, Narita M, Krizhanovsky V, Nuñez S, Chicas A, et al. (2006) A novel role for high-mobility group a proteins in cellular senescence and heterochromatin formation. Cell 126: 503-514. [Crossref]
- Gruenbaum Y, Margalit A, Goldman RD, Shumaker DK, Wilson KL (2005) The nuclear lamina comes of age. Nat Rev Mol Cell Biol 6: 21-31. [Crossref]
- Freund A1, Laberge RM, Demaria M, Campisi J (2012) Lamin B1 loss is a senescence-associated biomarker. Mol Biol Cell 23: 2066-2075. [Crossref]
- Ivanov A, Pawlikowski J, Manoharan I, van Tuyn J, Nelson DM, et al. (2013) Lysosome-mediated processing of chromatin in senescence. J Cell Biol 202: 129-143. [Crossref]
- Pantic I, Pantic S, Paunovic J. (2012) Aging increases nuclear chromatin entropy of erythroid precursor cells in mice spleen hematopoietic tissue. Microsc Microanal 18: 1054–1059. [Crossref]
- Testa, G, Gamba P, Di Scipio F, Sprio AE, Salamone P, et al. (2012) Potentiation of amyloid-ß peptide neurotoxicity in human dental-pulp neuron-like cells by the membrane lipid peroxidation product 4-hydroxynonenal. Free Radic Biol Med 53: 1708–1717. [Crossref]
- Choi S, Cho TJ, Kwon SK, Lee G, Cho J (2013) Chondrogenesis of periodontal ligament stem cells by transforming growth factor-ß3 and bone morphogenetic protein-6 in a normal healthy impacted third molar. Int J Oral Sci 5: 7–13.
- Patil R, Kumar BM, Lee WJ, Jeon RH, Jang SJ, et al. (2014) Multilineage potential and proteomic profiling of human dental stem cells derived from a single donor. Exp Cell Res 320: 92-107. [Crossref]
- Pantic I, Harhaji-Trajkovic L, Pantovic A, Milosevic NT, Trajkovic V (2012) Changes in fractal dimension and lacunarity as early markers of UV-induced apoptosis. J Theor Biol 303: 87-92. [Crossref]


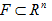 are respectively defined by
are respectively defined by