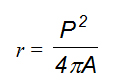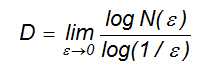Take a look at the Recent articles

Abstract

Breast cancer is the most common malignancy among women, and although advances have been made in our understanding of its molecular and cell behaviour, it remains the second leading cause of cancer death. The need to find a new way of assessing the variability of human “anatomical forms” and their dynamical changes prompted us to discuss the helpfulness of Fractal Geometry as a means of investigating the non-Euclidean morphology of benign and malignant breast mammography lesions. This computer-aided quantitative approach may help to clarify concepts, indicate alternative experiments, and further categorise existing knowledge.

Key words

breast, cancer, mammography, fractals, geometry, image analysis

Introduction

Despite years of intensive study that has been made in understanding women’s susceptibility to breast cancer, it remains a major cause of death worldwide [1,2].

Recent advances in the fields of cell and molecular biology have greatly accelerated research aimed at preventing and treating breast cancer, but a primary element involved in its diagnosis remains radiologists’ ability to interpret the information offered by a mammogram precisely [3-6]. Mammography is a widely diffuse and relatively inexpensive investigative approach, but the consequence of inadequate readings can be dramatic. Several factors may affect the subjective “interpretation” of a mammogram, including the subtle nature of radiographic findings, poor image quality, eye fatigue, and even simply oversight. Overcoming these problems requires not only technically advanced screening methods [7,8], but also answers to the still open question of what makes an “expert radiologist”. At a basic level, the practice of radiology involves looking at an image (i.e. visual perception) and interpreting what is seen (i.e. cognition), and experience gives a radiologist the perceptual and cognitive skills to know what information to look for and how to interpret that information on the basis of the accumulated information processed from previous encounters with similar images. But what makes the task extremely difficult is the fact that, although the “breast anatomy” is essentially the same from one image to another, there is a high degree of variability in both normal [9] and pathological morphology [10], and radiologists can never see all of the possible variations no matter how long they practice or how many images they see. The need to find a new way of observing and quantifying human anatomical forms and their dynamical changes prompted us to discuss the helpfulness of Fractal Geometry for investigating benign and malignant breast mammography lesions.

The non-euclidean geometry of breast lesions

All tumours are classified as benign or malignant. The cells making up a benign tumour are characterised by an “expansive” growth pattern, show no tendency to invade the surrounding environment and never colonise other organs in the form of distant metastases. On the contrary, the absolute criterion of malignancy is “invasiveness”, which means that malignant tumours have an “infiltrative” growth pattern (i.e. malignant cells grow irregularly in the surrounding tissue) and, in many instances, the malignant cells can metastasise some distance from the primary growth.

The continuous generation of “unstable” irregular shapes throughout the progression of breast cancer has led us to define “breast lesions” as prototypic natural fractals [11]. Fractals are mainly characterised by: a) their irregular shape; b) their functional and morphological self-similarity; c) their fractional non-integer dimension; and d) scaling, which means that their measured properties depend on the scale or resolution at which they are measured [12,13].

The most important hallmark of natural fractals is their statistical self-similarity i.e. the small pieces making up natural objects are “kind of like” the whole [13]. Whereas mathematical fractals are invariant over an unlimited range of scales, natural entities are statistically self-similar only within a fractal domain (i.e. “fractal window”) with upper and lower scaling limits, which must be experimentally established [14,15].

Dimension is a geometrical attribute that is mainly defined in two ways. The “topological” or “Euclidean dimension” assigns an integer to every point or set of points in Euclidean space (ε): dimension 0 to a point, dimension 1 to a straight line, dimension 2 to a plane surface, and dimension 3 to a three-dimensional space. The second definition of dimension, or “Hausdorff-Besicovitch dimension” assigns a real number to every natural object in E, lying between the topological dimension 1 and 3.

In 1975, Benoit Mandelbrot (1924-2010), best known as the “father of Fractal Geometry” introduced the symbol Dγ  to indicate the topological dimension and the symbol D to indicate the Hausdorff-Besicovitch dimension [12]. Dγ and D coincide in the case of all of the Euclidean figures, whereas D is >Dγ in the case of fractal objects.

On the basis of the above, two indices have been abstracted for investigating the irregular shape of benign and malignant mammography breast lesions:

1. The index of roundness (r), which can be obtained using the formula,

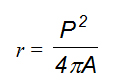
where P is the length of the outer contour of the lesion, A its surface extension, and π the constant pi = 3.14. The coefficient of roundness of circular objects is 1, whereas that of irregular shapes is r >1. The coefficient of roundness indicates a magnitude of the extent to which a breast lesion can be described in terms of a “regular rounded object” (Figure 1). In biological terms, it defines the “degree of expansiveness” of the lesion during the process of growth.

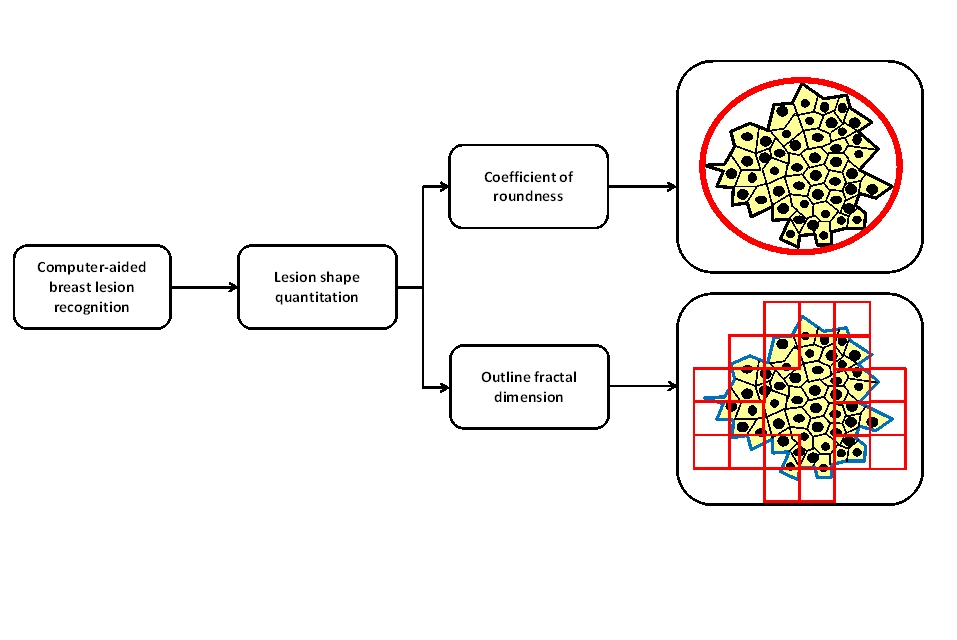
Figure 1. Benign and malignant breast mammography lesions as computable morphological entities. Fractal Geometry may be a helpful tool for studying the irregular shapes of these lesions and their complex growth processes.

1. The fractal dimension of the outer contour of a breast lesion. It can be obtained using the box-counting method [13], which applies the formula

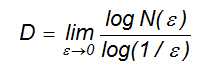
where D is the box counting fractal dimension of the object, ε is the side length of the box, and N(ε) is the smallest number of boxes of side ε required to cover the outer contour of the lesion completely. As the zero limit cannot be applied to biological objects, their dimension is estimated using the formula

D = d                                                                        (3)

where d is the slope of the graph of log {N(ε)} against log (1/ε).

The dimension of the outer contour of a breast lesion provides an estimate of the space-filling properties of the tumour-environment interface (Figure 1). In biological terms, fractal dimension estimates the irregular spatial increase in cell proliferation and their invasion of the surrounding tissue.

The complex growth process of breast cancer

In mathematical terms, breast carcinogenesis can be depicted as a non-linear process that advances in time through qualitatively different states and a number of transitions from one state to another over a certain time interval.

Although breast carcinogenesis is a continuum, pre-malignant states have been identified whose sequence has been used to describe tumour progression [16,17].

The continuous generation of unstable states during its progression has led us to introduce the following definitions:

1. The fractal kinetics of breast cancer, which investigates the temporal fractal changes of a breast lesion without considering the causes determining the changes.
2. The fractal dynamics of breast cancer, which investigates the temporal fractal changes of a breast lesion in relation to the causes determining the changes.

It has been proposed that cancer invasion may be described as a morphological instability that occurs during solid tumour growth [18], and that volumetric growth of a solid cancer depend on the surface extension [19]. This instability may be driven by any “physical” or “chemical” condition, provided that the average cohesion among neoplastic cells decreases and/or their adhesion to the stroma increases [18,20,21]. Anatomical systems exhibiting rough interfaces in their development process can be described by means of scaling analysis [22]. As a result of the fractal nature of the tumour-environment interface, the invasive front possesses a series of both spatial and temporal invariance, which provides the basis for scaling analysis [23]. All these invariance exhibit power law behaviour, and for each type of invariance a critical exponent can be defined as the power law exponent. The power law behaviour arises from the dependence of the interface roughness on the spatial and temporal scales.

On the basis of the above, breast carcinogenesis can be geometrically described using the power-law,

where P and A are the outer contour perimeter and the surface extension of two-dimensional breast mammography lesions, respectively. In this approach, it can be assumed that sequential states of breast lesions growth are characterized by the same dimension D and constant b, i.e. they are statistically self-similar.

Conclusions

According to the Scottish biologist and mathematician D’Arcy W. Thompson (1860-1948), “it is in terms of greatness and direction that we have to report every conception of our forms. The form of an object is defined in fact when we know its greatness, absolute or relative, in the different directions" [24].

Shape is one of the most important features of every anatomical system, as it greatly influences its behaviour and its relationships with the surrounding environment [25].

One of the main issues when evaluating complex living forms and their changes is how to express them quantitatively. Although several numerical indices based on the Euclidean concepts have been introduced in the quantitative analysis of anatomical shapes, they remain extremely approximate because the “rigidity” of linear measures for describing natural objects whose main qualitative attribute is their irregular or fragmented shape.

We are also used to thinking that anatomical entities have a certain shape that is determined by a characteristic scale. If an object is magnified beyond this scale, no new features are revealed and, in order to measure its properties, we do so at a resolution that is finer than its characteristic scale. However, Mandelbrot brought to the attention the fact that natural entities simply do not have this preconceived form, and human beings have structures in space that cannot be characterised by a single spatial scale.

The novelty of fractals lies in their infinite morphological complexity, which contrasts with the harmony and simplicity of Euclidean forms but matches the variety and wealth of complex natural forms.

In conclusion, we can resume that:

1. In accordance with its geometry, benign and malignant mammography lesions can be indexed by fractal parameters.
2. Studying the fractal dynamics of breast cancer may reveal intrinsic and extrinsic factors that influence its rough morphology and its complex growth process.
3. Applying even more sophisticate computer-aided algorithms may reduce the interpretative uncertainty underlying the radiologist’s subjective judgement. Additionally, modelling the growth and development of tumours with specialized algorithms, by combining mathematical tools to the biologic data is a burgeoning area of cancer research [26].
4. Describing breast lesions on the basis of Fractal Geometry may provide new theoretical foundations for the development of new experimental models that can be used in the fight against cancer.

It should be underlined that the above mathematical framework defines benign and malignant breast mammography lesions as computable morphological entities (Figure 1). This way of observing and quantifying benign and malignant breast mammography lesions may help to clarify concepts, interpret new and old experimental data, indicate alternative experiments, and further categorise existing knowledge.

2021 Copyright OAT. All rights reserv

Authorship

The Author designed, drafted the article and revises it critically for important intellectual content. The Author approved the final version of the manuscript.

Conflict of interests

The author declares he has no direct or indirect financial interest connected to the products or information presented in the following paper.

References

1. Jemal A, Siegel R, Ward E, Murray T, Xu J, et al. (2007) Cancer statistics, 2007. CA Cancer J Clin 57: 43-66. [Crossref]
2. Vargo-Gogola T, Rosen JM (2007) Modelling breast cancer: one size does not fit all. Nat Rev Cancer 7: 659-672. [Crossref]
3. Duijm LE, Groenewoud JH, Fracheboud J, de Koning HJ (2007) Additional double reading of screening mammograms by radiologic technologists: impact on screening performance parameters. J Natl Cancer Inst 99: 1162-1170.[Crossref]
4. Kundel HL, Nodine CF, Conant EF, Weinstein SP (2007) Holistic component of image perception in mammogram interpretation: gaze-tracking study. Radiology 242: 396-402. [Crossref]
5. Warren R, Eleti A (2006) Overdiagnosis and overtreatment of breast cancer: is overdiagnosis an issue for radiologists? Breast Cancer Res 8: 205. [Crossref]
6. Moss SM, Blanks RG, Bennett RL (2005) Is radiologists' volume of mammography reading related to accuracy? A critical review of the literature. Clin Radiol 60: 623-626. [Crossref]
7. Law J (2006) The development of mammography. Phys Med Biol 51: R155-167. [Crossref]
8. Miglioretti DL, Smith-Bindman R, Abraham L, Brenner RJ, Carney PA, et al. (2007) Radiologist characteristics associated with interpretive performance of diagnostic mammography. J Natl Cancer Inst 99: 1854-63. [Crossref]
9. Stines J, Tristant H (2005) The normal breast and its variations in mammography. Eur J Radiol 54: 26-36. [Crossref]
10. Kettritz U (2005) Radiological features of breast cancer. Verh Dtsch Ges Pathol 89: 48-51. [Crossref]
11. Grizzi F, Muzzio PC, Di Maggio A, Dioguardi N (2001) Geometrical analysis of benign and malignant breast lesions. Radiol Med 101: 432-435. [Crossref]
12. Gustafson DI, Carr KH, Green TR, Gustin C, Jones RL, et al. (2004) Fractal-based scaling and scale-invariant dispersion of peak concentrations of crop protection chemicals in rivers. Environ Sci Technol 38: 2995-3003. [Crossref]
13. Bassingthwaighte JB, Liebovitch LS, West BJ. Fractal Physiology. Oxford University Press: New York, 1994.
14. Paumgartner D, Losa G, Weibel ER (1981) Resolution effect on the stereological estimation of surface and volume and its interpretation in terms of fractal dimensions. J Microsc 121: 51-63. [Crossref]
15. Losa GA, Nonnenmacher TF (1996) Self-similarity and fractal irregularity in pathologic tissues. Mod Pathol 9: 174-182. [Crossref]
16. Arpino G, Laucirica R, Elledge RM (2005) Premalignant and in situ breast disease: biology and clinical implications. Ann Intern Med 143: 446-457. [Crossref]
17. Perou CM, Sørlie T, Eisen MB, van de Rijn M, Jeffrey SS, et al. (2000) Molecular portraits of human breast tumours. Nature 406: 747-752. [Crossref]
18. Guiot C, Delsanto PP, Deisboeck TS (2007) Morphological instability and cancer invasion: a 'splashing water drop' analogy. Theor Biol Med Model 4: 4. [Crossref]
19. Deisboeck TS, Guiot C, Delsanto PP, Pugno N (2006) Does cancer growth depend on surface extension? Med Hypotheses 67: 1338-1341. [Crossref]
20. Christofori G (2006) New signals from the invasive front. Nature 441: 444-450. [Crossref]
21. Cristini V, Frieboes HB, Gatenby R, Caserta S, Ferrari M, et al. (2005) Morphologic instability and cancer invasion. Clin Cancer Res 11: 6772-6779. [Crossref]
22. Barabasi AL, Stanley HE (1995) Fractal Concepts in Surface Growth. Cambridge University Press: Cambridge.
23. Brú A, Albertos S, Luis Subiza J, García-Asenjo JL, Brú I (2003) The universal dynamics of tumor growth. Biophys J 85: 2948-2961. [Crossref]
24. D’Arcy W. Thompson (1961) On growth and form. Cambridge University Press.
25. Grizzi F, Chiriva-Internati M (2005) The complexity of anatomical systems. Theor Biol Med Model 2: 26. [Crossref]
26. Norton L (2005) Conceptual and practical implications of breast tissue geometry: toward a more effective, less toxic therapy. Oncologist 10: 370-381. [Crossref]