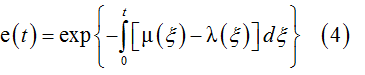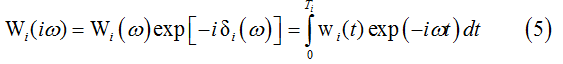The paper presents the development of a new biophysical and computational basis for understanding the non-linear mechanisms of the electrocardiogram (ECG) generation. The ECG is a global scale mass potential which arises from coordinated electrical activity of cardiomyocytes. The multiplicity of cellular processes with extremely intricate mixtures of deterministic and random factors prevents the creation of consistent biophysical models linking global scale ECG with underlying sources of electricity. Consequently, significant aspects of the chaotic dynamics and fractal properties of the heart electrical activity may be hidden in the time course of the ECG components. To test this proposition, we undertake here a radical departure from deterministic equations of classical physics to the probabilistic reasoning of quantum mechanics. A Crucial step consists in the relocation of elementary bioelectric sources from the cellular to molecular level. The corresponding particle model is formulated in terms of a nonhomogeneous birth-and-death process (BDP). Using empirical characteristic functions, we found the global scale solution in the form of a limit distribution function composed from two Gaussian components. This finding discloses the two particle populations associated with the source and sink of the dipole producing the ECG component waveform. On the global scale the corresponding system is described by the system of non-linear differential equations. At the microscopic scale the particle movements are governed by probabilistic laws which we reduce to the rules that define the birth and death rates under the resting and transient conditions. Computer simulations revealed that transition from the resting to transient conditions is characterized by appearance of the deterministic chaos. We term this kind of behavior the “transient deterministic chaos”. Statistical regularities producing the transient deterministic chaos remain invariant for different cellular ensembles. This fractal property supports the statement of statistical self-similarity of ECG constituents.
fractal ECG, transient deterministic chaos, self-similarity, particle model, birth and death process, similar basis function algorithm
The ECG is one of the most efficacious tools in cardiology the diagnostic power of which is supported by remarkable correspondence of various patterns of ECG component waveforms with different normal and pathological conditions of the heart. Diagnostic criteria depend on measurements of timings and amplitudes of component waveforms. A critical limitation of these procedures is that reduction of an ECG signal to its samples at isolated time points is unable to characterize the waveform dynamics. Meanwhile a great deal of experimental evidence indicates that more detailed morphological waveform analysis may expand understanding of the ECG, making this already useful measure even more informative in scientific and clinical settings.
Among the wide variety of quantitative approaches to this problem the nonlinear dynamics, fractals and chaos received considerable attention as potential tools to bridge the randomness and determinism in the mechanisms of ECG generation [1].
Due to apparently irregular character of heartbeat rhythms, heart rate variability (HRV) became a major empirical measure for investigating the chaotic nature of the heart’s electrical activity. Various methods of nonlinear dynamical analysis including the evaluation of fractal scaling exponents, correlation dimensions, power spectra, Lyapunov exponents and detrended fluctuation analysis have been employed to investigate dynamic trends of erratic time series of HRV. Reviews of major results indicate that the variations of inter-beat intervals exhibit a number of characteristic features of deterministic chaos [2,3].
This study exploits the fact that ECG components are global scale mass potential produced by collective behavior of closely located cardiomyocytes. Since millions of cells participate in these processes, it is widely accepted that the dynamics of ECG waveforms reflects summary effects of processes taking place at the microscopic scale. Thus, we may expect that significant aspects of chaotic dynamics and fractal properties of the heart electrical activity are hidden in the time course of the ECG components.
Our goal is to uncover and reconstruct major dynamic and stochastic regularities of cellular processes hidden in the time course of ECG waveforms. Using probabilistic formalism of quantum mechanics we introduce a particle model of ECG generation which bridges global scale ECG components with underlying elementary sources of electricity. Identification of the model parameters on empirical grounds provides means to reconstruct in computer simulations microscopic events underlying ECG generation.
ECG resembles electrical phenomena occurring in ensembles of multiple cardiomyocytes immersed in an interstitial fluid. Elementary bioelectric sources acting at the microscopic scale are ions, both positively and negatively charged particles, which cross the cell membrane in both directions. The cell membranes have high resistance, compared with the resistance of the extracellular space [4]. Thus, the membranes serve as a separating material that divides the muscle tissue into extracellular and intracellular compartments. Because little current from extracellular sources flows through the cell membrane the dipoles associated with the ECG constituents are produced by specific ensembles of extracellular ions.
After release from the cell, extracellular ions have a possibility to cross the membrane in the opposite direction, i.e., to return to the interior of the cell. Balanced ion transport lacks significant power to produce measurable changes in potential differences between various spatial locations in the external media. An event that disturbs this balance and has potential to produce a waveform deflection at the global scale is a transient synchronization of ion flows across cellular membranes of large ensembles of closely located cardiomyocytes. Such complex events occur in a sequential order during the cardiac cycle and may be associated with different ECG components.
Given the multiplicity of molecular mechanisms underlying ECG generation, we need to avoid detailed description of the internal processes acting on the microscopic scale. For a solution we refer to the formalism of quantum mechanics addressed to a wide variety of systems in nature that can be regarded as many-particle ensembles with extremely intricate dynamics of their elements [5]. Such systems are typically formed of huge ensembles of particles, with essentially erratic motion, so a description of the individual elements is really hopeless. However, this is not necessary in practical terms because only cumulative effects are expressed in the global scale variables. At this level, details of the individual particle motions are averaged – only the mean characteristics are essential for a description of the global scale dynamics. This is a cornerstone of the indeterminacy principle in quantum mechanics [5].
A classic example is Brownian motion which portrays the macroscopic picture emerging from randomly moving particles [6]. On the microscopic level, at any time step, the particle receives a random displacement, caused by other particles hitting it or by an external force. Different models of particle collective behavior have been developed for various physical applications in such fields as gases, fluids, superfluids, electrons and ions in conductors, semiconductors, plasma, nuclear matter in neutron stars, etc [7].
For the problem in question, we need to describe the temporal evolution of the size of the external particle population related to the transport processes between the extracellular and intracellular particle compartments. We address this problem using the theoretical framework of previous modelling studies of the short-term synaptic plasticity in which the “birth-and-death” process (BDP) has been settled as a tool for analysis of transmembrane particle transfers [8,9]. The membrane is considered as a boundary that separates the internal and external particle compartments. We regard crossing the membrane by an ion as an elementary event interpreted as the birth or death of a particle producing a unit increase or decrease of the population size.
Since particle movements are governed by probabilistic rules, we measure the size of relevant extracellular particle population at time t by integer-valued random variable X(t) (boldface letters denote random variables). From a variety of BDP models we choose the nonhomogeneous BDP in which the birth and death rates λ(t) and μ(t) may be any specified functions of the time t [10].
Since inter-state transitions are governed by probabilistic laws, the future of BDP is not uniquely determined. A major condition is that during a sufficiently small element of time, Δ, the probability of the change of the X(t) by more than one particle is negligibly small:
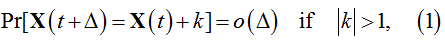
where Pr denotes probability and k is an integer.
Therefore, the particle system changes only through transitions from states to their nearest neighbours. An increase of the population size by a unit represents the birth, 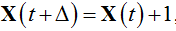 , whereas a decrease by a unit represents the death,
, whereas a decrease by a unit represents the death, 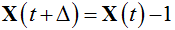 . The probabilities of these events for nonhomogeneous BDP are [11]:
. The probabilities of these events for nonhomogeneous BDP are [11]:
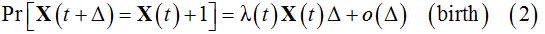
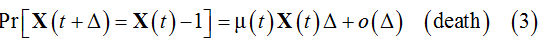
where λ(t) and (μt)are the birth and death rates, respectively.
The expected population size related to these microscopic events is defined by the integral equation [11]
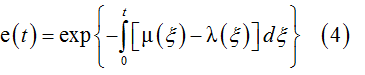
This is an average of X(t) variables measured in different trials, i.e. the limiting behavior of a large number of random events. In this probabilistic context we regard e(t) as a distribution function.
The frequency domain counterpart of distribution function is the characteristic function defined by the Fourier transform [12]. Retaining all the information possessed by distribution function, characteristic function has been appreciated as an effective tool for numerical manipulations with empirical data [13]. The method of empirical characteristic function developed on this conceptual basis is widely favored in the time series analysis of stationary processes [14].
A new feature we add to the method is that the signal in question, i.e., the ECG, is a non-stationary process produced by a number of sources. We use the method of fragmentary decomposition as theoretical and computational tool which provides means to decompose a non-stationary bioelectric signal into the set of functionally meaningful components [15]. We regard such component as an empirical distribution function produced by nonhomogeneous BDPs and defined by equation (4).
Non-stationary ECG v(t) submitted to the fragmentary decomposition is conditioned to form the time series  , where vm=v(tm), tm=mΔ, m is an integer, M is the number of samples and Δ is the sampling interval. Fragmentary decomposition starts from the adaptive segmentation procedure. The objective is to estimate segmentation points which define EEG fragments associated with functional components in the form of peaking waveforms. The segmentation points are defined as zero-crossings and points of global and local minimums of the modulus of v(t).
, where vm=v(tm), tm=mΔ, m is an integer, M is the number of samples and Δ is the sampling interval. Fragmentary decomposition starts from the adaptive segmentation procedure. The objective is to estimate segmentation points which define EEG fragments associated with functional components in the form of peaking waveforms. The segmentation points are defined as zero-crossings and points of global and local minimums of the modulus of v(t).
More particularly, if
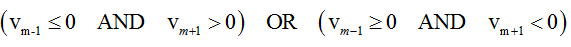
then τi =tm is qualified as zero-crossing (segmentation point), where i is the number of segmentation point.
The point τi =tm (i is the number of segmentation point) specifies a global or local minimum of v if
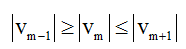
A sequence of segmentation points 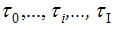 is so formed. Figure 1 shows an example of adaptive segmentation with zero-crossings illustrated in vertical red lines and minimums illustrated in vertical blue lines.
is so formed. Figure 1 shows an example of adaptive segmentation with zero-crossings illustrated in vertical red lines and minimums illustrated in vertical blue lines.
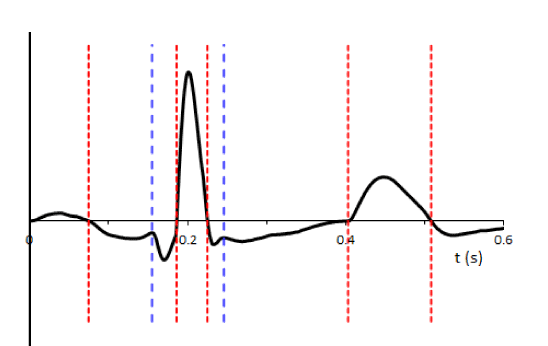
Figure 1. . Illustrates adaptive segmentation of ECG record. Vertical lines indicate segmentation points
Given ECG fragment of the length Ti = τi+1-τi between the segmentation points τi and τi+1 (i=0,…,I-1), we define empirical distribution function as wi(t)=v(t+τi) where t takes values from 0 to Ti. The corresponding empirical characteristic function is defined by the exponential finite Fourier integral
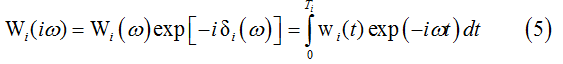
where Wi(ω) is the amplitude spectrum (AS), δi(ω) is the phase function (PF), ω=2πf, f is frequency and i=√-1. Since the treatments of the frequency characteristics are universal, the subscripts are omitted in the following text.
Integrals of the type (5) deal with relatively short ECG segments of different lengths. The most readily available technique of digital spectral analysis using the fast Fourier transform is not suited for short-time spectral analysis. As an adequate tool for numerical calculations of finite Fourier integrals (5) we use the similar basis function algorithm [16], an original version of Filon-type methods that provide maximum precision in the numerical estimation of trigonometric integrals.
The complex spectrum (5) is fully defined by the real valued W(ω) and δ(ω). According to the fragmentary decomposition method the AS of a functionally meaningful component is adequately expressed by Gaussian function.
We examined this proposition using standard 12 lead ECGs of healthy subjects from the two sources. First, records for a group of 14 healthy subjects (7 males and 7 females; age 22-62 years, mean 38.6 years) from the outpatient cardiac clinic of the Macquarie University (Sydney, Australia). Second, records of 7 males and 7 females (age 22-58 years, mean 39.9 years) from the group of healthy subjects in the PTB diagnostic ECG database [17,18].
As empirical characteristic we used to test the “Gaussianity” was the normalized AS 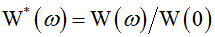 . The fits of analytical Gaussian functions to numerous numerically calculated spectra indicate striking resemblance of empirical W*(ω) with the analytical function
. The fits of analytical Gaussian functions to numerous numerically calculated spectra indicate striking resemblance of empirical W*(ω) with the analytical function
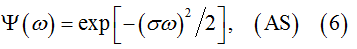
where σ is a parameter.
Typical result is illustrated in Figure 2. The vertical dotted lines in Figure 2a show the ECG fragment chosen for identification. Functionally, it corresponds to the T wave. The blue line in Figure 2b is the normalized AS W*(ω) computed from this fragment. The red line shows the fit of the Gaussian template (6) with σ=25.6 (ms).
Similar results of the spectral analysis applied to the 5 fragments (P, Q, R, S and T waves) of the ECG in Figure 3a are illustrated in Figure 3b.
General form of Ψ(ω) is characteristic for a low pass filter conventional parameter of which is the cut-off frequency FC. At this frequency the attenuation of the AS drops by 3dB, i.e. 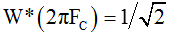 . The arrow in Figure 2b shows such defined frequency Fc=5.25 Hz.
. The arrow in Figure 2b shows such defined frequency Fc=5.25 Hz.
Using FC, we define the AS normalized by both the amplitude and frequency as
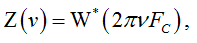
where ν=f/FC is dimensionless normalized frequency.
Given (6) as the model of W*(ω), an expected form of Z(ν) is the Gaussian spectrum defined as

Using G(ν) as a template, Figure 3c exemplifies typical results of sticking together Z(ν) and G(ν) at ν=1 which corresponds to ω=2πFC. The frequency FC estimated from this condition defines 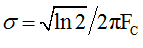 .
.
To test the adequacy of such fits we define FB as the boundary frequency below which the mean square error between Ψ(ω) and W*(ω) does not exceed an empirically established threshold ε=0.0002. Using FB we evaluate dimensionless extension coefficient kE=FB/FC the values of which for ECG components from Figure 3a are presented in the Table 1. For the R waves of ECGs from 14 healthy subjects we found the following kE ranges. (1) Outpatient cardiac clinic: from 1.91 to 3.16 (mean 2.49). (2) PTB database: from 1.82 to 3.63 (mean 2.46).
Similar results documented for different ECG components from various leads and subjects indicate random fluctuations of kE and an erratic character of the spectral components above FB. This allows us to regard W*(ω) as the sum of Ψ(ω) and a random component produced by different artefacts. In this context equation (6) defines expected form of AS.
With regard to the phase components, the tests revealed the condition under which numerically computed phase function δ(ω) shows consistency with a simple linear model
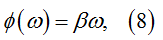
where β is parameter.
We found that if kE >1.5, the numerically computed PF δ(ω) only slightly deviates from linearity over the frequency range from 0 to FC. Typical result is illustrated in Figure 2c where the arrow indicates Fc.
Thus the estimation of β is reduced to the calculation of linear regression lines using δ(ω) samples from the [0, ωC] interval. The slope of the regression line serves as the estimate of β.
Approved analytical dependencies (6) and (8) define the complex spectrum
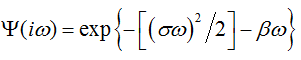
the time domain counterpart of which may be regarded as a generic model of ECG component.
Since we deal with the casual process, either the real or imaginary part of Ψ(iω) is sufficient to find its the time domain counterpart ψ(t), i.e. the time domain model of w(t) [19]. Using the imaginary part, we define the model at t>0 by the sine Fourier transform
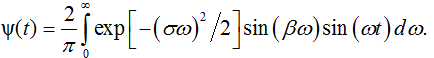
This integral has an analytical solution [20]
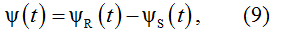
where
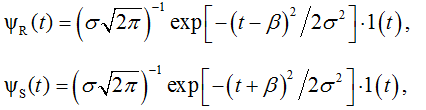
1(t) is a unit step function.
At t>0 equation (9) is consistent with the wave function in a general form of the d'Alembert's solution [21]. In this context, the process described by equation (9) may be regarded as an impulse response of a dynamic system governed by the following system of nonlinear differential equations:
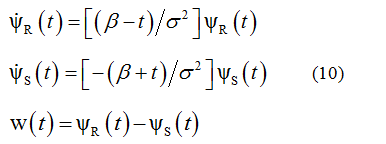
where 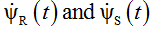 denote the derivatives of
denote the derivatives of 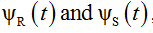 , respectively.
, respectively.
The form of these equations allows us to qualify the system as a non-autonomous system, that is, a system driven by time-varying signals.
Function ψ(t) as well as equations (10) are fully determined by the results of the frequency domain identification of AS and PF which provide the values of the parameters σ and β. Taking an additional parameter κ=W(0), we regard κψ(t) as a voltage between the poles of an extracellular dipole. The red line in Figure 2a illustrates the T component computed on this basis. Using parameter values from the Table 1, the colored lines in Figure 3a illustrate analytical solutions (9) obtained for P, Q, R, S and T components.
Table 1. Parameters of ECG components
|
κ |
Σ |
β |
Fc |
kE |
μV |
Ms |
ms |
Hz |
RU |
P |
4.13 |
21.1 |
52.4 (0.0202) |
6.31 |
2.29 |
Q |
-3.45 |
6.93 |
15.1 (0.039) |
19.1 |
2.09 |
R |
9.73 |
5.02 |
11.4 (0.00111) |
26.3 |
2.09 |
S |
-4.01 |
5.5 |
10.8 (0.0185) |
24 |
2.09 |
T |
5.5 |
24 |
70.1 (0.183) |
15.8 |
2.63 |
Parameters κ, σ, β, FC and kE were identified for each of P, Q, R, S and T ECG components shown in Figure 1a. Values of kE are in relative units (RU).
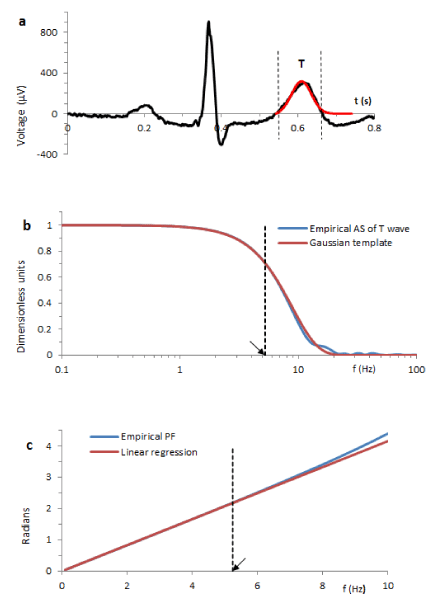
Figure 2. The vertical dotted lines indicate ECG segment (T wave) submitted to the spectral analysis. b. The blue line is AS of the T wave computed by the similar basis function algorithm. The red line is Gaussian template with σ=25.6 (ms). The curves of empirical AS and template are stuck together at FC=5.25 Hz. This frequency is indicated by the arrow. c. Comparison of the PF (blue line) with linear regression line computed over the frequency range from 0 to FC. The arrow shows this frequency on the natural frequency scale.
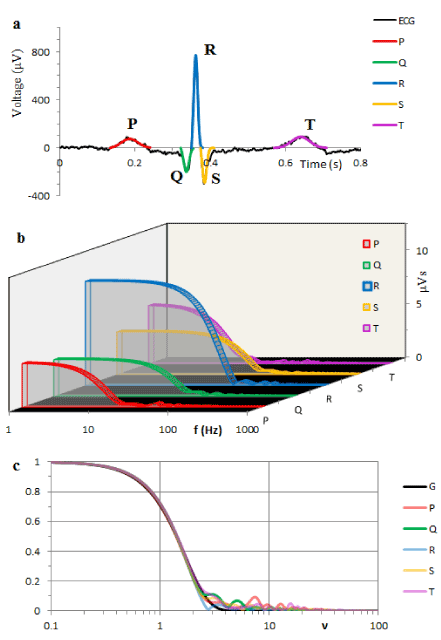
Figure 3. The black line illustrates typical human ECG recorded from the lead II. Conventional components represent succession of P, Q, R, S and T waves. Colored lines are model components drawn according to equation (9) with the parameters κ, σ and β from Table 1. b. Shows the ASs of P, Q, R, S and T waves from Figure 1a. c. Colored lines are the ASs from b after normalization of both the amplitude and frequency. The black line shows the Gaussian function (7).
With regard to the component composition of equation (9), we consider ψR(t) and ψS(t) as the source and sink elements of the dipole associated with the underlying particle populations “R” (Resource) and “S” (Sink), respectively.
The next question to consider is how elementary sources acting at the microscopic level produce global scale transients (9). To specify the birth and death rates in terms of σ and β parameters, we refer to equations (1)-(3). We regard the reference point t=0 as the time instant from which the BDP transfers from the resting conditions governed by the constant birth and death rates λR, μR, λS and μS to the transient conditions governed by the time dependent birth and death rates λR(t), μR(t), λS(t) and μS(t).
To describe transient behavior of the population R we replace λ(ξ) and μ(ξ) by specified functions λR(ξ) and μR(ξ), respectively. Accordingly, e(t)=ψR(t). Using unique solution of equation (4) for these conditions, we deduce the following rules that govern the transient behavior of the sub-population R:
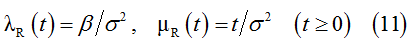
To apply similar deductions to the population S, we replace λ(ξ), μ(ξ) and e(t) by λS(ξ), μS(ξ) and ψS(t), respectively. The corresponding solution of equation (4) provides the following rules that govern the transient behavior of sub-population S:
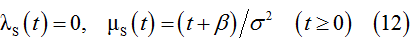
Constant birth and death rates for resting conditions are derived by exclusion the time t from (11) and (12). Thus, the rules for the resting conditions are as follows.
Sub-population R:
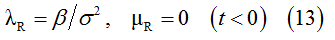
Sub-population S:
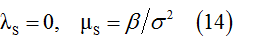
Disclosure of these probabilistic rules provides means to move from the global scale descriptions of the particle populations in terms of characteristic functions to numerical simulations of particle populations at the microscopic scale.
The number of particles X(t) in particular trial is computed step by step for consecutive points 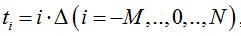 , where Δ is a small element of time. The corresponding time series is presented by the discrete samples
, where Δ is a small element of time. The corresponding time series is presented by the discrete samples 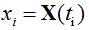 . The time point t0 is taken as an instant at which the resting conditions are switched to the transient conditions.
. The time point t0 is taken as an instant at which the resting conditions are switched to the transient conditions.
The choice of Δ is made in compliance with condition (1) which states that during a sufficiently small element of time Δ, the probability of a change in the population size by more than one element is negligibly small. Consequently, permitted size of the particle population at the time ti+1 is: xi+1=xi+1 (birth), xi+1=xi (unchanged size) or xi+1=xi-1 (death).
The probabilities of such inter-state transfers are expressed by equations (2) and (3) which we rewrite in the following form:
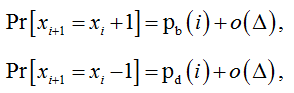
where pb(i) and pd(i) are the probabilities of a particle birth and death, respectively, in the time interval from ti to ti+1.
2021 Copyright OAT. All rights reserv
Under the resting conditions which persist until ti<t0, the R and S particle sub-populations behave as simple BDPs with the birth and death rates defined by equations (13)- (14) .
Thus we obtain the following probabilities of the birth and death of a particle in 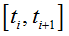 interval (i=-M,..,-1):
interval (i=-M,..,-1):
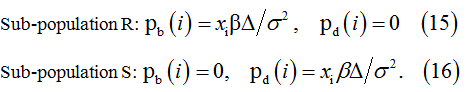
Under the transient conditions induced at the time instant t0 the particle populations develop as non-homogenous BPDs with the birth and death rates defined by equations (11)-(12). The corresponding probabilities of the birth and death in 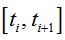 interval
interval
(i=0,…,N-1) are:
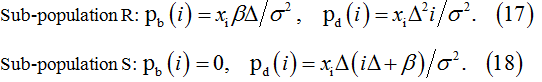
We organized the calculations as the succession of standard steps dealing with the time intervals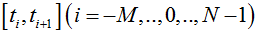 . Given the step beginning from ti, the xi serves as the initial condition. The value xi+1 which X(t) takes at the end of the interval is computed using Monte Carlo simulations.
. Given the step beginning from ti, the xi serves as the initial condition. The value xi+1 which X(t) takes at the end of the interval is computed using Monte Carlo simulations.
The procedure for each step is as follows:
- Estimate probabilities pb(i) and pd(i) using equations (15)-(16) for the steady-state conditions and equations (17)-(18) for the transient conditions.
- Pick out random real numbers
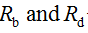 using a random number generator to produce real numbers in the range from 0 to 1.
using a random number generator to produce real numbers in the range from 0 to 1.
- Estimate the size of the particle population at the end of the interval:
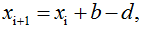
where b and d are binary numbers defined as follows:
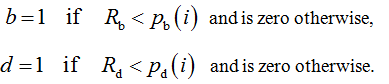
Numerical experiments have been supported by a specially designed computer program written by the first author in the object Pascal language of Embarcadero Delphi 2010.
Using the algorithmic framework for Monte Carlo simulations, our goal was the reconstruction of the microscale origins of the global scale equation (9). Thus, we deal with temporal developments of particle numbers XR(t) and XS (t) in different trials. The number of particles producing a dipole is defined as XD(t)= XR(t)- XS (t).
To perform simulations, it was important to choose the value of Δ under which the probabilities pb(i) and pd(i) are low enough to be consistent with the condition (1). Based on a number of numerical experiments with different parameters, the value Δ=0.0001 ms was selected for numerical simulations illustrated in figures 4 and 5. The segmentation points were ti=i∙Δ with i taking values from -2∙105 to 3∙105. The corresponding time interval extended from -20 to 30 ms with t=0 corresponding to the switch from the resting to transient conditions. The values of the parameters σ and β were taken from the Table 1 for the component R. Thus, σ=5.02 ms and β=11.4 ms.
As an initial condition, an equal size N0=20 was prescribed to both sub-populations. The particle population sizes in Figure 4a and Figure 5 are expressed in relative units, i.e.
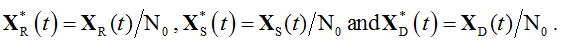 .
.
Typical single trial trajectories of the sub-population sizes are illustrated in Figure 4a for the source and sink. The underlying probabilities of the birth and death events are shown in Figures 4b and 4c.
At t<0 the development of particle populations is governed by constant birth and death rates defined by formulas (13)-(14). Thus, we deal with simple BDP. Accordingly, for each sub-population the probabilities of the birth and death are identical in the time interval from -20 ms to 0. The differences between different trials have purely statistical origins. This type of behaviour is free from deterministic trends, i.e. we deal with stationary stochastic processes.
The transition from the resting to transient condition was simulated as the change of the constant rates of the birth and death to the time dependent rates (11)-(12). The change occurs in a “smooth” fashion. This means that the sizes of the particle sub-populations developed under the resting conditions serve as initial conditions for the transient regimes.
At t>0 the probability of the birth in the sink sub-population is zero. Thus, as seen from Figure 4a, the transient conditions lead to a relatively fast flow of particles from external compartment to internal compartment.
In contrast, the size of the source sub-population is governed by the complex interplay of the birth and death probabilities. Onset of the transient conditions gives rise to both probabilities. Initially, the birth probability prevails over the death probability. During this process the size of the source sub-population increases and reaches the maximum at approximately t=12.8 ms. The succeeding developments show dominance of the death probabilities. As the result, the size of the source sub-population declines and returns to the resting conditions. Thus, under the transient conditions an erratic particle behavior is strongly influenced by deterministic trends. We deal with deterministic chaos.
The population sizes of the source and sink from Figure 4a are redrawn and separately shown in Figure 5a (blue line) and Figure 5b (red line). The black line in Figure 5c is the sum of these populations. The mixture of stochastic and deterministic components of these processes at t>0 is a characteristic feature of deterministic chaos.
In order to compare consistency of computed single trial trajectories with the global scale deterministic solutions (9) we need to estimate the limiting behavior of the particle populations. A useful approach to disclose the expected trajectories is averaging. The dotted lines in Figure 5 show the averages of 5 single trial processes. Obviously, these procedures reduce variability and bring simulation results to a better proximity with expected trends.
To support precise comparisons we need to set up equal numbers of particles in both the source and sink populations at the time t=0 from which the transients evolve. To realize this condition we start simulations from t=0.
The blue lines in figures 6 a, b and c exemplify 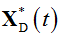 in single trials computed for particle population with 10, 50 and 100 particles. The red lines in Figure 5 show the averages of 5 single trial realizations from each particle population. Comparison of these statistical averages with the black lines (function ψ(t) with corresponding parameters) shows that increase of the particle numbers makes single trial samples indistinguishable from the theoretical solution. This is convincing evidence of the deterministic chaos hidden in the time course of the global scale ECG. Due to a temporary appearance of this effect, we name the uncovered mixture of deterministic and stochastic processes the “transient deterministic chaos”.
in single trials computed for particle population with 10, 50 and 100 particles. The red lines in Figure 5 show the averages of 5 single trial realizations from each particle population. Comparison of these statistical averages with the black lines (function ψ(t) with corresponding parameters) shows that increase of the particle numbers makes single trial samples indistinguishable from the theoretical solution. This is convincing evidence of the deterministic chaos hidden in the time course of the global scale ECG. Due to a temporary appearance of this effect, we name the uncovered mixture of deterministic and stochastic processes the “transient deterministic chaos”.
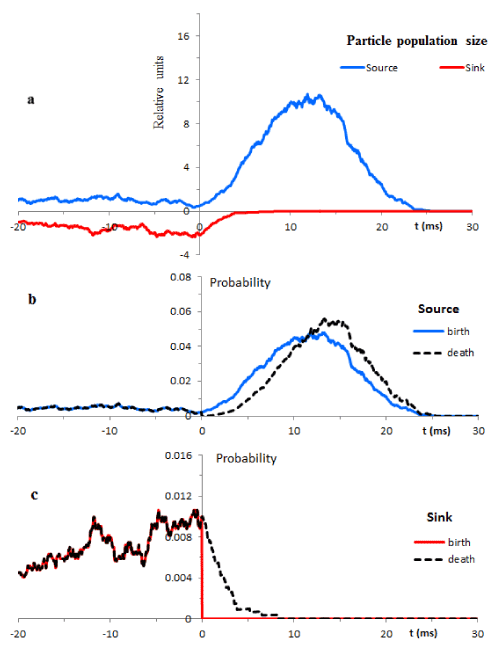
Figure 4. Illustrates temporal evolution of the source and sink particle populations in typical trials. Resting conditions computed from -20ms are switched at t=0 to the transient conditions. b, c. Illustrate the birth and death probabilities drawn according to equations (15) – (18).
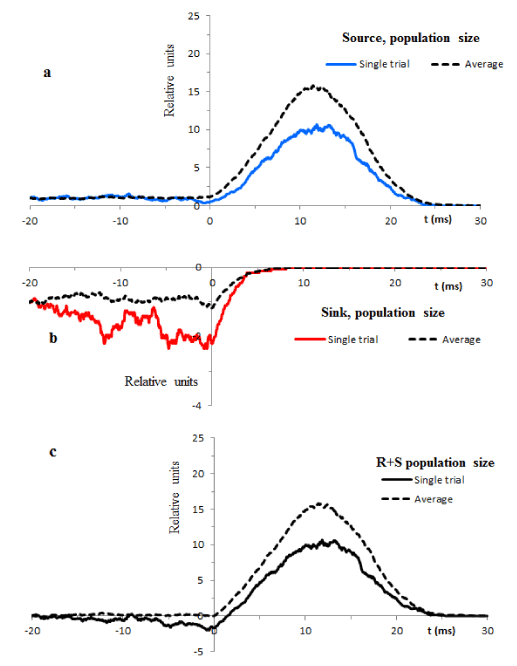
Figure 5. Solid lines illustrate typical changes of population sizes in single trials. The dotted lines are the averages of 5 arbitrary selected single trial records.
The Mandelbrot concept of a fractal is most often associated with objects satisfying criterion of self-similarity which means that an object is composed of similar sub-units that resemble the structure of the whole object [22]. The theory and numerical simulations presented in this paper provide evidence of common statistical and deterministic rules that govern generation of ECG functional components from different ensembles of multiple cardiomyocytes. For example, Figure 6 illustrates similar global scale effects produced by particle populations containing different numbers of particles. This means that cellular ensembles may be divided into the constituent parts governed by the same probabilistic and deterministic rules as the whole ensemble. We summarize this outcome as the following statement of the statistical self-similarity of ECG constituents.
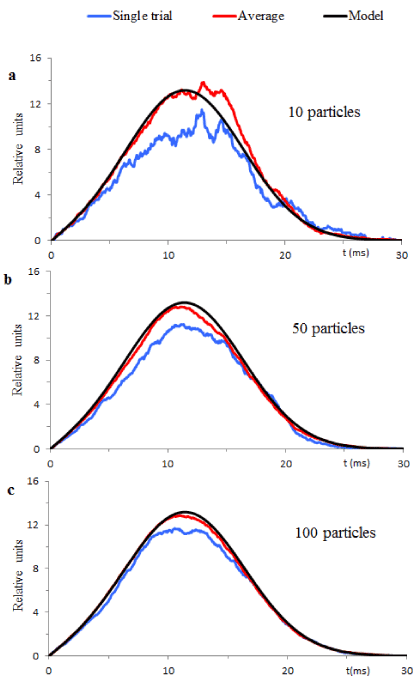
Figure 6. Compares theoretical solutions with the results of computer simulations of the particle models. The black lines show theoretical solutions drawn according to equation (9) with parameters σ and β from Table 1 for the R component. Blue lines exemplify 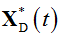 computed for different particle populations. The red lines are the averages of 5 single trials.
computed for different particle populations. The red lines are the averages of 5 single trials.
Statistical self-similarity statement: Consider function ψ(t) with σ and β parameters as the model of ECG component generated by synchronous activation of a large ensemble L of closely located cardiomyocytes. Let us extract a part of L regarded as an ensemble S. We state that the global scale effect produced by the S is fully expressed by the changes in the values of σ and β parameters while the form of analytical function ψ(t) remains invariant.
This statement differs drastically from conventional deterministic treatments which regard membrane potentials as “building blocks” the linear summation of which produces a global scale ECG [23]. Suppose that the membrane potential is described by a certain function with M parameters. Linear summation of the effects produced by J cells must take into account the parameters of J functions and contain JM free parameters. Given that millions of cells participate in the ECG generation, this is a highly under-determined task. Actually, the large number of details and free parameters delivered to the linear summation can often obscure rather than illuminate the essentials of the underlying events.
In contrast, a compact set of σ, β and κ parameters accumulates all essential aspects of the underlying events at the microscopic scale without changes to the general form of analytical ψ(t). This constitutes the basis for consideration the samples of the transient deterministic chaos as fractal objects
The results of the identification the ECG components from various leads in different subjects can be summarized by stating that the time domain counterpart (9) of empirical frequency domain AS (6) and PF (8) can be regarded as a universal formula for a monolithic ECG waveform. The corresponding source is described by the system of non-linear equations (10).
Probabilistic interpretations of equation (9) in terms of the distribution function provided means to identify the two interrelated particle population as the sources of an extracellular dipole producing the ECG component waveform. Using non-homogenous BDP as a theoretical framework, the rules (11)-(14) governing the birth and death rates were deduced.
This probabilistic basis of our approach provided means to reduce an intractably huge number of the measures of heart electrical activity to a universal model of ECG component with the fewest parameters (σ, β and κ). Being limit distributions for the sums of random variables, these parameters discriminate those aspects of the molecular machinery that are significant on the global scale from those that are not.
The removal of irrelevant variables is a crucial outcome of our radical departure from the superposition principle which interprets the ECG as a linear superposition of membrane potentials. Conceptually, we relocate the elementary sources of electricity from the cellular to the molecular level. At this microscopic scale of bioelectric activities we deal with particle movements governed by the defined rules of the birth and death processes. The vanishingly small role of individual particles in the generation of global scale processes reduces the problem to the study of the limiting behavior of large numbers of independent random variables [24].
The most important probability distribution in this context is the normal (Gaussian) distribution because, in accordance with the central limit theorem, any process of random sampling tends to produce a normal distribution of sample values, even if the whole population from which the samples are drawn does not have a normal distribution. Single normal distribution is not suitable to account of the temporal changes in the system from which the samples come. We regard empirically grounded appearance of two symmetric Gaussian functions in our model (9) as a solution which overcomes this limitation. It is difficult to escape the conclusion that ψ(t) may be regarded as a time dependent statistical distribution applicable to wide classes of physiological processes.
Computer simulations provided means to investigate the role of deterministic and stochastic factors involved into the ECG generation. An important finding is the difference between the resting and transient conditions. Under the resting conditions the particle movements across membranes are balanced and lack power to produce measurable changes of ECG waveforms. Mass potentials produced by these particle movements belong to the category of stationary stochastic processes.
The component generation is triggered by some external signal. On the global scale this event is reflected by transient potentials the dynamics of which is perfectly described by equation (9). Phenomenologically, the global scale potential is generated by collective behavior of a large ensemble of cardiomyocytes. Using computer simulations we reconstructed transient potentials produced by small fragments of the large ensemble. The point that we do consider to be established is that potentials developing during transient conditions contain deterministic component and thus represent the mixture of stochastic and deterministic processes characteristic for the deterministic chaos. However the deterministic components are vanishingly small during the resting conditions. To take into account the changing statistical character of mass potentials we have introduced the notion of the transient deterministic chaos.
Remarkable fractal property of the transient deterministic chaos follows from the invariance of the limiting statistical distribution (9) applied to different particle ensembles. Thus, a wide range of monolithic deflections identified in the time course of human ECG may be qualified as fractal entities related by the statistical self-similarity.
The principles presented here can be readily extended to many other types of biomedical signals, specifically electroencephalograms, and work in this direction is in progress.
D.M. and E.B. formulated the major approach. D.M. developed mathematical and computational tools. E.B. obtained ECG records using which both authors provided empirical support of the methods. Both authors wrote the paper.
- Goldberger AL (1990) Nonlinear dynamics, fractals and chaos: Applications to cardiac electrophysiology. Ann Biomed Eng 18: 195-198. [Crossref]
- Mansier P, Clairambault J, Charlotte N, Médigue C, Vermeiren C, et al. (1996) Linear and non-linear analyses of heart rate variability: a minireview. Cardiovasc Res 31: 371-379. [Crossref]
- Xinbao N, Chunhua B, Jun W, Ying C (2006) Research progress in nonlinear analysis of heart electric activities. Chinese Science Bulletin 51: 385-393.
- Geselowitz DM (1989) On the theory of the electrocardiogram. Proceedings of the IEEE 77: 857-876.
- d’Espagnat B (1999) Conceptual Foundations of Quantum Mechanics (Perseus Books, Reading, Massachusetts, 1999).
- Marters P, Peres Y (2010) Brownian Motion. (Cambridge University Press, Cambridge 2010).
- Mahnke R, Kaupuzs J, Lubashevsky I (2009) Physics of Stochastic processes. (WILEY-VCH Verlag GmbH&Co. KGaA, Weinheim, 2009).
- Melkonian D (1990) Mathematical theory of chemical synaptic transmission. Biological Cybernetics 62: 539-548.
- Melkonian DS (1991) Double barrier quantal model of neurotransmitter release. Neuroreport 2: 719-722. [Crossref]
- Bharucha-Reid AT (1960) Elements of the Theory of Markov Processes and their Applications. (McGraw- Hill, New York, 1960).
- Kendall DG (1948) On the generalized “birth-and-death” process. Ann Math Statist 19: 1-15.
- Lukacs E (1970) Characteristic functions. (Griffin, London, 1970).
- Parzen E (1962) On estimation of a probability density function and mode. Ann Math Statist 33: 1065–1076.
- Feuerverger A, Mureika RA (1977) The empirical characteristic function and its applications. The Annals of Statistics 5: 88-97.
- Melkonian D, Blumenthal TD, Meares R (2003) High resolution fragmentary decomposition – a model based method of non-stationary electrophysiological signal analysis. J Neurosci Methods 131: 149-159. [Crossref]
- Melkonian D (2010) Similar basis function algorithm for numerical estimation of Fourier integrals. Numerical algorithms 54: 73-100.
- Bousseljot R, Kreiseler D, Schnabel A (1995) Nutzung der EKG-Signaldatenbank CARDIODAT der PTB über das Internet. Biomedizinische Technik 40: 317 (1995).
- Goldberger AL, Amaral LA, Glass L, Hausdorff JM, Ivanov PC et al. (2000) PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 101: 215-220.
- Papoulis A (1962) The Fourier Integral and its Applications (McGraw-Hill, NewYork, 1962).
- Erdelyi A (1954) (Ed). Tables of Integral Transforms, Vol. 1 (McGraw-Hill, New York, 1954).
- Bekefi G, Barrett AH (1987) Electromagnetic Vibrations, Waves, and Radiation. (MIT Press, Cambridge, 1987).
- Mandelbrot BB (1982) The Fractal Geometry of Nature (Freeman and Company, New York, 1982).
- Gulrajani RM1 (1998) The forward and inverse problems of electrocardiography. IEEE Eng Med Biol Mag 17: 84-101, 122. [Crossref]
- Gnedenko BV, Kolmogorov AN (1968) Limit distributions for sums of independent random variables (Addison-Wesley Publishing Company, Massachusetts, 1968).