The lack of a unified definition of reliability function in system design phase may contribute to the difficulty in improving the reliability of nanotechnology drug delivery systems. The reliability function is frequently used in reliability engineering and gives the probability of an item operating for a certain amount of time without failure. As such, the reliability function is a function of time. In this paper we define the notion of reliability function in the context of drug targeting in cancer treatment. This function gives the probability of all cancerous cells being destroyed in a certain amount of time. Having defined our notion of the reliability function, we propose a model for this function based on Ito type stochastic differential equations. We also describe an algorithm for computing the minimum dose level to achieve a desired value for expected time needed to destroy all cancerous cells.
ito concepts, gaussian process, stochastic differential equations, nanoconjugate
| C |
the number of nanoconjugates that are carrying the drug and they are injected into the blood stream
|
| S (t) |
the number of nanoconjugates that are still at the site of administration at time t |
| S1 (t) |
the number of nanoconjugates that are in non-targeted tissues at time t |
| I1 (t) |
the number of nanoconjugates that are in cancerous cells population at time t |
| I2(t) |
the number of nanoconjugates that are in healthy cells population at time t |
| R (t) |
the number of nanoconjugates that are eliminated at time t |
| d1 |
the average number of nanoconjugates that penetrate cancerous cells population
in the targeted tissue per unit time
|
| d2 |
the average number of nanoconjugates that penetrate healthy cells population
in the targeted tissue per unit time
|
| d3 |
the average number of nanoconjugates that penetrate the non-targeted tissues per unit time |
| d4 |
the average number of nanoconjugates that are eliminated from non-targeted
tissues per unit time
|
| d* |
=(d1+d2+d3 ) |
| γ1 |
the average number of nanoconjugates that are eliminated from cancerous cells population
in the targeted tissue per unit time
|
| γ2 |
the average number of nanoconjugates that are eliminated from healthy cells population
in the targeted tissue per unit time
|
| λ |
the average number of cancerous cells that are killed per unit time |
| λ1 |
the average number of cancerous cells population is expanded per unit time |
| d1* |
the average number of cancerous cells being eliminated per unit time= λ-λ_1 |
| k |
Number of nanocojugates, carrying the drug, needed to destroy
a cancerous cell in the tissue
|
| N(t) |
the number of cancerous cells in the tissue at time t |
| n |
the number of cancerous cells in the tissue at time 0 |
| T |
the first time all cancerous cells will be destroyed |
| P(t) |
the reliability of a nanodrug delivery system = P(T≤ t) |
| E(T) |
expected time required to kill all cancerous cells |
| Bj (t) |
standard Brownian motion, j=1,2,3,4,5 |
| σj (t) |
diffusion coefficient, j=1,2,3,4,5. |
The focus of the nanotechnology therapeutic approaches to treat cancer has been on early disease detection, drug discovery and monitoring, controlled release of therapeutic agents, and targeted drug delivery. See Mansoori [1] for more details. Targeted drug delivery requires statistical modeling to establish the reliability in success of drug targeting. Unreliable nanotechnology drug delivery systems are a major source of user frustration. We believe that the key to make more reliable systems is first understand what makes a nanotechnology drug delivery system unreliable [2] defined the instantaneous (or point) reliability of a nanotechnolgy drug delivery system for cancer therapy as the probability of killing all cancerous cells at the single instant in time. Instantaneous reliability is typically used in the military, as it is sometimes necessary to assess the reliability of a system at a specific time of interest. However, we are often interested in the reliability of a nanotechnology drug delivery system over a period of time. Throughout this paper we refer to it as the reliability function. In this paper we first introduce the notion of the reliability function of a nanothechnology drug delivery system for cancer therapy. Our notion of reliability function is a generalization of Ebrahimi and Mansoori [2] definition and varies over time. We then report on our efforts to determine an optimal dose of the drug to achieve a desired average time required to kill all cancerous cells for a cancer nanotechnology drug delivery system. It should be mentioned that the question of how to assess reliability for nanotechnology based engineering systems was recently studied by some researchers. For more details about this line of research see Ebrahimi [3-5] and many references cited there.
The paper is organized as follows. In Section 2, we present a time dependent stochastic differential equation for modeling the number of nanoconjugates that penetrate cancerous cells population in the tissue. In section 3, we introduce notion of reliability function and propose a model for this function. In this section, we also give an algorithm to compute an optimum dose level to achieve a desired value for expected time needed to kill all cancerous cells. Two examples are provided in this section to illustrate our proposed methodology. Concluding remarks are provided in Section 4.
Let us consider a nanoconjugate containing the drug which has potential either to attach to the surface of a cancerous cell or to go inside a cancerous cell in a targeted tissue. Suppose C is the number of these nanoconjugates that are injected into the blood stream. Since our interest is only on cancerous cells, for simplicity of our presentation, we assume that the targeted tissue is made of two groups. Group one consists of all cancerous cells and group two consists of all noncancerous cells. Throughout this paper we refer to a noncancerous cell as a healthy cell. Now, as the time proceeds, each nanoconjugate can be in one of the five possible states; still at the site of administration, penetrated non-targeted tissues, penetrated group one, penetrated group two, or removed from the body. Let S (t) and S1 (t) be the number of nanoconjugates that are still at the site of administration and in non-targeted tissues at time t, respectively. Also, let l1 (t) and l2 (t) be the number of nanoconjugates that are in groups one and and two at time t, respectively. Finally, let R(t) be the number of nanoconjugates that are already eliminated from the body at time t. Note that Ii(0)=S1(0)=R(0)=0,i=1,2 and S(0)=C (Figure 1) summarizes the process of elimination of nanoconjugates.
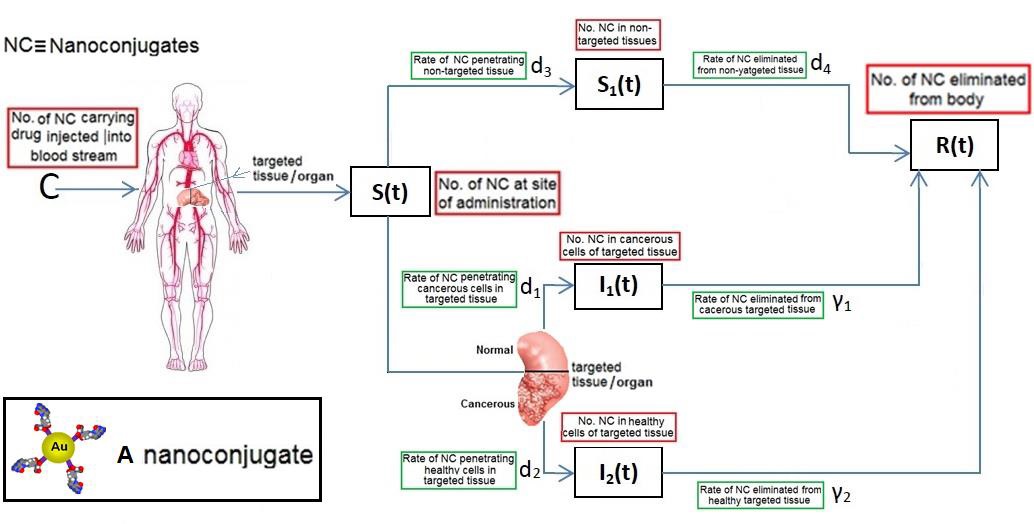
Figure 1.Process of elimination of nanoconjugates
It is known that most drugs used in clinical practice will show first order rate elimination processes, see Jambheker and Breen (2012) [6]. For a nanodrug delivery system this means that the number of nanoconjugates will decrease at a rate that is proportional to S(t). Using this fact, from Figure 1, we can describe the elimination of nanoconjugates from the body through the following four ordinary differential equations:
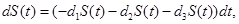 (1)
(1)
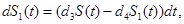 (2)
(2)
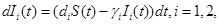 (3)
(3)
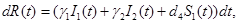 (4)
(4)
where γi is the rate of elimination of nanoconjugates from the group i, i=1,2, di is the rate that nanoconjugates penetrate the group i, i=1,2, d3 is the rate that nanoconjugates penetrate non-targeted tissues, and d4 is the rate of elimination of nanoconjugates from non-targeted tissues. Since major aim of most nanocarrier applications has been to deliverthe drug to tumor site, meanwhile avoiding drug delivery to normal sites as much as possible to reduce adverse effects, we expect that d1 and d2 to be much larger than d3 and also d1 to be larger than d2 Solving the equation (1) and using the fact that S(0)=C we get
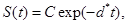 (5)
(5)
where d*=d1+d2+d3 see Tenenbaum and Pollard (1985) [7]. Also, solving the resulting differential equations give
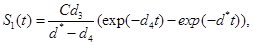 (6)
(6)
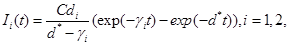 (7)
(7)
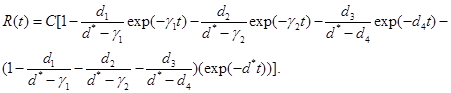 (8)
(8)
From the equation (8) it is clear that as t approaches to infinity, the R(t) approaches to C. Also, since R(t) must be a non-decreasing function in t, we need γ1, γ2 and d4 to be less than or equal to d*.
Typically, stochastic differential equations incorporate random white noise which is the derivative of a standard Brownian motion. Since it is a basic clinical observation that variability always exists within a group of patients, we introduce stochastic perturbation terms into the equations (1)-(3). Having done that the resulting stochastic differential equations are:
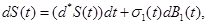 (9)
(9)
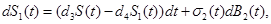 (10)
(10)
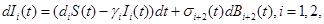 (11)
(11)
where σj(t),j=1,2,3,4 are known as intensity fluctuation functions, and Bj(t),j=1,2,3,4 are independent Standard Brownian Motions. Note that in our situation we do not need to model R(t), because R(t)+S(t)+S1+I1(t)+I2(t)=C In general, the process B(t) is said to be Standard Brownian Motion if P(B(0)=0)=1 , B (t) has stationary independent increments, and B (t) has Normal distribution with mean zero and variance t. For more details about this process see Ross (1996) [8].
Now, one can show that the solutions to (9)-(11) are
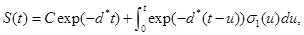 (12)
(12)
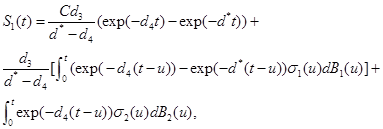 (13)
(13)
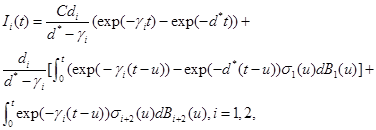 (14)
(14)
respectively, see Oksendal [9].
The following lemma gives several properties of Gaussian processes
S(t),S1(t)and Ii(t),i=1,2
Lemma 1.Below are properties of Gaussian processes S(t),S1(t) and S(t),S1(t)
(a) 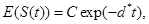 ,
,  and
and 
(b) Suppose  and
and  .That is,
.That is, 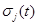 goes to zero as t approaches infinity. Then,
goes to zero as t approaches infinity. Then, 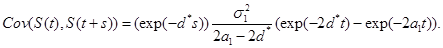 .
.
(c) Under the model in part (b), 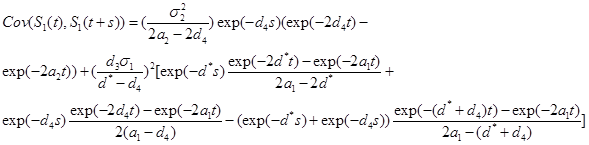
(d) Under the model in part (b) 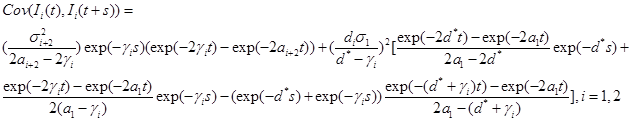
Let N(t) be the number of cancerous cells still in the targeted tissue at time t. Define,
2021 Copyright OAT. All rights reserv
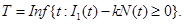 (15)
(15)
In equation (15), T represents the first time that all cancerous cells will be destroyed and a targeted tissue will be cancer free. Now, we define
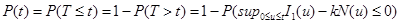 (16)
(16)
We refer to P (t) as the reliability function of nanotechnology drug delivery systems for cancer therapy.
From (16), P(t) gives the probability of a targeted tissue be cancer free before time t. A higher P(t) suggests the system is more reliable. Also, expected value of T, E(T), gives average time required to kill all cancerous cells. It should be noted that k, the number of nanoconjugates needed to kill a cancerous cell, depends on the size of a cancerous cell and can be determined in an Vivo experiment. Usually, if the size of a nanoconjugate is much smaller (or larger) than the size of a cancerous cell, then one needs to deliver hundreds of (or few) nanoconjugates to kill a cancerous cell. See for example Zharov et al., Mansoori et al., Keyhanian et al., Hashemian et al., and Letfullin and George [10-14].
It is worth mentioning that the classical definition of reliability function is defined in-terms of the survival distribution function of its lifetime. For more details about the classical notion of reliability see Lawless [15].
Now to calculate P(t) we need to model N(t). Following arguments similar to the ones used in sections (2.1) and (2.2), we use the following stochastic differential equation,
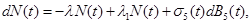 (17)
(17)
where λ is the rate cancerous cells are killed , λ1 is the rate cancerous cells proliferate and B5 (t) is a Standard Brownian Motion.
Given N(0)=n solving the equation (17) gives
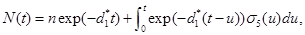 (18)
(18)
Where d1*=λ-λ1 From the equation (18), it is clear that EN (t)=n(d1* t) and
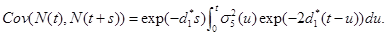 (19)
(19)
Under the model, 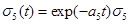 the equation (19) reduces to
the equation (19) reduces to
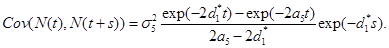 (20)
(20)
Corollary 1.Under the model ,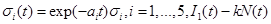 is a Gaussian process with mean
is a Gaussian process with mean
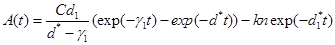 (21)
(21)
and covariance function,
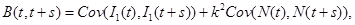 (22)
(22)
where 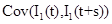 is given by part(d) of Lemma 1 and
is given by part(d) of Lemma 1 and 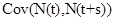 is given by the equation (20).
is given by the equation (20).
Proof. Use Lemma 1, part(a) and Ito concepts, which says that for any deterministic function g, the process 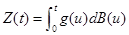 is Gaussian process with mean zero and
is Gaussian process with mean zero and
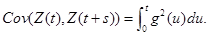 See Freedman (1975) [17] Ω
See Freedman (1975) [17] Ω
Now to compute we need the probability density function of T. The following theorem gives its probability density function.
Theorem 1. Under the assumtions of Corollary 1, the probability density function of T, is approximately given by
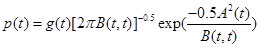 (23)
(23)
where
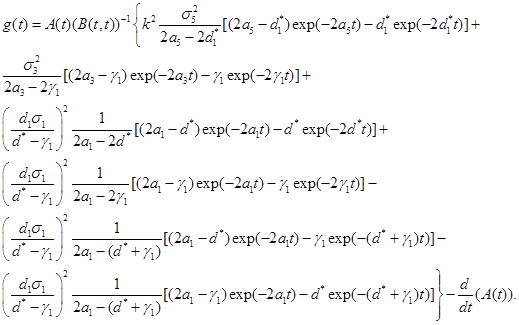
Proof. Use the equation (5) from Durbin (1985) [16] and equations (20)-(22). Ω
From the equation (23), it is clear that’s E(t) a decreasing function in C.
Unfortunately, Nanotechnology reliability is a new field and data are not publicly available to apply to our proposed model. Thus, in the following example we illustrate our method by assigning numbers to all the parameters in the model.
Example 1. Suppose we have designed a nanotechnology drug delivery system with C=420 n=100 a1 =a3=a5=0.1 σ1=σ3=σ5=1 ,d1=0.8,d2=0.1,d3=0.1 . Also, assume that the size of a nanocojugate is much larger than a cancerous cell and we only need K=3 to kill the cancerous cell. For this system, B(t,t)=8.5exp(-.2t)-7.5exp(-1.4t)-12.1exp(-1.6t)+20exp(-1.8t)-8.9exp(-2t) ,A(t)=1680exp(-.8t)-1680exp(-t)-300exp(-0.7t) ,and g(t)=A(t)(B(t,t))-1[-4.2exp(-.2t)+5.2exp(-1.4t)+9.7exp(-1.6t)-18exp(-1.8t)+8.3exp(-2t)]-(1680exp(-t)+1344exp(-.8t)-210exp(-.7t)). Using the equation(23), the reliability function is given by, 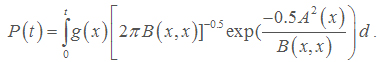 . Figure 2, gives the reliability function as a function of t. One can also compute
. Figure 2, gives the reliability function as a function of t. One can also compute 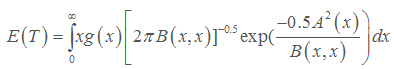 which is about 1.1. That is, for this nanotechnology drug delivery system it will take in average about 1.1 time units to kill all cancerous cells. From Figure 2, it is also clear that the chance of killing all cancerous cells within 2 time units is almost 100% (Figure 2).
which is about 1.1. That is, for this nanotechnology drug delivery system it will take in average about 1.1 time units to kill all cancerous cells. From Figure 2, it is also clear that the chance of killing all cancerous cells within 2 time units is almost 100% (Figure 2).
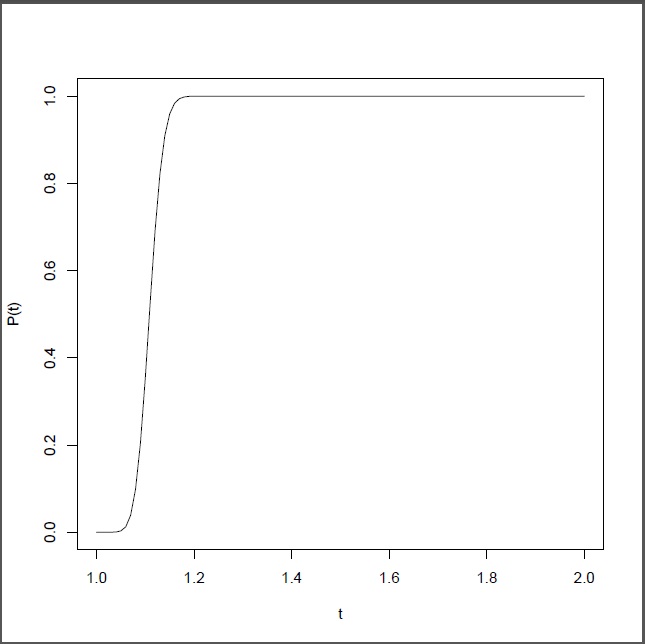
Figure 2.Reliability function of the nanotechnology drug delivery system for cancer therapy
Our proposed criteria to find an optimal C is: Find the lowest C such that the average E (T) takes some desired value, say α. That is we want the lowest dose such that T= α. Now to obtain our optimal C that achieves α mean, we propose the following algorithm. It should to be noted that our algorithm is similar to gradient method. However, here the domain of our function is all positive integers [18,19].
Algorithm:
- Choose an initial value for C say C=C0 then compute E (T) If this average is bigger than α, take C=C0+1 and compute the expected value again. Continue this until for the first time E(T) is less than or equal to α. Our recommendation is that as initial value take C0=nk.
- If for C0 the E (T) less than α. Then, take C=C0 -1 and computed the expected value again. Continue this until for the first time E (T) is larger than or equal to α. Suppose C* is the answer. Now, if for C=C8 , E (T) is exactly α, then the optimal solution is C* . If it is larger than α, then the optimal solution is C=C^* +1
It is worth mentioning that since E(T) is a decreasing function in C, our algorithm gives the global minimum. The following example illustrates application of our Algorithm. Again in this example we assign numbers to some of the parameters in our model.
Example 2. Suppose a1=a3=a5=0.1, σ1=σ3=σ5=1, d1=0.8,d2=0.1,d3=0.1,γ1=0.8, λ=0.8 and λ1=0.1. Our goal is to design a nanotechnology drug delivery system that achieves a certain value for E(T). Table 1, gives the minimum number of nanoconjugates that should be injected into the blood stream for different values of E(T), n, and k. For example, if n=100,E(T)=2,and k=3, then we need to inject 400 nanoconjugates into blood stream (Table 1).
Table 1: Minimum number of nanoconjugates
| n=100, k=3, E(T)=2 |
C=400 |
| n=1000, k=3, E(T)=2 |
C=6289 |
| n=1000, k=1, E(T)=2 |
C=1680 |
| n=1000, k=3, E(T)=2.5 |
C=5682 |
| n=100, k=3, E(T)=2.5 |
C=385 |
| n=1000, k=1, E(T)=2.5 |
C=1598 |
Remark: One can also use the following criteria to find optimal C: Find the lowest C needed to destroy all cancerous cells within certain time with some level of certainty , say probability ≥0.95. Algorithm similar to one used for the previous criteria can also be used to obtain optimal C.
In this paper, we have introduced a unified definition of reliability function for nanotechnology drug delivery systems in cancer therapy. Our notion provides a general framework for assessing reliability and it is very flexible and easy to use. As one expects, our finding shows that, one can achieve a specific value for E(T) with low dose level by having small k. By increasing k the dose level increases exponentially. Also, by increasing E(T), the dose level decreases.
The work of the first author is partially supported by the National Science Foundation, DMS1208273.
- Amiji M (2007) Nanotechnology for cancer therapy. CRS Press, Floida
- Ebrahimi N, Mansoori GA (2014) Reliability for Drug targeting in cancer treatment through nanotechnology (A psychometric approach). IntJMed Nano Res1.004.
- Ebrahimi N (2014) Assessing the reliability of a nanocomponent using nanocrack growth. Applied Stochastic Models in Business and Industry 30: 294-302.
- Ebrahimi N, Mccullough K, Xiao Z (2013) Reliability of Sensors Based on nanowire Networks Operating in a Dynamic Environment. IEEE Transactions on Reliability 4: 908-916.
- Ebrahimi N, Mccullough K, Xiao Z (2013) Reliability of sensors based on nanowire networks modeled by equilateral triangle and hexagonal lattices. IEEE Transactions on Nanotechnology 81-95.
- Jambhekar SS, Breen PJ (2012) Basic Pharmacokinetics,secod edition. Pharmaccutical Press, London, UK
- Tenenbaum M, Pollard H (1985) Ordinary differential equations. Dover, New York.
- Ross S (1995) Stochastic Processes. Second edition,Wiley
- Oksendal B (2003) Stochastic differential equations. An introduction with applications. Spriger,Germany
- Zharov VP, Lutfullin RR, Galitovskaya EN (2005) Microbubbles-overlapping mode for laser killing of cancer cells with absorbing nanoparticle clusters. J Phys D: Appl Phys 38: 2571-2581
- Mansoori GA, Brandenburg KS, Shakeri-Zadeh A (2010) A comparative study of two folate-conjugated gold nanoparticles for cancer nanotechnology applications. Cancers (Basel) 2: 1911-1928. [Crossref]
- Keyhanian K, Mansoori GA, Rahimpour M (2010) Prospects for Cancer Nanotechnology Treatment by Azurin. Dynamic Biochemistry, Process Biotechnology and Molecular Biology 4: 48-66.
- Hashemian AR, Mansoori GA (2013) Cancer Nanodiagnostics and Nanotherapeutics through the Folate- Conjugated Nanoparticles. J Bioanal Biomed 5: 061-064.
- Letfullin RR, George TF (2013) Plasmonic nanomaterials in nanomedicine. Handbook of nanomaterials: 1063-1097.
- Lawless JF (2002) Statistical models and methods for lifetime data. Second edition,Wiley.
- Durbin J (1985) The first passage of a continuous Gaussian process to a general boundary. J Appl Probab 22: 99-122.
- Freedman A (1975) Stochastic differential equations and applications. Acad. Press.
- Mansoori GA (2005) Principles of Nanotechnology- Molecular-Based Study of Condensed Matter in Small Systems. World Scientific Pub. Co.
- Mansoori GA , Mohazzabi P, McCormack P, Jabbari S (2007) Nanotechnology in cancer prevention, detection and treatment: bright future lies ahead. World Review of Science, Technology and Sustainable Development (WRSTSD) 4: 226-257.


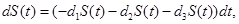 (1)
(1)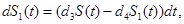 (2)
(2)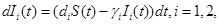 (3)
(3)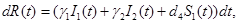 (4)
(4)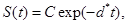 (5)
(5)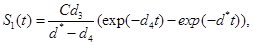 (6)
(6)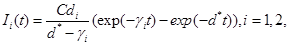 (7)
(7)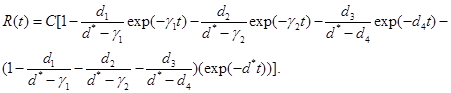 (8)
(8)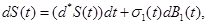 (9)
(9)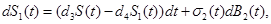 (10)
(10)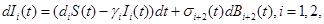 (11)
(11)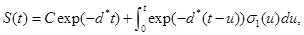 (12)
(12)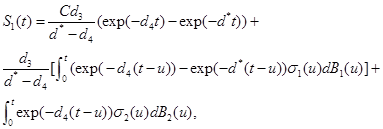 (13)
(13)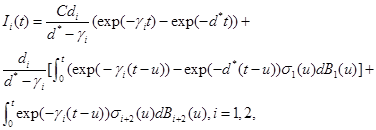 (14)
(14)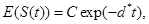 ,
, 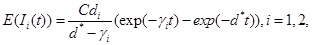 and
and 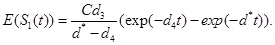
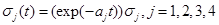 and
and 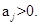 .That is,
.That is, 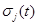 goes to zero as t approaches infinity. Then,
goes to zero as t approaches infinity. Then, 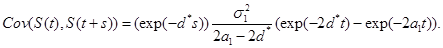 .
.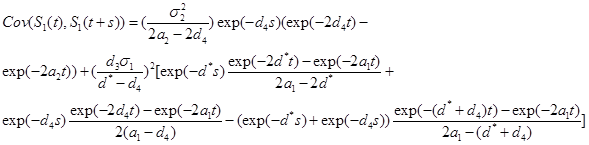
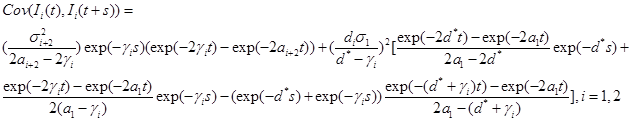
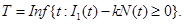 (15)
(15)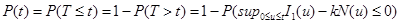 (16)
(16)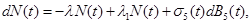 (17)
(17)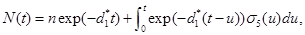 (18)
(18)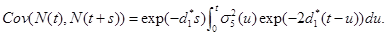 (19)
(19)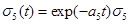 the equation (19) reduces to
the equation (19) reduces to 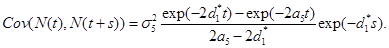 (20)
(20)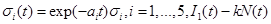 is a Gaussian process with mean
is a Gaussian process with mean 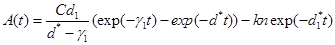 (21)
(21)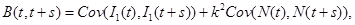 (22)
(22)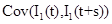 is given by part(d) of Lemma 1 and
is given by part(d) of Lemma 1 and 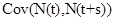 is given by the equation (20).
is given by the equation (20). 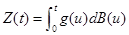 is Gaussian process with mean zero and
is Gaussian process with mean zero and
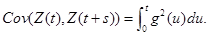 See Freedman (1975) [17] Ω
See Freedman (1975) [17] Ω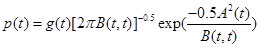 (23)
(23)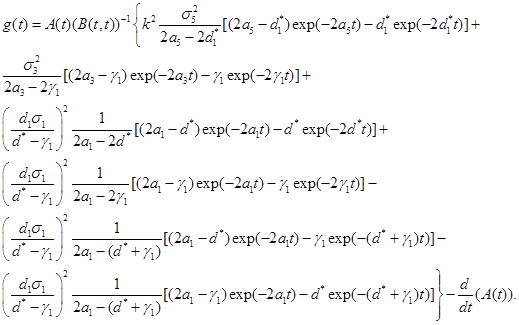
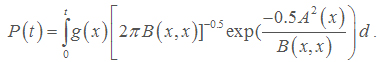 . Figure 2, gives the reliability function as a function of t. One can also compute
. Figure 2, gives the reliability function as a function of t. One can also compute 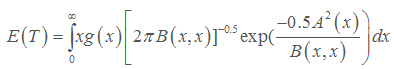 which is about 1.1. That is, for this nanotechnology drug delivery system it will take in average about 1.1 time units to kill all cancerous cells. From Figure 2, it is also clear that the chance of killing all cancerous cells within 2 time units is almost 100% (Figure 2).
which is about 1.1. That is, for this nanotechnology drug delivery system it will take in average about 1.1 time units to kill all cancerous cells. From Figure 2, it is also clear that the chance of killing all cancerous cells within 2 time units is almost 100% (Figure 2).