Abstract
A set having a non-integer Hausdorff-Besicovitch dimension (popularly known as fractal dimension) is called fractal [1-3]. The concept of fractal creates a geometry called fractal geometry where the shapes exhibit self-similarity(strictly speaking, self-affinity) at all scales of magnification or dilution [1-3].
Shapes created by fractal geometry or evaluated by fractal dimension have a great deal of significance in terms nonlinear science and engineering. All basic sciences (biology, physics, and chemistry) and applied sciences (biomedical engineering, manufacturing engineering, and alike) have been benefited by the shape modeling ability of the fractal geometry and shape evaluating ability of the fractal dimension.
However, a random walk consisting of some contracting mappings known as Iterated Function System (IFS) has been developed to create fractals [4]. An IFS-generated fractal (e.g., the fractal shown in the left-hand-side in Figure 1) is nothing but a point-cloud (i.e., a set of randomly generated points). However even though one can model a complex shape using a fractal, it may not be manufactured accurately [5,6]. Therefore, remodeling of fractals is necessary.A possible way, is the one by Sharif Ullah et al. [5,6], that have developed some procedures to remodel an IFS-fractal. A remodeled fractal is shown in the right-hand-side of Figure 1. The main idea is to control the levels of self-similarity by having a deterministic walk replacing the random walk among the contracting mappings. The remodeled fractal shown in Fig. 1 exhibits self-similarly up to the third level.To find out the degree of similarity among the original and remodeled fractal, one can use the DNA based computing [7].
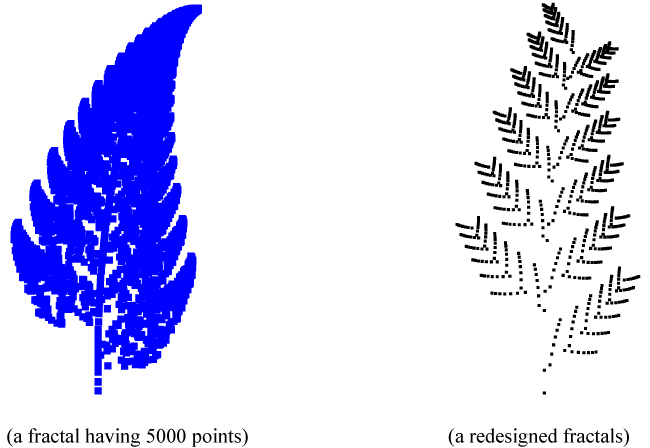
Figure 1. Remodeling of an IFS-generated fractals
References
- 1. Mandelbrot BB(1982)The Fractal Geometry of Nature, W. H. Freeman: San Francisco.
- 2. Stewart DE (2001) Towards numerically estimating Hausdorff dimensions. The ANZIAM Journal 42: 451-461.
- 3. Hutchinson JE (1981) Fractals and self-similarity. Indiana University Mathematics Journal 30: 713-747.
- 4. BarnsleyMF, Demko S (1985) Iterated Function Systems and the Global Construction of Fractals. Proceedings of the Royal Society of London Series A: Mathematical and Physical Sciences 399: 243-275.
- 5. Sharif Ullah AMM, Sato Y, Kubo A, Tamaki J (2015) Design for manufacturing of IFS fractals from the perspective of Barnsley's fern-leaf. Computer-Aided Design and Applications 12: 241-255.
- 6. Sharif Ullah AMM, Omori R, Nagara Y, Kubo A, Tamaki J (2013) Toward Error-free Manufacturing of Fractals. Procedia CIRP 12: 43-48.
- 7. Ullah AM, D'Addona D, Arai N (2014) DNA based computing for understanding complex shapes. Biosystems117: 40-53. [Crossref]
Editorial Information
Editor-in-Chief
2021 Copyright OAT. All rights reserv
Bianciardi Giorgio
University of Siena
Article Type
Editorial
Publication history
Received date: August 05, 2015
Accepted date: August 10, 2015
Published date: August 12, 2015
Copyright
©2015 Ullah AMMS. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Citation
Ullah AMMS (2015) Remodeling Fractals. Fractal Geometry and Nonlinear Anal in Med and Biol 1: doi: 10.15761/FGNAMB.1000107
Corresponding author
AMM Sharif Ullah
Department of Mechanical Engineering, Kitami Institute of Technology, 165 Koen-cho, Kitami, Hokkaido 090-8507, Japan, Tel/Fax: 157-26-9207.
E-mail : ullah@mail.kitami-it.ac.jp

