Digital imaging techniques have enabled to gain insight into complex structure-functional processes involved in the neo-cortex maturation and in brain development, already recognized in anatomical and histological preparations. Despite such a refined technical progress most diagnostic records sound still elusive and unreliable because of use of conventional morphometric approaches based on a unique scale of measure, inadequate for investigating irregular cellular components and structures which shape nervous and brain tissues. Instead, these could be efficiently analyzed by adopting principles and methodologies derived from the Fractal Geometry. Through his masterpiece, The Fractal Geometry of Nature, Benoît Mandelbrot has provided a novel epistemological framework for interpreting the real life and the natural world as they are, preventing whatever approximation or subjective sight. Founded upon a body of well-defined laws and coherent principles, the Fractal Geometry is a powerful tool for recognizing and quantitatively describing a good many kinds of complex shapes, living forms, organized patterns, and morphologic features long range correlated with a broad network of functional interactions and metabolic processes that contribute to building up adaptive responses making life sustainable. Scale free dynamics characterized biological systems which develop through the iteration of single generators on different scales thus preserving proper self-similar traits. In the last decades several studies have contributed to showing how relevant may be the recognition of fractal properties for a better understanding of nervous tissues biology in healthy conditions, in pathological states and in those cases that pertain to forensic criminology.
fractal geometry, fractal dimension, scaling window, resolution power, neurons, brain tissue, forensic neurosciences
The Fractal Geometry of Nature [1], Benoît Mandelbrot’s masterpiece, evokes a new ‘‘Weltanschauung,’’ providing a novel epistemological approach for interpreting the natural world and a more intelligent vision of life itself. The fractal geometry, which was founded on a body of well-defined laws and coherent principles, including those derived from chaos theory, allows the recognition and quantitative description of complex shapes, images, and other figures that usually are created through unlimited iterations of a simple generator (often a mathematical motif) by means of computer-aided design (CAD). CAD figures undecipherable using classical geometry were referred to as ‘‘fractals’’ because of their peculiarity, which lies in the reproducibility of their shape over a range of scales and in a non integer topological dimension called a ‘‘fractal dimension’’, from the Latin word fractus. Non-Euclidean iterated figures – now including fractals – have often been considered to bear a resemblance to pathological entities or mathematical monsters despite of – or owing to – their beauty, richness and fascinating shapes . Nowadays, most of these have become explicable and even familiar, since Mandelbrot’s assertion that they can almost be considered as a general rule of Nature. This led Mandelbrot to conclude that «clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line». Subsequently, it was noted that these virtual figures share some morphological traits and self-similar properties which could be encountered not only in elements of the inanimate world, but also (though less evident) in complex forms, functions and shapes belonging to the plant and animal realms. Living forms develop according to organized morphological patterns correlated with a complex system of functional metabolic interactions which make the accomplishment of the adaptive response possible. Iteration, self-similarity, form invariance upon scaling, nonequilibrium thermodynamics, self-organization, and energy dissipation are among the mechanisms reputed to sustain the emergence and maintenance of living forms, in contrast to those of homeostasis, linearity, smoothness, regularity, and thermodynamic reversibility pertaining to a more traditional vision based upon the concepts and rules of Euclidean geometry and adequate for an ideal world [2]. Over the past decade, a large amount of experimental evidence has been accumulated showing that biological elements do indeed express statistical self-similar patterns and fractal properties within a defined interval of scales. This is termed the ‘‘scaling window,’’ in which a direct relationship between the observation scale and the measured size/length of an object or the frequency of a temporal event can be ascertained and in turn quantified by a peculiar FD [3]. In other words, the FD of a biological component remains constant within the scaling window, and serves to quantify variations in length, area or volume with changes in the dimensions of the measuring scale. However, real ‘‘fractality’’ exists only when the experimental scaling range covers at least two orders of magnitude, although fractality over many orders of magnitude has been observed in various natural fields. Hence, defining a ‘‘scaling range’’ of length measurements appears to be an inescapable requisite for assessing the fractality of any biological element. Experimental evidence of a definite scale interval avoids any ambiguous assignment of objects or figures lacking that requirement, and confirms Mandelbrot’s assertion that «fractals are not a panacea; they are not everywhere» [1].
Most cells, tissues, organs – in either the animal or vegetal realms – are systems in which the component parts and unit fragments assemble with different levels of complexity and organization. This means that a single fragment or element may, on various scales, reproduce the whole object from which it is derived; in other words, it is self-similar, albeit in a statistical sense. Very few of these shapes can be analytically described or evaluated by using Euclidean geometry, which was developed to trace the regular and ideal geometrical forms that are practically unknown in natural and biological systems. Although the first coherent essay on fractal geometry was published in French more than 30 years ago [2,4], it may be worth considering exactly how and when the ‘‘heuristic introduction’’ of such an innovativ discipline occurred or, more pregnantly stated, as when ‘‘the irruption of fractal geometry’’ into the life sciences such as biology and medicine actually took place. Although there is no precise date, it is generally agreed that such introduction occurred within the ‘‘golden age’’ of cell biology – that is, between the 1960s and 1990s [5].
According to ‘‘the state of the art,’’ there was a pressing need to consider the morphological complexity of cells and tissues by using a systemic approach, whilst at the same time developing instruments that could enable the accomplishment of that goal without introducing any shape approximation or smoothing, a condition which could not be satisfactorily achieved with conventional analytical methods. In fact, the latter situation which relied on conventional disciplines such as morphometry and stereology yielded experimental data relating to the quantitative description of membranes that was usually controversial. This left many questions unresolved and thereby prevented a true consensus being reached among the investigators. To highlight the striking debate that led to such turmoil within the biologist community, it might suffice to report the original description, of the first case study conducted several years earlier [6]. This related to the application of fractal geometry in cell biology; notably, the discovery that cellular membrane systems have fractal properties arose from the uncertainty of observations regarding the extent of such membranes. When the results of the first studies on the morphometry of liver cell membranes were reported, the values obtained were much higher than had been reported by others. There followed much debate as to which of these estimates was correct, and whether liver cells contained 6 or 11 m2 of membranes per cm3, a quite significant difference. The question was also raised as to whether the stereological methods used were reliable, since it appeared possible that the same method might yield different results if the measurements were made under different magnifications of the electron micrographs. Ultimately, the systematic measurement of liver cell membranes revealed that the estimates of surface density increased with increased resolution. Shortly after the conclusion of the experimental phase, Mandelbrot suggested that the results should be interpreted with the likely effect of the ‘‘resolution scale,’’ in analogy with the ‘‘Coast of Britain effect’’ [4]. The estimate discrepancy was resolved allowing to explain why measurements of irregular liver cell membranes at higher magnification yielded higher values than were obtained at lower magnification [6]. It must be stressed here that the scaling effect applies mainly to cellular membranes with a folded surface or an indented wrinkled profile, such as the inner mitochondrial membrane. In contrast, measurement of the surface density of the outer mitochondrial membrane, which is almost smooth, was only slightly affected by the resolution effect. Several authors further addressed the problem relating boundary length to resolution, namely with regard to specimens showing ‘‘non-ideally fractal’’ dimensions such as lung tissues but also to cell tissues in different physiopathological conditions [5].
Founded upon a body of well-defined laws and coherent principles, including those derived from chaos theory, the Fractal Geometry allows the recognition and the quantitative description of complex shapes, living forms, biologic tissues, organized patterns of morphologic features correlated through a broad network of functional interactions and metabolic processes that shapes the adaptive response and makes the accomplishment of life possible [5]. Obviously, this came in opposition to the ancient vision based on the rules of the Euclidean geometry and widely adopted concepts, such as homeostasis, linearity, smoothness and thermodynamic reversibility, which emanate from a cultural view but ideal of envisaging things and facts. Later on it has become evident that biologic elements, unlike deterministic mathematical structures, express statistical self-similar patterns and fractal properties within a defined interval of scales, called “scaling window ", in which the relationship between the observation scale and the measured size or length of the object can be established and defined as the fractal dimension [FD] [3]. The fractal dimension FD of a biological component remains constant within the scaling window and serves to quantify the variation in length, area or volume with changes in the size of the measuring scale. The recourse to the principles of fractal geometry has enabled to reveal that most biological elements, either at cellular, tissue or organic level, have self-similar structures within a defined scaling domain which can be characterized by means of the fractal dimension FD. However, concrete "fractality" exists only when the experimental scaling range accounts for at least two orders of magnitude, namely spans two decades on the scaling axis. Data spanning several decades of scale has been previously reported in many other fields: thus, defining a “scaling range” appears as an inescapable requisite for assessing the fractality of every biological element. Its occurrence will hence exclude any ambiguous assignment and so far strengthen the statement of Mandelbrot «Fractals are not a panacea; they are not everywhere». In the Epilog of his work -The path to fractals- he wrote «The reader knows well that the probability distribution of fractals is hyperbolic, and that the study of fractals is rife with other power law relationships». Nowadays, the Fractal Geometry provides the theoretical and methodological framework for unravel temporal processes and complex biological structures, as underlined by the increased frequency of outstanding publications, what definitely reinforces a valiant sentence written more than twenty years ago «Fractal Geometry: a Design Principle for Living Organisms» [7]. So far, it is worthy to point out that the fractal dimension is a statistical measure which correlates the morphological structural complexity of cellular components and biological tissues. It is also a numerical descriptor which serves to measure qualitative morphological traits and self-similar properties at various levels, cellular, tissue or organic. Mandelbrot stated in his book that «A fractal set is a set in metric space for which the Hausdorff-Besicovitch dimension D is greater than the topological dimension DT». In Nature, a fractal object is defined by its structural properties, namelyby surface rugosity and irregularity or absence of smoothness, form invariance on scaling, self-similarity, morphostructural and functional complexity.The Richardson-Mandelbrot equation provides the mathematical basis for understanding geometric and spatial fractal structures, and for measuring and interpreting them, namely
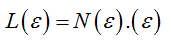 (1)
(1)
where L(ε) represents the contour length (e.g. the perimeter) of the biological component under investigation, (ε) the unit length of measure and N(ε) the number of unit lengths (ε) needed to cover the contour L(ε). By substituting N(ε) with [loDε-D] into (1), the above equation can be transformed by logarithmic procedure and rewritten as
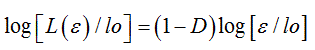 (2)
(2)
which is the equation of a straight line with slope 1-D, from which the dimensional exponent D can be calculated to yield the numerical value of the fractal dimension FD. As mentioned in the Introduction, biological fractals also called asymptotic natural fractals show auto-similar scaling properties (fractality) within a fractal windows, graphically represented by the region II in the middle of three typical regions, limited by a lower (εmin) and an upper bound (εmax), of a bi-asymptotic fractal, where a straight line can be drawn and the fractal dimension [FD] calculated from its slope. While the practical evaluation of the fractal dimension could be obtained by various quantitative approaches, the box counting method easily based on counting of the non empty boxes N at a variable grid length (ε), is by far the most reliable.
Particularly at the electron microscopy level, the fractal analysis proved useful for an objective investigation of cell shape and cell phenotype, the fine cytoplasmic structures and the organization of cell membranes and nuclear components and other subcellular organelles, either in normal or pathological tissues and in cell cultures during time. The fractal tool has also been employed to document the feasibility of using ultrastructural changes in cell surface and nuclear inter(eu)chromatin to assess the early phases of apoptotic cell death. Ultrastructural changes which involved a loss in heterochromatin irregularity due to its increased condensation (lower FD), were evident well before the detection of conventional cell markers, which were only measurable during the active phases of apoptosis [8]. Furthermore, the nuclear complexity of human healthy lymphocytes was shown to undergo a reduction of FD during the apoptotic process. Measuring the FD of euchromatin and heterochromatin nuclear domains helped to discriminate lymphoid cells found in Mycosis fungoides from those in chronic dermatitis [5]. It has been observed that the complex structure of the living cell is critical for cellular function and that the spatial organization of the cell is even more important for cellular properties than is its genetic, epigenetic, or physiological state. Yet relatively little is known about the mechanisms that produce the complex spatial organization of a living cell [9].
For an objective description of neoplastic and pathologic traits of cell tissues by the fractal approach, the main condition is the experimental definition of a scaling interval rather than a unique dimensional scale selected a priori. A critical reading of the literature shows that such a distinctive characteristic is insufficiently taken into account and inadequately applied in many investigations. These views are typically interpreted in a qualitative manner by clinicians trained to classify abnormal features such as structural irregularities or high indices of mitosis. A more quantitative and hopefully more reproducible approach, which may serve as a useful adjunct to trained observers, is to analyze images with computational tools. Herein lies the potential of fractal analysis as a morphometric measure of the irregular structures typical of tumor growth. Among the most promising fields of investigation, for which fractal geometry provides an original approach and fractal dimension represents more than an additional geometrical parameter or just “a useful adjunct” are cell heterogeneity, architectural organization of tissues tumor, parenchymal border, cellular/nuclear morphology, developmental and morphogenetic processes in tissues and organs in healthy, pathologic, or tumor conditions, and the pathologies of the vascular architecture. Tumor grading on histology specimens is difficult to assess because tumors often consist of a heterogeneous mixture of cells with varying degrees of irregularity as well as local variations in cellular differentiation. Measuring the fractal dimension could aid pathologists in grading heterogeneity and in determining the spatial extent of poorly differentiated regions of breast and prostate tumors [10]. Cell heterogeneity, known to contribute in a determinant way to the histological grading of human breast cancer, has been examined by means of geostatistics and the Hurst fractal parameter [11]. Several examples seem to indicate that the occurrence of morphogenetic dynamics, the emergence of complex patterns, and the architectural organization of active tissues and tumor masses may be driven by constructive mechanisms related to fractal principles, including deterministic and/ or random iteration of constituent units with varying degrees of selfsimilarity, scaling properties, and form conservation. Preservation of tissue architecture and cell polarity of organs and the eventual restoration of organized traits in tumor tissues, deconstructed and deregulated at various levels, is an emerging field of interest since it has been observed that biological entities organize with their own degrees of structural and behavioral complexity, develop on different spatial and time scales and follow modifications induced by drug or endocrine treatment as well. It has been argued that reversion into a more ‘‘physiological’’ fractal dimension implies reduced morphologic instability and an increase of cells connectivity, what emphasizes the relevance of shape fractal parameters as descriptors of cell transition from one phenotype to another. Fractal dimension has been used as a characterization parameter of premalignant and malignant epithelial lesions of the floor of the mouth in humans and of architectural changes of the epithelial connective tissue interface (ECTI) of the buccal mucosa during aging [12]. The onset of fundamental phenomena such as development, growth and cell death during different stages of carcinogenesis and cell differentiation, i.e., from mesenchymal to smooth muscle cells, has been adequately investigated by fractal geometry. One highly promising approach appears to be a combination of fractal analysis, that provides a quantitative description of shapes, with radiographic images able to discriminate malignant from benign tumor masses, and also from normal tissue structures. The computed FD of the contour of a mass may be useful for characterizing shape and gray-scale complexity, which may vary between benign masses and malignant tumors in mammograms [13].
The original conception of Galeno (Pergamo, 129-216 D.C.) that confined the superior functions of brain within three cerebral cells (spheres), has spanned several centuries up to the Renaissance period culminating with Leonardo da Vinci (1452-1519). As pointed out in an exhaustive review [2] the first outstanding breakthrough in the brain knowledge was accomplished by Andreas Vesalius with his famous work “ De humani corporis fabrica” (1543); cerebral surface convolutions were described without a detailed identification of inner morphological pattern. Nevertheless he conjectured a probable link between brain structures and psychological functions. Relevant investigations were successively performed by Marcello Malpighi (1628-1694) who suggested the existence of a nervous fluid filling in cerebral glands, by Thomas Willis (1621-1675) who evidenced an arterial circuit by anastomosis of internal carotids and vertebral artery, and by Vicq d’Azyr (1746-1796) who revealed convolutions in unidentified areas of the external brain surface. Albrecht von Haller (1708-1777) had also conjectured the existence of a secretive function. Franz Joseph Gall (1758-1828) and Johann Spurzheim (1776- 1828) identified phrenological maps sharing specific brain functions. Later on, Paul Broca (1824-1880) localized cerebral zones with specialized activities such as those for the language arguing that “Nous parlons avec l‘hémisphère gauche”. Carl Wernicke (1848-1905) identified an area in the temporal lobe, whose damage may provoke the selective loss of the capacity of listening words. Within the late 19th and the early 20th centuries, there appeared the outstanding contributions of two coeval scientists, both Nobel Laureates: Camillo Golgi (1843-1926) who postulated the “reticular theory” suggesting that the nervous system is a syncytial system of nervous fibers that forms an intricate complex diffuse network along which the nervous impulse may propagate. On the other side Santiago Ramón y Cajal (1852-1934) developed the “neuron theory” for which the relationship between nerve cells was not one of continuity, but rather of contiguity, accomplished through small membranous spines protruding from neuron’s dendrites that typically receive input from a single synapse of an axon (output). In the last decades the implementation of performant imaging techniques, such as Positron Emission Tomography (PET), Functional Magnetic Nuclear Resonance (fMNR), Computed Axial Tomography (CAT), etc. in concomitance with the increment of the theoretical knowledge provided by the innovative Fractal geometry and modern Mathematics have opened an unprecedented analytical breakthrough. Actually, digital images recovered from body sequential cross-sections according to the Cavalieri’s principle for volume determination enabled to combine the close representation of whole structures with the fractal quantitative evaluation of their anatomical/morphological peculiarities. The evolutionary concourse of two major events, i.e., “the tremendous expansion and the differentiation of the neocortex”, has contributed to the development of the human brain [14]. Today, modern neurosciences recognize the presence of fractal properties in brain at various levels, i.e., anatomical, functional, pathological, molecular, and epigenetic, but not so long ago there was no analytical method able to objectively describe the complexity of biological systems such as the brain. The intricacy of mammalian brain folds led Mandelbrot to argue that «A quantitative study of such folding is beyond standard geometry, but fits beautifully in fractal geometry». At that time however, there was no certainty about the brain’s geometry or about neuron branching. Anatomical-histological evidence that the complexity of the plane-filling maze formed from dendrites of neural Purkinje cells of cerebellum was more reduced in non-mammalian species than in mammals led Mandelbrot to comment: «It would be very nice if this corresponded to a decrease in fractal dimension (FD), but the notion that neurons are fractals remains conjectural» affirmed Mandelbrot [1]. Since then, a wealth of investigations have documented the fractal organization of the brain and nervous tissue system, and implication of fractals for neurosciences has been unambiguously affirmed. Among relevant applications of fractal analysis to nervous and brain tissue were pioneering studies which showed that the fractal dimension is an unbiased measure of the complexity of neuronal borders and branching pattern and of the time course of morphological development and differentiation of spinal cord neurons in culture, increasing from 1.1 for the less differentiated neuron up to 1.5 for the most differentiated cell. Further studies have confirmed that the fractal dimension correlates with the increase in morphological complexity and neuronal maturity. In some recent reports, rather exciting, it ha been argued that there is a trend towards a “Unified Fractal Model of the Brain” [15]. These authors suggested that the amount of information necessary to build just a tiny fraction of the human body, that is, just the cerebellum of the nervous system, was a task for which 1.3% of the information that the genome could contain was totally insufficient. «Fractal genome grows fractal organism; yielding the utility that fractality, e.g. self-similar repetitions of the genome can be used for statistical diagnosis, while the resulting fractality of growth, e.g. cancer, is probabilistically correlated with prognosis, up to cure» [15]. The brain is now accepted as one of nature’s complete networks, while the hierarchical organization of the brain, seen at multiple scales from genes to molecular micronetworks and macronetworks organized in building neurons, has a fractal structure as well with various modules that are interconnected in small-world topology. The theoretical significance is that the fractality found in DNA and organisms, for a long time “apparently unrelated,” was put into a “cause and effect” relationship by the principle of recursive genome function [16,17].
Fractal analysis was applied to anatomical/ histological images and high-resolution magnetic resonance images in order to quantify the developmental complexity of the human cerebral cortex, the alterations in diseased brain with epilepsy, schizophrenia, stroke, multiple sclerosis, amyotrophic lateral sclerosis (ALS), cerebellar degeneration, and the morphological differentiation of the peripheral nervous .FD values estimated for brain white matter (WM) skeleton, surface and general structure in both controls and ALS patients revealed no significant WM changes between controls and ALS patients and among the AL5 subgroups. A highly significant reduction of the fractal dimension was observed in the cortical ribbon of Alzheimer’s Disease patients with respect to control subjects [18]. The 3-D fractal dimension of the Purkinje neurons decreased from 1.723 to 1.254, indicating a significant reduction of dendritic complexity during cortical development disorder. The fractal analysis has enabled to quantitatively describe the complex morphological forms in which astrocytes occur in brain of ischemic/hemorrhagic stroke and Alzheimer’s disease (AD). In contrast, fractal dimension values were found higher in the Gray Matter (GM) of Multiple Sclerosis patients (MS) compared to controls and indicated that GM tissue in MS has higher morphological complexity, perhaps due to the presence of the inflammatory component (i.e., microglia activation) and cellular changes in the GM. In large neurons of the human dentate nucleus the fractal dimension [FD] has been found to correlate with the increase in morphological complexity and neuronal maturity. Lastly, a quantitative evaluation of the surface fractal dimension may allow not only to measure the complex geometrical architecture, but also to model the development and growth of tumor neovascular systems and explore the morphological variability of vasculatures in nature, in particular the microvasculature of normal and adenomatous pituitary tissue. The fractal analysis was recently applied on patients with cerebral arterial venous malformations (AVM): increased FD values related to structural vascular complexity were due to the increased number of feeding arteries in patients suffering from AVM. In the normal human retina, blood vessels or vascular trees exhibited an FD of 1.7, the same fractal dimension found for a diffusion- limited growth process, a finding which may have implications for the understanding of the embryological development of the retinal vascular system. In large neurons of the human dentate nucleus the fractal dimension [FD] has been found to correlate with the increase in morphological complexity and neuronal maturity. A recent study described a method for quantifying cerebral blood flow (CBF) distribution in Alzheimer’s disease (AD) from Single Photon Emission Computer Tomography (SPECT) images obtained with Technetium (99mTc) exametazime (HMPAO) by 3-dimensional fractal analysis (3D-FA). The fractal dimension 3D-FA was well correlated with the cognitive impairment, as assessed in neuropsychological tests and could represent a useful method for objectively evaluating the progression of AD.
The human brain was buried for centuries and considered a black box remaining hidden from any experimental scientific investigation, in reason of a dominant philosophical thought and aesthetic perception combined with the lack of an adequate methodology. Nowaday, the brain can be observed in vivo whereas a subject is undertaking many different cognitive or motoric tasks by examining neuroimages obtained with recent developed methodologies, such as TAC, fNMR, NMR, PET, SPECT. Nevertheless an enormous challenge remains to be solved in the future, namely the features and the structures revealed by neuroimages should be submitted to a stringent quantitative analyse i.e., evaluated by a scaling free fractal approach that takes into account shape complexity and morphological richness thus preventing any approximation or smoothing of peculiar features. It has been observed that, in concomitance with genetic heritage, some factors such as volume and functional changes of amigdala might intensify the propensity level toward an aggressive behaviour by abused children. Recently, neuroimaging techniques have indicated that the increase in white matter of corpus callosum, the reduction of gray matter in the prefrontal cortex or the decrease of the posterior Hippocampus volume may compare in many individuals with antisocial conduct [19]. A stereological report has revealed that violent mentally disordered individuals suffer from a significant anterior cingulate volume loss [20]. Despite the evidence brought by the experimental yet conventional studies quoted above, there is no doubt that a definite assessment can only be obtained by measuring complex traits during time, namely by means of the fractal geometry.
While the complexion of brain and nervous tissue remains largely understood, the present survey provides experimental data confirming that biological processes including growth, proliferation, apoptosis, epigenetic and genetic mechanism, morphologic/ultrastructural and functional organization occurring in living elements and complex organized tissues may follow fractal rules. Among the main fractal peculiarities worth noticing is the process of iteration, whose powerful dynamics allows specific generators to be properly iterated at different scales (small and large) without a priority choice, by linking efficient genetic programming in order to achieve the formation of viable biological forms and living objects. The large agreement with the fractal nature of the brain and nervous cell system, sustained by theoretical experimental and heuristic foundations, is nowadays consolidated and intervenes more than thirty years after the publication of the Fractal Geometry of Nature, in which Mandelbrot recognized that «the notion that neurons are fractals remains conjectural». Its relevance and contribution to the cultural development of mankind (as comprehensive of humanistic and scientific thinking) is keen underlined by the observation of some years ago arguing that the fractal geometry could be considered as a biological design principle for living organisms [7]. More recently it was reported that «fractals would surely be a most extraordinary design principle for operational economy in complex systems» [21]. The experimental evidence indicates that the majority of complex biological shapes and structures could be depicted as fractal entities: hence, fractal analysis is the most valuable tool for measuring dimensional, geometrical and functional parameters of cells, tissues and organs that occur within the animal and vegetal realms. In a comprehensive treatise dedicated to fractal geometry of brain it has been alleged that «fractals have definitively entered into the realms of clinical neurosciences» [22]. Now we just have to hope that even forensic neurosciences will fully benefit from the fractal geometry with its theoretical and methodological background in order to unpack complex brain relics.
- Mandelbrot B (1983) The Fractal Geometry of Nature. Freeman, San Francisco.
- Mandelbrot B (1977) Fractals, M.B. Form, Chance and Dimension. 1977. W.H. Freeman and Company, San Francisco.
- Losa GA, Nonnenmacher TF (1996) Self-similarity and fractal irregularity in pathologic tissues. Mod Pathol 9: 174-182. [Crossref]
- Mandelbrot B (1967) How long is the coast of britain? Statistical self-similarity and fractional dimension. Science 156: 636-638. [Crossref]
- Losa GA (2012) Fractals in Biology and Medicine. In: Meyers R (Ed.), Encyclopedia of Molecular Cell Biology and Molecular Medicine. Wiley-VCH Press, Berlin.
- Paumgartner D, Losa G, Weibel ER (1981) Resolution effect on the stereological estimation of surface and volume and its interpretation in terms of fractal dimensions. J Microscopy 121: 51-63. [Crossref]
- Weibel ER (1991) Fractal geometry: a design principle for living organisms. Am J Physiol 261: L361-369. [Crossref]
- Losa GA, Castelli C (2005) Nuclear patterns of human breast cancer cells during apoptosis: characterization by fractal dimension and (GLCM) co-occurrence matrix statistics. Cell Tissue Res 322: 257-267. [Crossref]
- Marshall WF1 (2011) Origins of cellular geometry. BMC Biol 9: 57. [Crossref]
- Losa GA (2015) The Living Realm depicted by the Fractal Geometry. Fractal Geometry and Nonlinear Anal in Med and Biol 9: 57-66.
- Sharifi-Salamatian V, Pesquet-Popescu B, Simony Lafontaine J, Rigaut JP (2004) Index for spatial heterogeneity in breast cancer. J Microsc 216: 110-122. [Crossref]
2021 Copyright OAT. All rights reserv
- Landini G, Hirayama Y, Ti L, Kitano M (2000) Increased fractal complexity of the epithelial-connective tissue interface in the tongue of 4NQO- treated rats. Pathol Res Practice 196: 251-258. [Crossref]
- Rangayyan RM, Nguyen TM (2007) Fractal analysis of contours of breast masses in mammograms. J Digit Imaging 20: 223-237. [Crossref]
- De Felipe J (2011) The evolution of the brain, the human nature of cortical circuits, and the intellectual creativity. Front Neuroanat 5: 1-16. [Crossref]
- Di Ieva A, Grizzi F, Jelinek H, Pellionisz AJ, Losa GA (2014) Fractals in the Neurosciences, Part I: General Principles and Basic Neurosciences. Neuroscientist 20: 403-417. [Crossref]
- Pellionisz AJ (2008) The principle of recursive genome function. Cerebellum 7: 348-359. [Crossref]
- Pellionisz A (1989) Neural geometry:towards a fractal model of neurons. Cambridge: Cambridge University Press.
- King RD, Brown B, Hwang M, Jeon T, George AT; Alzheimer's Disease Neuroimaging Initiative (2010) Fractal dimension analysis of the cortical ribbon in mild Alzheimer's disease. Neuroimage 53: 471-479. [Crossref]
- Yang Y, Glenn AL, Raine A (2008) Brain abnormalities in antisocial individuals: implications for the law. Behav Sci Law 26: 65-83. [Crossref]
- Kumari V, Uddin S, Premkumar P, Young S, Gudjonsson GH, et al. (2014) Lower anterior cingulate volume in serious violent men with antisocial personality disorder or schizophrenia and an history of childhood abuse. Aust N Z J Psychiatry 48: 153-161. [Crossref]
- Werner G (2010) Fractals in the nervous system: conceptual implications for theoretical neuroscience. Front Physiol 1: 15. [Crossref]
- Di Ieva A (Ed.) (2016) The Fractal Geometry of the Brain. ISBN 978-1-4939-3995-4, 1st ed. XXII, 585.

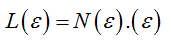 (1)
(1)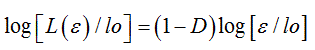 (2)
(2)