Abstract
The adsorption of fluoride from aqueous solution onto synthesized hydroxyapatite is investigated in the present study. Hydroxyapatite is the cost effective and most efficient adsorbent, which is synthesized by co-precipitation method. Structure is characterized by FTIR, XRD methods. The Langmuir adsorption isotherm, Freundlich adsorption isotherm were used to explain adsorption between the liquid and solid phases in batch studies. The mechanism of adsorption process was illustrated by calculating Gibbs free energy, enthalpy and entropy from thermodynamic studies. This experiment was conducted to investigate the interaction of process parameters using response surface methodology(RSM). The two level three factor(23) central composite design(CCD)with the help of Design Expert Software was used to optimize process parameters. The higher correlation coefficient(R2) value of 0.9671 indicates the fitness of response surface quadratic model. By using multiple numerical optimization, desirability function is achieved, which is used to identify the optimum conditions. The optimum removal efficiency of HAP for fluoride adsorption is 89.6% at optimum condition.
Key words
fluoride adsorption, calcium hydroxyapatite, response surface methodology, adsorption isotherm, adsorption kinetics, thermodynamic parameters
Introduction
According to the World Health Organization the maximum acceptable concentration of fluoride ions in drinking water is below 1.5 mg/l. As fluoride ion is negatively charged so it is attracted by positively charged calcium ion in teeth and bones. As a result of high fluoride ingestion by children as well as adults, fluorosis is found in mild version and high version. The fluoride is removed from contaminated water is by liming and following precipitation of fluoride in conventional method. There are various other methods used for the de-fluoridation [1,2] of water such as ion-exchange precipitation, reverse osmosis and electro coagulation.
Adsorption [3,4] is defined as the phenomenon where particular substance in solvent is deposited on the surface of solid adsorbent which has affinity towards that substance. In this case, the solid adsorbent is chemically synthesized product; calcium hydroxyapatite(Hap) [5]. In chemisorption, the gas molecules or atoms are held to the solid surface by chemical bonds which are covalent or ionic in nature.
Calcium Hydroxyapatite, [Ca10(PO4)6(OH)2] is widely used in different purposes. So it has various application in different fields such as catalysis, fertilizers, protein chromatography, water treatment process and preparation of artificial bones and teeth [6]. In the scientific community there are various chemical methods for synthesis of Hap such as precipitation, micro-emulsion, microwave irradiation or hydrothermal method. At this phase of Hap main difficulties are (a) formation of non-stoichiometric products, (b) low crystallinity due to improper pH, temperature and (c) contamination of the reactants because the ions of the reactants(nitrate, chloride) have strong affinity towards Hap. The precipitation process is the most extensively used method for preparation Hap. This method is very suitable for industrial production. Due to existence of property such as substitution, it is very common for the existence of stoichiometric hydroxyapatite. As the hydroxyl group in Hap is substituted by chloride, fluoride and carbonate, so defects can also exist which results the deficient hydroxyapatites. Hap has capability to integrate in bone structures and support bone in growth, without breaking down or dissolving. It is a thermally unstable compound because it decomposes at temperature from about 800-1200°C depending on its stoichiometry. Usually in absence of the mechanical strength it is unable to succeed in long term load bearing applications.
The crystal and solution chemistry of Hap has been highlighted mostly by biological and earth scientists but studies of the electrochemistry of apatite surfaces is not extensively applied. Structure of Hap consists of calcium surrounded by phosphate and hydroxyl groups. The few studies of the surface charge characteristics of hydroxyapatite [Ca10(OH)2(PO4)6] and fluorapatite [Ca10F2(PO4)6] show that H+ and OH− are potential determining ions, but determination of pH at the point of zero charge (PZC) widely varied from 4.3 to 7.6 for hydroxyapatite and from 4 to >12 for fluoroapatite.
Naturally waters may contain various amounts of fluoride. Consumption of fluoridated water approximately 1 mg/liter is very effective in reducing tooth decay. Excessive exposure to fluoride results fluorosis. De-fluoridation methods those are already proposed are divided into two groups (a) precipitation methods and (b) adsorption or ion exchange method which are regenerated and reused [7-11]. The most popular method for de-fluoridation is Nalgonda technique [12] which is used in many countries. Adsorption technique is the most cost effective method for de-fluoridation [13-15].
The earliest proposed method for the removal of fluoride from water is the use of degreased bone. The carbonate radical which is present in bone, replaced by anion exchange with fluoride to form fluorapatite. By utilizing the strongest alkali(caustic soda), fluorapatite is chemically converted to hydroxyapatite and the fluoride is removed as soluble sodium fluoride (NaF). The hydroxy radical (OH.) in Hydroxyapatite is replaced by fluoride. In the controlled conditions the chemical reaction is occurred between phosphoric acid and lime which results the formation of tri-calcium phosphate and hydroxyapatite. Within the mixing basins of a conventional treatment plant the above reaction takes place with flocculation, sedimentation, and filtration.
Objective of this work
The main objective of the present study is to determine the optimum conditions for de-fluoridation by adsorption in aqueous system. The application of statistical experimental design techniques in adsorption process can result in improved product yields, reduced variation in process parameters, closer confirmation of the output response to nominal and target. In this study, the combined effects of adsorbent dose, pH, temperature on fluoride removal from aqueous medium by hydroxyapatite were investigated using CCD(Central Composite Design) in response surface methodology (RSM) by Design Expert Version7.0.6.1 (Stat Ease, USA). The mechanism of sorption by Hap was thermodynamically [16] studied by estimation of different factors such as Gibbs free energy, entropy, enthalpy.
Material and methods
Materials
Calcium nitrate [Ca(NO3)2.4H2O](Merck, Germany), Di-ammonium hydrogen phosphate [(NH4)2HPO4](Merck, Germany) and Ammonia (25% aqueous solution) were used for preparation of Hap. All the chemicals were reagent grade and ultrapure deionized water were used in all the preparations.
Preparation of adsorbent(Hap)
1 M of Ca(NO3)2.4H2O and 0.6 M of (NH4)2HPO4 were dissolved in ultrapure water separately. To avoid contamination, 25% ammonia solution was added drop-wise at 80°C to prevent the carbonation into a 1 M Ca(NO3)2 solution to achieve pH value approximately to 11. The 0.6 M (NH4)2HPO4 solution was added drop-wise and stirred vigorously for 1 hour, which results milky white precipitate. The stirred solution was firstly maintained at 80°C for 1 hour and then at 37°C for 24 hours. Then the precipitate was vacuum filtered by Millipore membrane (0.2 μm) and then it was washed with water to remove residues of ammonia and nitrate ions. These ions were qualitatively detected by different chemical test. Then the precipitate was dried at 50°C in a vacuum oven. According to the following reaction by precipitation method Hap was chemically synthesized [17,18] as follows:
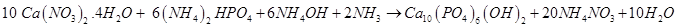
Preparation of synthetic fluoride solutions
Sodium fluoride was used in this study. Stock fluoride ion solution (1000 mg L-1) was prepared by dissolving accurately weighed quantity in double-distilled water. Experimental fluoride solution of different concentrations were prepared by diluting the stock solution with suitable volume of double -distilled water.
Experimental procedure
Batch experiments
For batch experiments, 100 ml fluoride solutions of concentration 50 ppm(mg L-1) were taken in 250 mL PTFE(Polytetrafluoroethylene) conical flasks. The particular weighed amount of adsorbent was added to each solution. Then the flasks were agitated at 150 rpm in an incubator shaker at different temperatures. The effects of contact time (1, 5, 10, 15, 25, 30, 40, 45, 50 and 60 min), adsorbent dose (0.2, 0.5, 0.75, 1, 1.25, 1.5, 2 g) and temperature (303, 308, 313, 318, 323, 328 and 333K) were evaluated during the batch studies.
Experimental setup
Experiments were conducted in temperature controlled incubator shaker (INNOVA 4430, New Brunswick Scientific, Canada). Temperature fluctuations in the reactor was negligible. After shaking for particular time intervals those samples were collected from the flasks for analysis of fluoride concentration in the solution. The residual amount of fluoride in each conical flask was estimated by using ion-meter(Thermo Scientific Orion ion-meter, USA).
Thermodynamics and kinetics study
Adsorption isotherm
Freundlich isotherm
Freundlich proposed an empirical mathematical equation as follows:
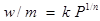 …………………………………………………………………(1)
…………………………………………………………………(1)
where wis the mass of the solute adsorbed on a mass m of adsorbent at a pressure P; kand nare constants depending on the nature of the solute and the adsorbent and on temperature.
This relation is generally represented in the form of a curve obtained by plotting the mass of the gas adsorbed per unit mass of adsorbent (w/m) against equilibrium pressure. Freundlich isotherm is not applicable at high pressures.
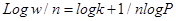 ………………………………………………………….(2)
………………………………………………………….(2)
The Freundlich isotherm constants are estimated using the following equation:
 …………………………………………………………..(3)
…………………………………………………………..(3)
Where Qe is the amount of fluoride adsorbed at equilibrium, and KF and n are Freundlich constants related to adsorption capacity and adsorption intensity respectively.
Langmuir isotherm
The following equation is used as follows:
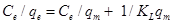 ………………………………………………………………(4)
………………………………………………………………(4)
Where qe is the amount of fluoride adsorbed at equilibrium (mg/L), Ce is the concentration of fluoride in the aqueous phase at equilibrium (mg/L). KL and qm are the Langmuir constants related to energy of adsorption and the adsorption capacity.
Adsorption kinetics
The adsorption process is investigated at various temperatures to determine the optimum temperature for maximum adsorption efficiency and for obtaining the reaction rate constant and activation energy. 100 ml of fluoride solution of concentration 50 mg/L is taken in PTFE conical flask and 1 g/L adsorbent is added to it. Then this mixture is agitated at 150 rpm for 1 hour. From this experiment mathematically kinetic rate constant at different temperatures is calculated.
Pseudo-first order kinetic model
The pseudo-first-order rate constant is estimated using the following equation:
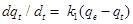 ……………………………………………………….(5)
……………………………………………………….(5)
where, qe=amount of fluoride adsorbed at equilibrium/unit weight of adsorbent (mg/g), qt is the amount of fluoride adsorbed at any instant (mg/g) and k1 is the rate constant (min−1).
Integrating and applying boundary conditions as t=0 and qt=0 to t=t and qt=qt, the final Equation is:
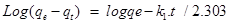 ………………………………………….(6)
………………………………………….(6)
Pseudo-second order kinetic model
The pseudo-second-order kinetic model equation is described as follows:
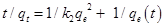 …………………………………………………….(7)
…………………………………………………….(7)
Where k2 denotes the pseudo-second-order rate constant of adsorption (g mg–1 min–1) and qe and qt are the amounts of fluoride adsorbed (mg/g) at equilibrium and at time t respectively.
Activation energy
From obtained the rate constant, activation energy of the adsorption of fluoride is calculated using Arrhenius Equation (8) given as follows:
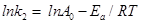 ……………………………………………………..(8)
……………………………………………………..(8)
Where Ea=activation energy (kJmol−1); R=gas constant (8.314 J mol−1 K−1); and A0=Arrhenius constant.
Adsorption thermodynamics
The thermodynamics parameters of fluoride adsorption is estimated using the following formulas:
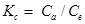 …………………………………………………………….(9)
…………………………………………………………….(9)
where Kc=coefficient of distribution for the adsorption; Ca=fluoride adsorbed per unit mass of the adsorbent (mg L−1); Ce=equilibrium concentration of adsorbate in aqueous phase (mg L−1).
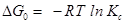 ……………………………………………………….(10)
……………………………………………………….(10)
where G0 (kJ mol−1)=change of Gibb’s free energy; R= universal gas constant; and T=absolute temperature (K); and
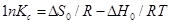 ………………………………………………(11)
………………………………………………(11)
where ΔH0 (kJ mol−1)=change of enthalpy; ΔS0(J mol−1 K−1)=change of entropy.
Response surface methodology for optimization of adsorption parameters: The determination of optimum conditions for fluoride adsorption by Hap depends on the three process variables, which are adsorption dose, temperature and pH of the solution. The experimental ranges along with the levels of variables are given in Table 1. The percent removal of fluoride is the response of the system. Statistically the prediction of the optimum condition is obtained following the quadratic equation model given below (Eq. 12).
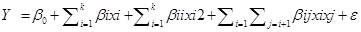 ……………………(12)
……………………(12)
Here, Y=response (i.e., dependent variable), β0= constant coefficient, βi=βii=βij=coefficients of linear, quadratic and interaction effect, xi and xj=factors (independent variables)
and ε =error.
Percent removal of fluoride is estimated with a standard RSM design (CCD) [19,20]. 20 experiments are performed which is described in Table 2. The percent removal (%) of fluoride is determined by using the following equation (13):
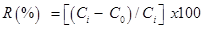 ……………………………………………………….(13)
……………………………………………………….(13)
where Ci is the initial fluoride concentration (mg L-1) and C0 is the final fluoride concentration in solution (mg L-1).
Design Expert Version 7.1.6 (Stat Ease, USA) is utilized for regression and graphical analysis of the experimentally obtained data. The optimum values of the independent variables are obtained by solving the regression equation and by analyzing the response surface contour plots. The variability in response is statistically explained by the multiple coefficient of determination. The correlation of coefficient and the quadratic model equation is used to predict the optimum value, from which the interaction effect of different factors within the specified range is described vividly.
Statistical analysis
In order to maintain quality assurance, the precision, accuracy, repeatability and reproducibility
of the obtained experimental data, all experiments are performed thrice, and the mean values are expressed in data analysis. The calculated relative standard deviations within ±2%.
Table 1. Experimental range and levels of independent variables
Serial no |
Variable |
Unit |
Notation |
Range and levels(coded) |
–α |
-1 |
0 |
+1 |
+α |
(1) |
Adsorbent dose |
g |
A |
0.33 |
0.5 |
0.75 |
1.0 |
1.17 |
(2) |
pH |
|
B |
0.3 |
2 |
4.5 |
7 |
8.7 |
(3) |
Temperature |
K |
C |
306.18 |
313 |
323 |
333 |
339.82 |
Results and discussion
Characterization of HAP
FTIR(Fourier Transformed Infrared Spectroscopy): Functional groups present on the Hap is identified by Fourier transform infrared (FTIR) spectroscopy as each group has a unique energy absorption band. So FTIR spectra were recorded using FTIR spectrophotometer (Spectrum BX, Perkin Elmer) in the wavenumber range 4000–500 cm-1 at 4 cm-1spectral resolution. FTIR spectra of the prepared HAP were depicted in Figure 1. It is proved that the broad band at 3431 cm-1 appears from hydroxyl stretching and librational modes of OH- due to the presence of hydrated layer along with HAP. The carbonate band(CO32-) (as impurity) appears at 1422 cm-1 due to the sample preparation in the atmosphere. As a result carbonate ion replace (PO43-) ion in HAP lattice. Also, the band appears at 1463 cm-1 due to (OH-)bond in HAP lattice structure. The presence of two distinct bands at 603 and 567 cm-1 were due to symmetric P-O stretching vibration of (PO43-) which support the formation of hexagonal hydroxyapatite. Besides this an absorption bands arises at 1036 cm-1was due to asymmetric stretching modes. The presence of peak in the region 1400–1450 cm−1 was due to carbon-dioxide. The sharp peaks belonging to the hydroxyl and phosphate groups in FTIR spectrum of HAP sample confirm the crystallized apatite structure [21].
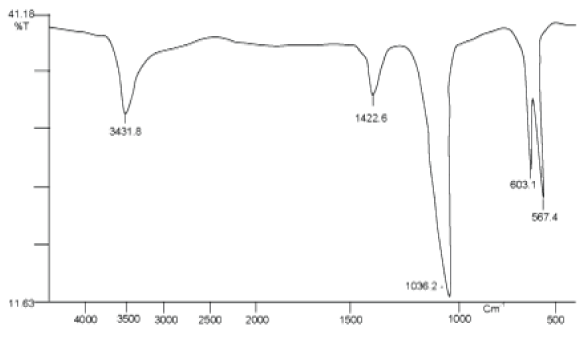
Figure 1. FTIR spectrum of HAP calcined at 673K
XRD(X-Ray Diffraction) analysis: X-ray diffraction analysis of the adsorbent was carried out using X-ray diffractometer equipment with a Cu Kα radiation. The XRD pattern of the as prepared HAP calcined at 400°C for 3 h was shown in the Figure 2. After calcination, the powder form confirms the crystallinity structure of Ca10(PO4)6(OH)2 [HAP], and it is well fitted to hexagonal crystal structure [21].
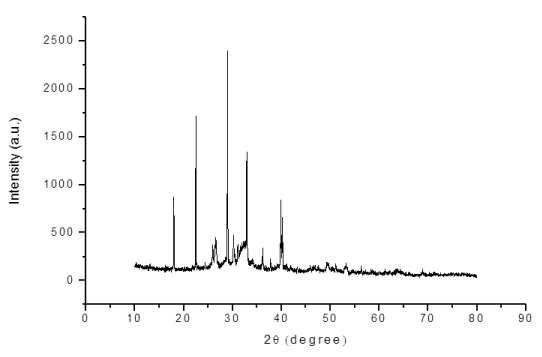
Figure 2. XRD of synthesised Hap
Energy dispersive X ray Fluorescence spectroscopy(EDXRF): To determine the composition of chemically synthesized HAP, energy dispersive spectroscopy study (EDS) [EDXRF, Panalytical Epsilon 5, Netherlands] was conducted and it is depicted in (Figure 3) (below). The EDS result showed that the synthesized HAP are composed of Ca, P and O only. There is no other peaks related to any impurity as per detection limit of EDS and so it is confirmed that the synthesized product is pure HAP composed of Ca, P and O. In XRF semiquantitative analysis Ca/P molar ratio is about 1.66 is observed and it is near to the theoretical value of 1.66, which support the structure of Hydroxyapatite.
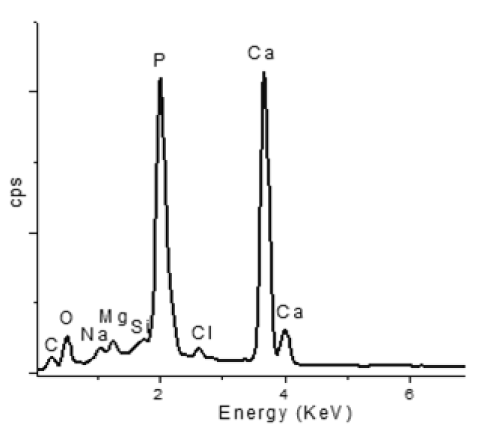
Figure 3. Determination of the chemical species present in the samples by elemental analysis using energy dispersion spectroscopy(EDS)
Batch adsorption studies
Effect of contact time: It is observed from Figure 4 that with increasing the contact time at particular temperature de-fluoridation efficiency increases. As the contact time increases, more the number of fluoride ions attached on the adsorbent surface. Chemically the accumulation of fluoride ions on adsorbent surface increases because of attraction force which results increase the percent removal of fluoride in solution.
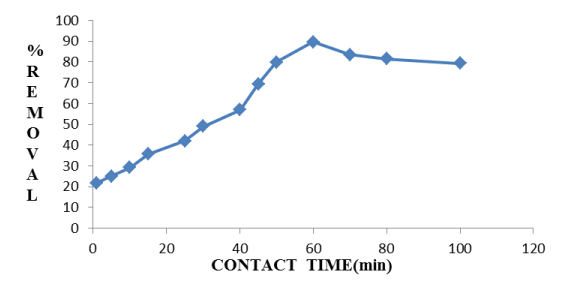
Figure 4. Effect of Contact time on de-fluoridation by Hap
Effect of adsorbent dose
Within the experimental range of adsorbent dose in between 0.1-2g/100mL percent removal of fluoride firstly increases, then decreases. The adsorbent dose in the range of 0.1-0.75g/100mL, de-fluoridation efficiency increases because of the number of ions increases on the adsorbent surface due to the attraction force of adsorbate ions with the adsorbent adsorbent dose higher than 0.75g/100mL, shows decrease in removal on the adsorbent surface because surface of adsorbent is saturated by adsorbate ions, and so the repulsive force between fluoride ions and adsorbent surface occurs which is reflected in Figure 5.
Effect of temperature: It is illustrated in Figure 6 that with increasing temperature, the percent removal of fluoride first increases from 308K to 323K. After 323K, de-fluoridation efficiency decreases Following the chemisorption process, increasing the number of adsorbate ions(fluoride) accumulate on adsorbent surface, the attractive force in between fluoride ions and Hap increases. But as temperature increases beyond 323K, as charge density of fluoride ions increases, the repulsive force increases in between adsorbate and adsorbent surface and as a result, the de-fluoridation efficiency firstly increases, then decreases.
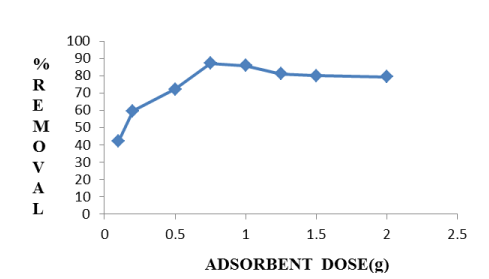
Figure 5. Effect of Adsorbent dose on de-fluoridation by Hap
Thermodynamics and kinetics study
Effect of adsorption isotherms: An adsorption isotherm is mathematically expressed by certain constants which elucidate the surface properties and affinity of an adsorbent towards solute. Experimentally obtained data from Langmuir and Freundlich models [22] (Figures 7A and 7B), it is observed that the Freundlich isotherm represents the experimental data better than Langmuir isotherm with initial fluoride concentration of 50 mg/L, 100 mL solution, pH of solution 0.3, adsorbent dose 0.75g/100mL, agitation time 60 min, temperature 323K. The Langmuir constant Qe is 4.3 mg g-1; b is 258.95 L mg-1 with a regression coefficient of 0.933, whereas in the Freundlich model Kf is 4.1(mg g−1)(L mg−1)1/n, n is 35.78(greater than 1) and the regression coefficient was 0.954. The experimentally obtained results of fluoride adsorption on Hap denotes monolayer adsorption. It is concluded that adsorption capacity increases from 303K to 323K which indicated that the chemisorption process is endothermic in nature.
Effect of adsorption kinetics and temperature: The linear plots of t/qt vs. t is shown in Figure 8. At 323K, the rate constant is 0.23 g mg−1 min−1 and the initial adsorption rate is 4.3 mg g– 1 min– 1. As a consequence from experimentally obtained results, it is proved that as temperature increased from 303 to 323K, the amount of fluoride adsorption increased. This phenomenon occurred due to raise in the mobility of fluoride ions with temperature and so, the adsorption capacity also increased with a rise in temperature.
From the pseudo second order rate constant k2 at different temperatures, the activation energy Ea is estimated using the Arrhenius energy equation (Eq 8). The slope calculated from Arrhenius equation is 39.89 kJ/mol. As the activation energy is greater than calculated value of Arrhenius energy.
From the batch experiment studies it is observed that as time increases, the efficiency of the reduction of fluoride increases as well as the adsorption capacity and after a certain time 89.6% removal of fluoride is obtained. From Figure 8, it is observed that t/Qt vs. t plot at different temperatures demonstrates the graphical plot is pseudo second order kinetics [23] at different temperatures. At 323K (Figure 8), t/Qt vs. t plot showing linear plot with regression coefficient 0.928. The linear plots of t/qt vs. t for different temperatures are shown in Figure 8. At a temperature of 323K, the rate constant is 0.2413 g mg– 1 min– 1 and the initial adsorption rate was 4.3 mg g–1min–1. This phenomenon indicates that Hap can be effectively used for fluoride adsorption in batch studies.
Thermodynamic parameters: From the experimental data following equation (Eq. 10,11) it represents that the negative value of ΔG0(-4874.82 kJ mol-1) increases with increasing in the temperature (up to 323K) which supports endothermic nature of the reaction due to consuming energy from the reaction system. The values of ΔH0 and, ΔS0 are estimated from the slopes and intercept of the plot ln Kc vs. (1/T) (Figure. not given) and the values are listed in Table 2.
It is observed that the negative value of ΔG0 at all temperatures represents that the fluoride adsorption reaction is spontaneous in nature [24]. In this case ΔG0 decreases up to 323K and after that it increases which indicated that the adsorption reaction is feasible up to 323K [25]. As a consequence the randomness in between fluoride ion and Hap surface in increased. As the reaction is endothermic in nature, it is expected that the uptake capacity of fluoride ions by Hap is increasing with temperature. But after 323K, the reverse reaction occur. Mathematically entropy of the reaction is estimated from the experimentally obtained data that is positive (15.222 Jmol−1K−1). So it is explained that as temperature is increased above 323K, the desorption occur on the Hap surface which results the concentration of fluoride in solution in increased in small amount in solution.
Table 2. Thermodynamic parameters for the adsorption of fluoride onto Hap
Serial No. |
T,K |
ΔG0, kJ mol-1 |
ΔH0, kJ mol-1 |
ΔS0,J mol−1 K−1 |
1 |
308 |
-10.24 |
-4654.4 |
15.222 |
2 |
313 |
-354.45 |
3 |
318 |
-1697.8 |
4 |
323 |
-4874.8 |
5 |
328 |
-2093.22 |
Estimation of response surface for maximum fluoride removal: The results of the 20 experiments performed as per CCD analysis are in Table 3. A maximum fluoride removal is obtained 89.65% at pH 0.3, at 323K and 0.75 g of adsorbent.
It is observed that B, C, AB, C2 are significant model terms. The F-value (16.34) with a low probability value (P) depicted high significance for the regression model. There is only 0.34% chance that an F-value this large could occur due to noise. Values of "Probability> F" less than 0.0500 indicate model terms are significant.
Table 3. Central composite design (CCD) used for optimizing three independent variables along with the obtained response
Serial No. |
A:Adsorbent dose(g) |
B:pH |
C:Temperature
(K) |
Removal of Fluoride
(R1%) |
1 |
0.75 |
4.5 |
323 |
78.4 |
2 |
0.5 |
7 |
313 |
68.5 |
3 |
0.33 |
4.5 |
323 |
76.4 |
4 |
0.5 |
2 |
333 |
75.3 |
5 |
0.5 |
7 |
333 |
50.1 |
6 |
0.5 |
7 |
313 |
68.5 |
7 |
0.5 |
2 |
313 |
88.4 |
8 |
0.75 |
4.5 |
339.82 |
58.3 |
9 |
0.75 |
4.5 |
323 |
78.4 |
10 |
0.75 |
0.3 |
323 |
89.6 |
11 |
0.75 |
4.5 |
306.18 |
75.3 |
12 |
0.75 |
8.7 |
323 |
71.1 |
13 |
1 |
2 |
333 |
66.3 |
14 |
1 |
2 |
313 |
71.3 |
15 |
1 |
7 |
313 |
84.6 |
16 |
1 |
7 |
333 |
73.5 |
17 |
1.17 |
4.5 |
323 |
73.9 |
18 |
0.75 |
4.5 |
323 |
78.4 |
19 |
0.5 |
7 |
313 |
68.5 |
20 |
0.75 |
4.5 |
50 |
78.4 |
|
|
|
|
|
|
|
In this case response surface quadratic model shows that the interaction effects of adsorbent dose, pH and temperature. In order to study the interaction among the different independent variables and their corresponding effect on the response, contour plots are drawn (Figures 10-12). A contour plot is a graphical representation of a three dimensional response surface as a function of two independent variables, keeping all other variables constant.
The response variable which is expressed as a function of independent variables defined in multiple regression model, developed by the software is expressed in the form of different numerical factors in equation (12) given below:
2021 Copyright OAT. All rights reserv
Removal % of fluoride (R1)=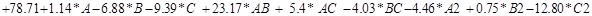
…………………………………… (12)
The goodness of fit of the model is checked by the correlation coefficient (R2) between the experimental and model predicted values of the response variable (Figure 9). Statistically R2 value of 0.9671 indicates that the model is statistically significant. The predicted correlation coefficient (pred. R2 0.8995) also shows good agreement with the adjusted correlation coefficient (adj. R20.9079). It indicates reliability of the data obtained by performing 20 experiments. Overall, the applicability of the model is used to predict the percentage removal of fluoride in solution within the limits of the experimental factors.
Interaction effect of process variables
Effect of variation in pH and adsorbent dose: The contour plot of Figure 10 demonstrated the interaction effects of the independent variables (pH and adsorbent dose) in the above response. According to the contour plot of Figure 10, de-fluoridation efficiency is increased as the adsorbent dose increased but decreases with the solution pH. The maximal removal efficiency of 89.6% is achieved at initial pH of 0.3 and adsorbent dose 0.75 g, while the other process variables are constant at the middle value.
Effect of variation in temperature and adsorbent dose: The effect of different temperature and adsorbent dose are required to remediate fluoride in solution using Hap. It is illustrated in the contour plot as shown in Figure 11. It is evident from Figure 11 that both the independent process variables had a strong effect on the % fluoride adsorption process. From this contour plot, a maximal removal efficiency of 89.6% is obtained at 323K and 0.75 g of Hap, while the other variable is set at the middle value. As the temperature increased in between 303-323K, the fluoride uptake capacity increased at particular contact time which indicated that at higher temperature with higher adsorbent dose, due to strong attraction force bound fluoride ions on the HAP surfaces which adsorbed and as a result % removal efficiency increased.
Effect of variation in pH and temperature: The combined effect of initial solution pH and temperature for adsorption on fluoride removal is depicted in the contour plot of Figure 12. It is observed that percentage of fluoride removal increased with increasing the temperature between 303K to 323K but increase not properly with initial solution pH increased. So it is explained that higher values of fluoride removal may be obtained by increase in temperature but decrease in initial solution pH. As pH increased, the % removal of fluoride decreased which supported the repulsion between fluoride ion and adsorbent at low pH. As pH of the solution increased, the charge density of adsorbent surface is decreased and as a result of electrostatic repulsion of the fluoride increased. From this contour plot, a maximal removal efficiency of 89.6% is achieved at an initial solution pH of 0.3, at 323K and 60 min of time.
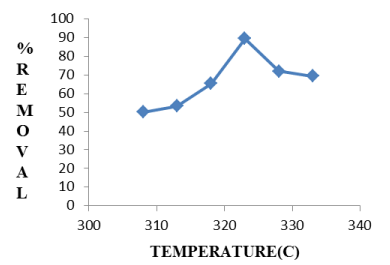
Figure 6. Effect of temperature on de-fluoridation by Hap
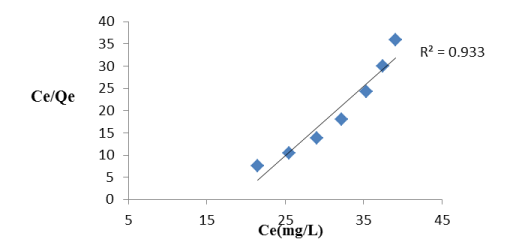
Figure7(A). Langmuir Isotherm plot of de-fluoridation by Hap

Figure7(B). Frendlich Isotherm plot of de-fluoridation by Hap
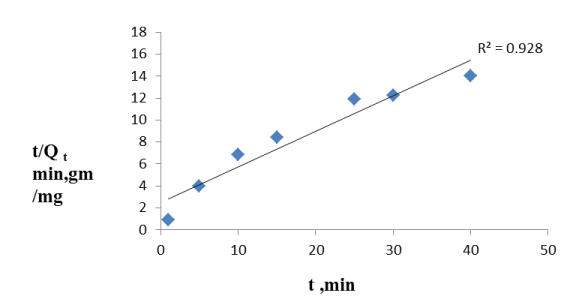
Figure 8. Linear Plot of t/qt vs t at 323 K
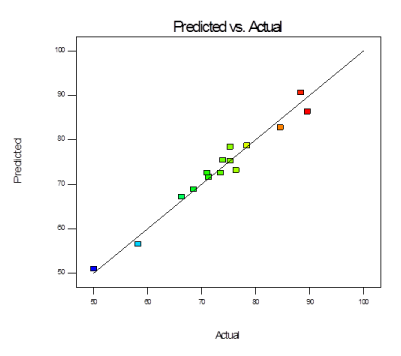
Figure 9. Graph showing predicted removal % Vs actual removal% of fluoride by adsorption
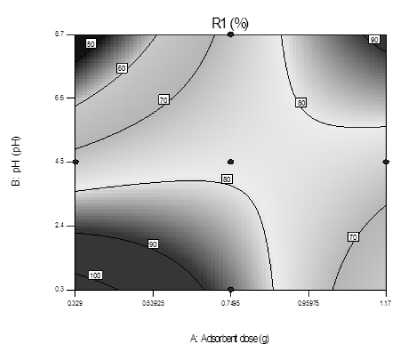
Figure 10. Contour plot showing interaction effect of adsorbent dose and pH

Figure 11. Contour plot showing interaction effect of temperature and adsorbent dose
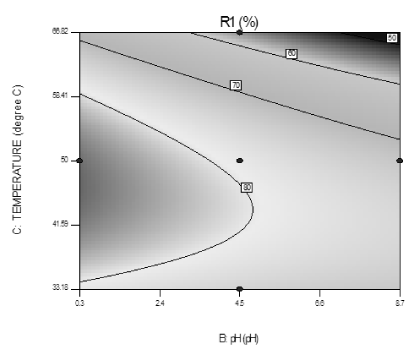
Figure 12. Contour plot showing interaction effect of pH and temperature
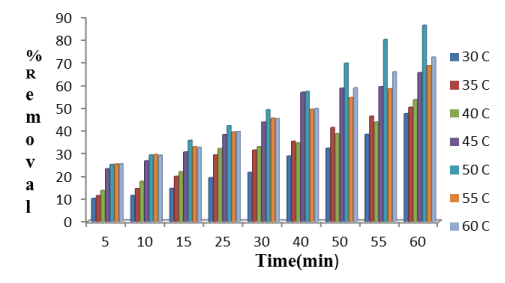
Figure 13. Plot showing percent removal of fluoride by Hap in batch studies at different temperature with respect to time
Confirmational study
To support the optimized data given by numerical modeling confirmatory experiments are conducted with the parameters as suggested by the model (adsorbent dose 0.75 g; pH 0.3; temperature 323K; contact time 60 minutes). These are found to be optimum for maximum percent fluoride removal. The corresponding removal efficiency in optimum conditions is found 89.6%.
Conclusion
The present study was conducted with the aim of fluoride adsorption process onto synthesized hydroxyapatite and to investigate the influence of various process parameters on fluoride removal using response surface methodology. The fluoride removal efficiency was significantly affected by the initial solution pH, contact time, adsorbent dose. The level of the three variables, initial solution pH 0.3, contact time 45 min, adsorbent dose 0.75 g were found to be optimum for maximum fluoride removal. The corresponding removal efficiency in optimum conditions was found to be 89.6%. Besides, it is proved that the adsorption equilibrium data are well fitted the Langmuir adsorption model at different temperatures. Also, the obtained experimental results are well fitted with pseudo –second order kinetic model. From the thermodynamic studies, it is proved that the nature of the adsorption process is spontaneous and the reaction mechanism is chemisorption in nature. As Hap is cost effective, so this may be an effective material for the treatment of wastewater treatment plant. Additionally, as this material is synthesized by precipitation method, so it can be used as an most effective adsorbent for the removal of fluoride ion from solution.
Acknowledgment
This study was supported by Chemical Engineering Department, Jadavpur University, Kolkata, India and West Bengal Pollution Control Board, India. Authors are thankful for their support and service.
References
- Agarwal M, Rai K, Shrivastav R, Dass S (2003) Defluoridation of water using amended clay. J Cleaner Produc 11: 439–444.
- Alkan E, Kir E, O¨ ksu¨ z L (2008) Plasma modification of the anion-exchange membrane and its influence on fluoride removal from water. Sep Purif Technol 61: 455–460.
- Abe I, Iwasaki S, Tokimoto T, Kawasaki N, Nakamura T, et al. (2004) Adsorption of fluoride ions onto carbonaceous materials. J. Colloid Interface Sci 275: 35–39. [Crossref]
- Annouar S, Mountadar M, Soufiane A, Elmidaoui A, Sahli MA, et al. (2004) Defluoridation of underground water by adsorption on the chitosan and by electrodialysis. Desalination 165: 437–438.
- Joschek S, Nies B, Krotz R, Goepferich A (2000) Chemical and physicochemical characterization of porous hydroxyapatite ceramics made of natural bone. Biomaterials 21: 1645–1658. [Crossref]
- Apambire WB, Boyle DR, Michel FA (1997) Geochemistry, genesis and health implications of fluoriferous groundwater in the upper regions of Ghana. Environ Geol 33: 13–24.
- Biswas K, Saha S, Ghosh UC( 2007) adsorption of fluoride from aqueous solution by a synthetic iron(III)–aluminum(III) mixed oxide. Ind Eng Chem Res 46: 5346–5356.
- Bjorvatn K, Bardsen A, Tekle Haimanot R (1997) Defluoridation of drinking water by use of clay/soil. In: 2nd Int. Workshop on fluorosis and defluoridation of water. Publ Int Soc Fluoride Res: 100–105.
- Bower CA, Hatcher JT (1967) Adsorption of fluoride by soils and minerals. J Soil Sci 3:151–154.
- Chaturvedi AK, Pathak KC, Singh VN (1988) Fluoride removal from water by adsorption on China clay. Appl Clay Sci 3: 337–346.
- Chaturvedi AK, Yadava KP, Pathak KC, Singh VN (1990) Defluoridation of water by adsorption on fly ash. Water Air and Soil Pollut 49: 51–60.
- Dahi E, Mtalo F, Njau B, Bregnhj H (1996) Defluoridation Using the Nalgonda Technique in Tanzania, 22nd Water, Engineering and Development Centre (WEDC) Conference, New Delhi, India.
- Das DP, Das J, Parida KM (2003) Physicochemical characterization and adsorption behavior of calcined Zn/Al hydrotalcite-like compound (HTlc) towards removal of fluoride from aqueous solution. J Colloid Interface Sci 261: 213–220.[Crossref]
- Fan X, Parker DJ, Smith MD (2003) Adsorption kinetics of fluoride on low cost materials. Water Res 37: 4929–4937. [Crossref]
- Tripathy SS, Srivastava SB, Bersillon JL, Gopal K(2004 Removal of fluoride from drinking water by using low cost adsorbents, in: Proceedings of the 9th FECS Conference and 2nd SFC Meeting on Chemistry and the Environment, Bordeaux, France, 352.
- Ghorai S, Pant KK (2005) Equilibrium, kinetics and breakthrough studies for adsorption of fluoride on activated alumina. Sep Purif Technol 42: 265–271.
- Han J, Song H, Saito F, Lee B (2006) Synthesis of high purity nano-sized hydroxyapatite powder by microwave-hydrothermal method Mater Chem Phys 99: 235–239.
- Tas AC (2000) Synthesis of biomimetic Ca-hydroxyapatite powders at 37°C in synthetic body fluids. Biomaterials 2: 1429–1438. [Crossref]
- Jain M, Garg VK, Kadrivelu K (2011) Investigation of Cr(VI) adsorption onto chemically treated Helianthus annus: Optimization using response surface methodology. Bioresour Technol 102: 600–605.
- Bas D, Boyaci IH (2007) Modeling and optimization II: Comparison of estimation capabilities of response sur-face methodology with artificial neural networks in a biochemical reaction. Journal of Food Engineering 78: 846-854.
- Koutsopoulos S (2002) Synthesis and characterization of hydroxyapatite crystals: A review study on the analytical methods. Journal of Biomedical Materials Research Part A, 62: 600-612. [Crossref]
- Wong YC, Szeto YS, Cheung WS, McKay G (2004) Adsorption of acid dyes on chitosan - equilibrium isotherm analyses. Process Biochem 39: 693–702.
- Sandrine B, Ange N, Didier BA, Eric C, Patrick S (2007) Removal of aqueous lead ions by hydroxyapatites: equilibria and kinetic processes. J Hazard Mater139: 443–446.[Crossref]
- Dotto GL, Pinto LAA (2011) Adsorption of food dyes onto chitosan: optimization process and kinetic. Carbohydr Polym 84: 231–238. [Crossref]
- Anirudhan TS, Radhakrishnan PG (2008) Thermodynamics and kinetics of adsorption of Cu (II) from Aqueous Solutions onto a new cation exchanger derived from tamarind fruit shell. J Chem Thermodyn 40: 702.














