Abstract
Bipolar quantum agent (BQA), bipolar quantum geometry (BQG) and bipolar dynamic logic (BDL) are introduced based on bipolar complementarity – a logical extension to Niels Bohr’s particle-wave YinYang duality principle. Complete geometrical background independence is proposed and BQG is proven completely background independent which leads to the notion of bipolar quantum superposition – an equilibrium-based logical approach to superposition. It is shown that the logical linearity of BDL can be unified with the physical nonlinearity of bipolar dynamic equilibrium. It is proven that a single polarized photon as a BQA can be logically channeled through the three polarizers in Dirac’s experiment with BDL regardless of quantum uncertainty. It is illustrated that BQG, BDL and bipolar probability adds analytical power to quantum mechanics. It is concluded that bipolar quantum superposition demystifies Schrödinger's cat paradox from a weird quantum phenomenon to a logically comprehendible YinYang bipolar dynamic equilibrium interpretation of quantum superposition and leads to an analytical paradigm of quantum mechanics and quantum biology as presented in Part II of this work.
Key words
Dirac 3-polaizer experiment, single polarized photon, bipolar quantum agent, bipolar quantum geometry, bipolar quantum superposition, logical linearity and physical nonlinearity, bipolar probability
Introduction
Optics –a field of physics focusing on the study of light – is also central to many areas of biological and life sciences, including vision, ecology, botany, animal behavior, neurobiology, and biology at the system, cellular, molecular, and quantum levels. The inner workings of photosynthesis, however, has not been fully understood in quantum biology [cf. 1]. The role of quantum agents and quantum intelligence [2,3] has not been investigated in swarm intelligence and carcinogenesis [4,5]. Despite the great success of quantum mechanics, the quantum nature of fractals [6] so far remains largely unknown. How a single photon moves around is still a logical mystery [7,8] (Figure 1). Quantum computing has been troubled with quantum decoherence and/or collapse associated with the “measurement” problem.
In his text book [7], Paul Dirac introduced the concepts of quantum superposition and indeterminacy using polarized photons in a 3-polarizer experiment (Figures 1(a-d) and Eq. 1). As Dirac stated [7, p11]: “There remains an overall criticism that one may make to the whole scheme, namely, that in departing from the determinacy of the classical theory a great complication is introduced into the description of Nature, which is a highly undesirable feature. This complication is undeniable, but it is offset by a great simplification, provided by the general principle of superposition of states, which we shall now go on to consider.”Albert Einstein commented on Dirac’s experiment [8]: "Dirac, to whom, in my opinion, we owe the most perfect exposition, logically, of this theory, rightly points out that it would probably be difficult, for example, to give a theoretical description of a photon such as would give enough information to enable one to decide whether it will pass a polarizer placed (obliquely) in its way or not."

Figure 1. Dirac three polarizer experiment and quantum superposition: (a) Two vertical (or horizontal) polarizers; (b) A vertical polarizer and a horizontal one; (c) A diagonal polarizer inserted between a vertical and a horizontal polarizer; (d) Quantum superposition; (e) Fractal-like photon superposition after a single slit (http://creativecommons.org/licenses/by/3.0/)

Despite the theoretical significance, Dirac’s examples suggest a very simple and inexpensive experiment to demonstrate quantum superposition of polarized photons. Such an experiment is usually performed in high school physics labs. The experiment tells us:
- Light gets through polarizers (filters) A and B if both are aligned vertically or horizontally (Figure 1a);
- If polarizer A remains in vertical polarization and polarizer B is rotated 90° to horizontal polarization, no light gets through (Figure 1b);
- Light partially gets through the intersection of Polarizer C with polarizer A and polarizer B if C is turned along the diagonal 45° and slipped between A (in the rear) and B (in front) (Figure 1c).
According to Dirac, with complex number coefficients that represent "probability amplitudes", the diagonally polarized photon can be represented as a superposition of vertical v and horizontal h states (Figure 1(d), Eq. 1). Einstein and Schrödinger later attacked the idea of superposition by arguing that it would apply to macroscopic objects like a cat being alive and dead. This quantum phenomenon has been referred to as Schrödinger's Cat paradox. After many decades, it is still an unknown whether there is a geometrical and logical system that can be used to reason on the paradoxical phenomenon qualitatively such that the weird quantum mechanical nature of polarized photons can be revealed analytically.
This paper attempts to provide an answer to the above fundamental question. It is organized into five sections. Following this introduction an axiomatic framework is presented in Section 2 including: (1) the principle of YinYang bipolar complementarity – a logical extension of Niels Bohr’s wave-particle YinYang duality, (2) the concept of equilibrium-based bipolar quantum agents – an ontological basis for YinYang bipolar dynamic logic (BDL) [2], and (3) bipolar quantum geometry (BQG) – a completely background independent approach to geometry that supports both reductionism and emergence through bipolar interaction. The logical linearity and physical nonlinearity of BDL and bipolar quantum linear algebra (BQLA) [2] are analyzed. With BQG and BDL, a nonlinear bipolar dynamic logical exposition of Dirac 3-polarizer experiment is presented in Section 3. It is shown that a single photon as a nonlinear dynamic BQA can be logically channeled through the three polarizers. Bipolar probabilistic reasoning is introduced in Section 4 and compared with the probability amplitude model using complex number coefficients. It is shown that the essence of quantum superposition is bipolar dynamic equilibrium. Section 5 draws a few conclusions.
Axiomatic formulation
From wave-particle duality to bipolar complementarity
Niels Bohr was the first to bring YinYang into quantum theory for his wave-particle duality principle. When Bohr was awarded the Order of the Elephant by the Danish government, he designed his own coat of arms (Figure 2a) which featured in the center a YinYang logo and the Latin motto contraria sunt complementa or “opposites are complementary” in English.
It is observed, however, that particle and wave are not direct opposites. While Bohr recognized wave-particle complementarity, he stopped short of identifying the essence of Yin Yang bipolar coexistence and bipolar complementarity (Figure 2b).
Theoretically, if bipolar dynamic equilibrium of negative-positive energies and/or input-output information is the most fundamental form of equilibrium, any multidimensional model in spacetime geometry is less fundamental. A Yin Yang bipolar complementarity principle is, therefore, imperative for a bipolar equilibrium-based logical interpretation of the quantum world.
YinYang bipolar complementarity principle: Action-reaction, particle-antiparticle, input-output, negative-positive, or the Yin and the Yang of Nature in general constitute the direct opposites (Figure 2(b)), form the most fundamental complementarity, and provide the source of causality for being and changes. On the other hand, without bipolarity, any complementarity is less fundamental due to the missing “opposites” (Figures 2(c-d)) (extended from [2]).
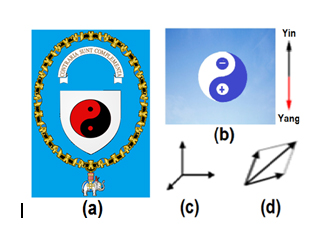
Figure 2. (a) Bohr’s Coat of Arms (Creative Commons file by GJo, 3/8/2010, File:Royal Coat of Arms of Denmark.svg + File:yinyang.svg); (b) Fundamental bipolar complementarity; (c)-(d) Non-fundamental complementarities
According to the bipolar complementarity principle, man-woman, space-time, particle-wave, truth-falsity, mind-matter, and imaginary-real complementarities are not exactly bipolar opposites and, thus, less fundamental. For instance, while particle-wave and space-time do not interact with each other as bipolar opposites, they can be posited the result of particle-antiparticle bipolar interaction. This could be the reason why Bohr asserted that a causal description of a quantum process cannot be attained and quantum mechanics has to content itself with wave-particle complementary descriptions [9]. It can be posited that, due to this limitation, Bohr’s complementarity principle so far has not evolved to a general purpose logical system for quantum mechanics and a logical exposition of quantum superposition.
A background independent approach to geometry
Based on the YinYang bipolar complementarity principle, we have:
Definition 1: A bipolar dynamic equilibrium is a process of bipolar interaction and state change among bipolar equilibrium, non-equilibrium, and eternal equilibrium states.
Definition 2: A bipolar quantum agent (BQA) is a bipolar dynamic equilibrium. A global bipolar dynamic equilibrium may subsume local ones and a non-elementary BQA may consist of elementary BQAs. (Adapted from [2,3])
Based on Definition 1, any elementary quantum particle, antiparticle, or dipole as a bipolar dynamic equilibrium is qualified to be an elementary BQA at the subatomic level; all agents are qualified to be BQAs at an elementary or non-elementary level because any agent consists of a set of quantum particles. Thus, the concept of BQA makes it possible to investigate into the equilibrium-based quantum nature of agents and intelligence [2,3].
Axiom 1: If an elementary particle or BQA is in a non-equilibrium negative state that can be characterized with the bipolar value (-1,0), its antiparticle must be a BQA in another non-equilibrium state that can be characterized with the bipolar value (0,+1) and the two in a pair without annihilation must be a BQA in an equilibrium state which can be characterized with the bipolar value (-1,+1). The non-existence after decay or annihilation of the particle-antiparticle pair can be characterized with an eternal equilibrium state with the bipolar value (0,0).
Axiom 2: If an elementary particle is its own antiparticle, the BQA must have distinct states that can be characterized as negative (-1,0), positive (0,+1), bipolar equilibrium (-1,+1) and eternal equilibrium (0,0), respectively.
Figure 3 shows different bipolar interactions.
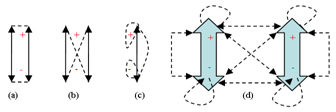
Figure 3. Bipolar interaction: (a) Non-reciprocal bipolar interaction; (b) Reciprocal bipolar interaction; (c) Bipolar oscillation; (d) Bipolar entanglement
Based on Definitions 1-2 and axioms 1-2, we have
Axiom 3: A BQA as a bipolar dynamic equilibrium can emerge from the Yin and the Yang of Nature and can submerge to the Yin and the Yang.
The above definitions and axioms lead to the extension of YinYang bipolar geometry [2] to bipolar quantum geometry.
Definition 3: Bipolar quantum geometry (BQG) has three shape-free and quadrant-irrelevant dimensions: the Yin and the Yang dimensions are the two reciprocal and interdependent bipolar opposites from which a third dimension – bipolar dynamic equilibrium – can emerge as a bipolar quantum superposition of the Yin and Yang dimensions.
While background independent geometry is advocated for quantum gravity (cf. [10]), it stopped short of specifying a minimum set of necessary and sufficient conditions for complete background independence. Without such a set of conditions, a unique logical foundation for quantum gravity cannot be developed and a logical exposition of Dirac 3-polarizer experiment has been impossible. For instance, until this day, the Wikipedia definition of a background independent geometry requires the unnecessary condition of being coordinate-free but does not require the imperative condition of supporting both reductionism and emergence. Such unnecessary and/or insufficient conditions have inhibited the emergence of a truly background independent geometry and a new formal logical foundation for quantum gravity. As a result, the quest for quantum gravity has so far failed to find a definitive battleground and quantum superposition still find no logical definition.
Definition 4: A geometry with complete background independence must satisfy the minimum set of conditions: (1) it is shape-free, quadrant irrelevant and spacetime transcendent; (2) it supports both reductionism and emergence; (3) it is ubiquitous.
Theorem 1: BQG satisfies the conditions of complete background independence.
Proof: (1) Since the Yin and the Yang of Nature are independent of the shape of spacetime and the value of fields within spacetime, BQG is shape-free, quadrant irrelevant and spacetime transcendent. (2) Since the Yin and the Yang of a system or subsystem can form, respectively, global or local bipolar dynamic equilibrium – a unitary truth object, BQG can support equilibrium-based reductionism. On the other hand, since BQA as a bipolar dynamic equilibrium can emerge, BQG supports emergence as well. (3) BQG is ubiquitous because the Yin and the Yang of Nature is ubiquitous.
Figures 4 (a-c) shows a sketch of BQGas an extension of YinYang bipolar geometry [2] with a comparison to Dirac’s quantum superposition in Figure 4(d) [7].
(a) (b) (c)(d)
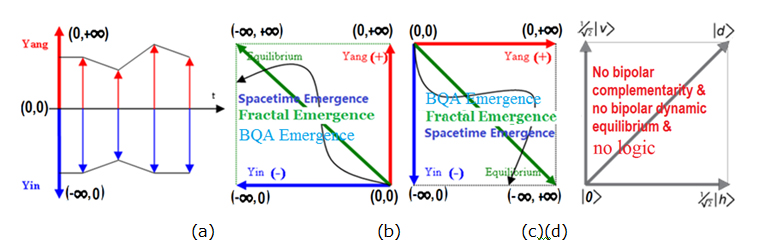
Figure 4. A comparison: (a) Magnitude model of BQG;(b)-(c) Background independent property of BQG; (d) Dirac’s quantum superposition.
Since the Yin and the Yang are two reciprocal and interdependent opposites of a dynamic equilibrium that are completely background independent and ubiquitous, BQG is fundamentally different from Euclidian, Hilbert, and spacetime geometries. With complete background independence, BQG provides a geometrical basis for bipolar interaction and bipolar quantum superposition and bipolar quantum entanglement that transcends spacetime [2,11-14]. With the shape-free and quadrant-irrelevant properties, BQG can host BQAs anywhere in any amount of bipolar energy/information for investigating into the quantum nature of shaped objects or fractals [6]. Shapes and quadrants can be added where observer is involved and background dependent information is needed. Thus, BQG can subsume other geometries and can be used to reason on space and time as well.
With BQG, bipolar quantum superposition can be deemed an equilibrium-based extension of Dirac’s quantum mechanical interpretation of quantum superposition. A comparison of Figures 4(a-c) with Figure 4(d) reveals that, while the quantum mechanical interpretation as a background-dependent approach within Hilbert space does not account for Nature’s bipolarity, the YinYang bipolar interpretation claims that any BQA as a bipolar dynamic equilibrium can emerge and submerge from bipolar quantum interaction.
Bipolar dynamic logic (BDL) and bipolar quantum linear algebra (BQLA)
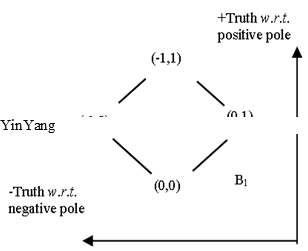
BQA and BQG provide an ontological and geometrical basis for an equilibrium-based mathematical abstraction of both reductionism and emergence. The equilibrium-based mathematical abstraction have led to bipolar dynamic logic (BDL), bipolar dynamic fuzzy logic (BDFL) and bipolar quantum linear algebra (BQLA) [2,12,13,15-18]. BDL (see Appendix) is a bipolar dynamic generalization of Boolean logic (BL) [19]. It is defined on the quantum lattice or causal set B1={-1,0}×{0,+1} = {(0,0), (-1,0), (0,+1), (-1,+1)}, where (0,0) characterizes an eternal equilibrium state; (-1,0) characterizes a non-equilibrium (negative) state; (0,+1) characterizes another non-equilibrium (positive) state; (-1,+1) characterizes a bipolar equilibrium state. BDFL can be deemed a real-valued extension of BDL on one hand or a bipolar dynamic generalization of fuzzy logic (FL) [20] for bipolar probabilistic reasoning on the other hand. BQLA can be deemed an algebraic extension of BDL and BDFL on one hand or a bipolar dynamic generalization of linear algebra (LA) on the other hand. A comparison of the generalizations with the generalized reveals that
- BL is truth-based without physical semantics and BDL is equilibrium-based with both logical and physical semantics. BDL generalizes BL from the truth-based domain or Boolean lattice L={0,1} to the equilibrium-based domain or quantum lattice B1={-1,0}×{0,+1}. BL is not a causal logic. BDL is a formal causal logic (see appendix).
- BDFL is a bipolar dynamic generalization of FL from the truth-based domain or fuzzy lattice LF=[0,1] to the equilibrium-based domain or quantum lattice BF=[-1,0]×[0,+1].
- BQLA is a bipolar dynamic generalization of linear algebra (LA) from the truth-based domain or lattice L∞=[-∞,+∞] to the equilibrium-based domain or quantum lattice B∞=[-∞,0]×[0,+ ∞].
- Without bipolarity BL, FL and LA are inadequate for the direct representation of a BQA with equilibrium and non-equilibrium states.
- Without a shred of dynamics, truth-values cannot form a causal set like B1, BF and B∞.
- BDL, BDFL and BQLA subsume BL, FL and LA because any being or truth in spacetime must exist in a bipolar dynamic equilibrium of input-output information or negative-positive energies.
- BL, FL and LA can be used together with BDL, BDFL and BQLA as long as equilibrium or non-equilibrium conditions are not violated.
With BDL, quantum superposition in Dirac’s bra-ket notation as shown in Eq. 1 can be simplified to Eq. 2(a) in bipolar logical form; with BQLA Eq. 1 can be simplified to Eq. 2(b) in bipolar algebraic form. Eqs. 2(c) and 2(d) relate bipolar variable to a vector and its amplitude. The bipolar simplification makes it possible to avoid complex number coefficients. Since BQG is background independent, vertical (v) and horizontal (h) as two direct opposites in a bipolar dynamic equilibrium can either be negative or positive, respectively. Without bipolarity, however, Dirac’s quantum superposition principle does not account for bipolar complementarity, does not support BQA emergence, and stopped short of evolving to a logical system. BQG and BDL, on the other hand, provides a geometrical and logical basis for an analytical paradigm of quantum mechanics.

Unification of logical linearity and physical nonlinearity
All agents are input/output (I/O) systems that can be classified as linear or nonlinear. If we apply input x to a dynamic system and obtain output y, scaling input x may give a scaled y such as the input ax leads to ay, where a is a scalar. When this property is true, we say that the I/O system is a linear system. Otherwise, it is nonlinear.
Similarly, a logic is said a linear logic if it satisfies the distributive law such as A˄(BÚC)= (A˄B)Ú(A˄C) where A, B or C assumes a truth value 0 or 1 which can be deemed a scalar for false or true, respectively. Thus, Boolean logic can be said a linear logic. A generalization of Boolean logic and intuitionistic logic can be achieved by a linear logic (Girard, 1987).
Logical linearity and physical nonlinearity can be deemed a duality. It is unclear, however, how to unify logical linearity and physical nonlinearity for nonlinear dynamic logical reasoning of quantum superposition. Is there a dynamic logic that is logically linear but physically nonlinear?
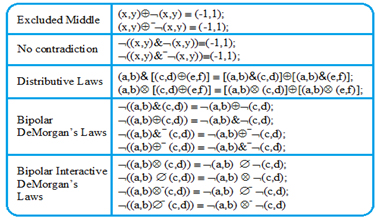
BDL, BDFL and BQLA are characterized [2] as equilibrium-based generalizations of BL [19], FL [20] and LA, respectively. The generalizations are bipolar dynamic in nature due to bipolar interaction. Whether they are linear or nonlinear is a matter of debate. While BDL was said a nonlinear bipolar dynamic generalization of BL [2,11-14], it can be argued that it is nothing more than a hyperspatial linear extension of BL. This argument is a strong one because bipolar distributivity of Ä and Å as well as & and Å, the very definition of linearity, is indeed maintained with BDL (see Appendix Table 2).
A further examination, however, reveals that, due to equilibrium-based bipolar dynamic interaction, BDL presents a unification of logical and physical systems. Since all beings must exist in certain bipolar dynamic equilibrium of input-output (I/O) or negative-positive energies/information, the bipolar operators can characterize different bipolar dynamic interactions and can change an equilibrium state to a non-equilibrium state with nonlinear bipolar dynamic behaviors. For instance, a(input, output) or a(-pole, +pole) is a linear scaling if a is a scalar; (-1,0) &-(-1,+1) = (0,+1) is logically linear but physically non-linear because a bipolar variable is not a scalar and a bipolar operator does not scale. Thus, logically, the binary operators of BDL are linear or bilinear that provide a basis for the soundness of the logic; physically it has nonlinear dynamics embedded and is inherently nonlinear. This is fundamentally different from truth-based linear or bilinear systems [21] which do not assume equilibrium-based physical semantics.
It may be further argued that linearity is determined by mathematical property but not physical property of an application. This argument cannot hold because it tries to force the linear or nonlinear property of truth-based mathematical abstraction upon an equilibrium-based one. Although equilibrium-based modeling used to be application, now BDL has been proven an equilibrium-based bipolar generalization of Boolean logic and it can be said logically linear but physically nonlinear. Its logical linearity provides a basis for logical soundness; its inherent nonlinear bipolar dynamic physical property, on the other hand, qualifies it to be a general purpose logic for bipolar dynamic reasoning on quantum superposition and entanglement. As a matter of fact, if the Dao of Yin Yang is a holistic bipolar dynamic equilibrium system that subsumes the universe, Yin Yang BDL is supposed to unify logical linearity and physical nonlinearity. The unification makes nonlinear bipolar dynamic reasoning possible with logical soundness. On the other hand, it provides a logical basis for both reductionism and emergence in bipolar quantum geometry.
With the logical basis, BQLA borrows the forms of classical linear algebra but performs nonlinear bipolar dynamic operations in bipolar dynamic equilibrium domains. As a nonlinear bipolar dynamic generalization of LA, BQLA is to BDL as LA is to BL or BQLA is to LA as BDL is to BL.
A logical exposition of Dirac 3-polarizer experiment
Polarized photons can be deemed ubiquitous BQAs. Based on bipolar complementarity, BDL provides a chance for a photon to be logically channeled through the three polarizers in BQG (Figure 4).
Theorem 2. A single incoming polarized photon can be logically channeled through the three polarizers in Dirac’s experiment with BDL in BQG regardless of quantum uncertainty or probability.
Proof: Since photon is its own antiparticle, following Axioms 1 and 2 we make the background independent and quadrant irrelevant assumptions: (1) a vertically polarized photon state is a positive state (0,+1); (2) a horizontally polarized photon state is a negative state (-1,0); (3) a diagonally polarized photon state is a bipolar equilibrium state (-1,+1); (4) (0,0) stands for no light.
- Let vertical polarizers A and B be both in state (0,+1) or let two horizontal polarizers be both in state (-1,0), logically, we have A&B = (0,+1)&(0,+1) = (0,+1) or A&B = (-1,0) & (-1,0) = (-1,0), respectively. Light gets through A&B in both cases.
- Let vertical polarizer A be in state (0, +1) and horizontal polarizer B in state (-1, 0), A&B = (0,+1)&(-1,0) = (0,0). No light gets through A&B.
- Let diagonal polarizer C (45°) be in bipolar equilibrium state (-1,+1), the question is how a single photon can logically get through A, C and B if C is slipped between A and B.
Is there a bipolar conjunctive operator in BDL that allows a single photon to get through the three polarizers in Case (c)? The problem can be formulated as: What is the unknown operator * such that
(i) A* C & B =(0, +1)* (-1, +1) & (-1, 0) = (-1, 0) or
(ii) A* C & B =(-1, 0)* (-1, +1) & (0, +1) = (0, +1)?
If the Boolean operator & takes effect in the place of *, light can only get through the diagonal polarizer C but cannot get through B as we have:
A&C&B =(0,+1)&(-1,+1)&(-1,0) = (0,+1)&(-1,0) = (0,0); or (3a)
A&C&B =(-1,0)&(-1,+1)&(0,+1) = (-1,0)&(0,+1) = (0,0). (3b)
BDL does, however, have another conjunctive &- such that X&-Y=-(X&Y) [2]. Substitute * with &- we have:
A&-C&B =(0,+1)&-(-1,+1)&(-1,0) = (-1,0)&(-1,0) = (-1,0); or (3c)
A&-C&B =(-1,0)&-(-1,+1)&(0,+1) = (0,+1)&(0,+1) = (0,+1). (3d)
Eqs. 3(c-d) shows that an incoming single polarized photon (vertically or horizontally prepared, respectively) can be logically channeled through the three polarizers with equilibrium-based BDL regardless of inherent quantum uncertainty.
The operator &- in BDL was perhaps the most counter intuitive and least expected one to find a meaningful application. Now, not only is it applicable but also shows the clear physical semantics: It enables the diagonal polarizer C to act as an ± oscillating-conjunctive or a relay to channel an incoming polarized photon through the three polarizers.
On the other hand, the diagonal polarizer can be deemed a balancer that exhibits either & or &- functionality with bipolar probability to balance incoming vertically or horizontally polarized photons to a bipolar equilibrium state. Without bipolar complementarity and bipolar geometry, however, such illogical nonlinear bipolar dynamic causal property could not have been logically described with wave-particle duality in spacetime geometry.
Bipolar probability and bipolar quantum superposition
While Dirac tells us that “diagonally polarized photon can be represented as a superposition of vertical and horizontal states, with complex number coefficients that represent probability amplitudes," the nature of superposition has never been logically clarified. While a single photon is the focus in Theorem 2, we show in what follows that quantum superposition can be demystified as a bipolar dynamic equilibrium with bipolar probability.
Theorem 3: The nature of quantum superposition is bipolar dynamic equilibrium or bipolar quantum superposition.
2021 Copyright OAT. All rights reserv
Proof: Since Eqs. 3(c) and 3(d) are symmetrical cases, we consider Eq. 3(c) without losing generality as follows:
- If a photon comes through vertical polarizer A it must be in vertical (+) state with bipolar probability (-pa,+pa) = (0, +1)Î [-1, 0] × [0, +1];
- Assuming the vertically prepared photon has a sin2(45°) = ½ probability to enter the diagonal (45°) polarizer C without being blocked and absorbed as heat, following Theorem 2, ½ of the photons can get through C either in vertical(+) or horizontal(-) state depending on whether the & or the &- operator takes effect with probability = ½ for each that leads to the bipolar probability for a vertically prepared photon after A to get through C: (-pc,+pc) = 1/2 × (1/2,+1/2) = (-1/4, +1/4) ϵ [-1, 0] × [0, +1].
- If a photon that gets through C is in vertical(+) state, it cannot pass the horizontal polarizer B with probability to pass = 0; if a photon that gets through C is in horizontal (-) state, it will pass the horizontal polarizer B with probability to pass = 1; the two cases lead to the bipolar probability (-pb,+pb) = (-1,0);
Based on the above analysis, the bipolar probability for one of many vertically prepared photons to pass (A) &-(C) & (B) (Eq. 3(c)) is shown in Eq. 4(a) which can be simplified to unipolar form as shown in Eq. 4(b).
(-p, +p) = (-pa,+pa)&- (-pc,+pc)& (-pb,+pb)
= (0, +1) &- (-1/4, +1/4) & (-1, 0)
= (-1/4, 0) & (-1, 0) = (-1/4, 0). (4a)
p = 1 × 1/4 × 1 = 1/4. (4b)
Based on Dirac’s quantum superposition principle (Eq. 1), the probability for a vertically prepared photon to pass C is (1/Ö2)2 = ½ and the probability for a photon prepared by C to pass B is also (1/Ö2)2 = ½ where (1/Ö2)2 is a conversion from complex number coefficient to probability. Thus, the probability for a vertically prepared photon to pass A, B and C by the quantum mechanical interpretation is formulated in Eq. 4(c).
P = 1 × (1/Ö2)2 ×(1/Ö2)2 = (1/2)2 = 1/4. (4c)
A comparison of Eqs. 4(a-b) with 4(c) reveals that
- Both interpretations have the same final result probability p =1/4. The quantum mechanical interpretation is mathematical but not logical; the bipolar equilibrium-based interpretation is both logical and probabilistic in nature.
- While Dirac described light as a kind of superposition of a vertical state v and a horizontal state h in Eq. 1 in a way that cannot be conceived on classical ideas, the bipolar logical exposition is logically conceivable on a single polarized photon following Theorem 1.
- While a horizontal or vertical polarizer simply filters out photons that are not horizontal or vertical, respectively, a diagonal polarizer can behave as a bipolar balancer. Thus, polarizer C can switch half incoming photons from vertical state to horizontal state (or vice versa) and the half can be channeled through polarizer B.
- The vertically polarized photons (the Yang) and the horizontally polarized photons (the Yin) that get through the diagonal polarizer C form a bipolar dynamic equilibrium or bipolar superposition in diagonal orientation. The Yin and the Yang as well as their bipolar equilibrium are well-observed in experiments.
Remarkably, different interpretations of quantum mechanics all lead, in practice, to exactly the same answers and predictions regarding the observations. The bipolar dynamic equilibrium-based interpretation, however, leads to bipolar quantum superposition. The new interpretation fundamentally differs from the quantum mechanical interpretation with its bipolarity and logically definable causality vs. Hilbert space without bipolarity and logically definable causality. Thus, the new interpretation constitutes a deeper theory that is vindicated by the same answers and observations.
Figures 5 and 6 provide a geometrical comparison of the two different approaches to quantum superposition. In Figure 5 the area of a square converts complex number coefficients to the probability amplitude of a photon that can pass a polarizer. While complex numbers provide a powerful computational tool in Hilbert space, it makes quantum superposition mysterious without a unique logical system for equilibrium-based bipolar dynamic reasoning. Thus, the analytical power of the quantum mechanical interpretation of superposition is compromised by the complex number coefficients.
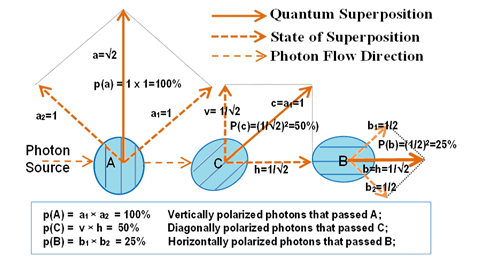
Figure 5. Quantum mechanical interpretation of quantum superposition without bipolarity and logically definable causality.

Figure 6. Equilibrium-based logical interpretation of quantum superposition with bipolar probability and logically definable causality in BQG
Figure 6 provides a picture for the equilibrium-based logical interpretation of quantum superposition. In the new interpretation, all quantum states are represented by bipolar scalar values of the Yin and the Yang in equilibrium or non-equilibrium. The bipolar scalar representation provides a basis for BDL, BDFL and BQLA for logical, probabilistic and algebraic reasoning and computation on quantum superposition.
For instance, the probability for a vertically prepared photon to pass the diagonal polarizer C as a square of a complex number coefficient is (1/Ö2)2= ½. But Figure 5 can be easily represented in Figure 6 by an equilibrium-based bipolar probability value (-1/4, +1/4). Evidently, we have |-1/4|+|1/4| = (1/Ö2)2=½. In general, the bipolar probability amplitude of a bipolar variable p = (p-, p+) can be defined as |p| = |p-| + |p+|. A scalar probability is much simpler and more meaningful than complex coefficients for analytical purposes. Thus, the bipolar equilibrium-based approach leads to an analytical paradigm of quantum superposition.
The comparison further confirms that YinYang bipolar complementarity is the most fundamental complementarity which may lead to the emergence of a bipolar quantum superposition. On the other hand, the real and imaginary dimensions in Hilbert space are not most fundamental because they do not support background independent bipolar interaction and emergence.
Conclusions
The principle of YinYang bipolar complementarity – a logical extension of Niels Bohr’s particle-wave duality – has been proposed; the concepts of bipolar quantum agents (BQAs), bipolar quantum geometry (BQG) and bipolar probability have been presented. Different from other approaches, the new geometry is equilibrium-based and completely background independent. Based on BQG and bipolar probability, quantum superposition has been logically revealed as a YinYang bipolar dynamic equilibrium which has led to the notion of bipolar quantum superposition.
To the authors’ knowledge bipolar quantum superposition is the first equilibrium-based logical interpretation of quantum mechanics. Since the logical exposition of Dirac 3-polarizer experiment has not been possible with other interpretations and the new interpretation has been shown in full conformity with existing well-known experimental observations, bipolar quantum superposition has been vindicated by the exposition and the observations. From now on, the longstanding weird phenomenon of quantum superposition can be deemed a logically definable and analytically comprehendible bipolar dynamic equilibrium.
While it has been true that different interpretations of quantum mechanics so far all lead, in practice, to exactly the same answers and predictions regarding the observations, the significance of this work is to position quantum mechanics on a formal geometrical and logical basis with definable causality. Without such a basis, Einstein refused to accept quantum mechanics as a complete theory [22] and famously called quantum entanglement “spooky action in a distance”. On the other hand, without such a basis, quantum fractality is so far largely mysterious and quantum biology has remained a research area in its infancy for decades.
It is expected that YinYang bipolar quantum geometry and superposition will serve as a geometrical and logical basis toward a complete theory of quantum mechanics and an analytical paradigm of quantum biology. While bipolar quantum superposition in Part I is limited to the generic case at the logical level, a scalable bipolar quantum cellular automaton interpretation of quantum mechanics and quantum biology with multidimensional bipolar quantum superposition and fractality is reported in Part II of this paper [23].
Acknowledgement
The authors acknowledge the editor and the anonymous reviewers of this and other journals for their critical and constructive comments on earlier versions of this paper.
References
- Ball P (2011) Physics of Life: The Dawn of Quantum Biology. Nature 474: 272-274.[Crossref].
- Zhang WR (2011) YinYang Bipolar Relativity: A Unifying Theory of Nature, Agents and Causality with Applications in Quantum Computing, Cognitive Informatics and Life Sciences. IGI Global, Hershey and New York, 2011.
- Zhang WR, Peace KE (2014) Causality Is Logically Definable — Toward an Equilibrium-Based Computing Paradigm of Quantum Agent and Quantum Intelligence (QAQI) (Survey and Research). Journal of Quantum Information Science 4: 227- 268. DOI: 10.4236/jqis.2014.44021
- Rosenfeld S (2013) Group consensus theorem and self-organized criticality: unifying principles for understanding self-organization, swarm intelligence and mechanisms of carcinogenesis. Gene Regul Syst Biol 7, 23–39. [Crossref]
- Rosenfeld S (2015) Critical junction: Nonlinear dynamics, swarm intelligence and cancer research. Fractal Geometry and Nonlinear Anal in Med and Biol 1: 7-10.
- Mandelbrot B (1982) The Fractal Geometry of Nature, W H Freeman & Co, 1982.
- Dirac P (1930) The principle of Quantum Mechanics. Oxford University Press Inc., (4th Edn), New York, Reprinted 2004.
- Einstein A (1954) Sonja Bargmann, translator. Ideas and Opinions, pp. 266-270. Wings Books, New York NY, 1954.
- Bohr N (1948) On The Notions of Causality and Complementarity. Dialectica 2: 312-319.
- Smolin L (2005) The case for background independence. Jul 2005. arXiv:hep-th/0507235v1.
- Zhang WR (2012a) YinYang Bipolar Atom – An Eastern Road toward Quantum Gravity. J of Modern Physics 3: 1261-1271. DOI: 10.4236/jmp.2012.329163
- Zhang WR (2012b) Beyond Spacetime Geometry – The Death of Philosophy and Its Reincarnation. J of Modern Physics 3: 1272-1284. DOI: 10.4236/jmp.2012.329164
- Zhang WR (2013) Bipolar Quantum Logic Gates and Quantum Cellular Combinatorics – A Logical Extension to Quantum Entanglement. J of Quantum Information Science 3: 93-105. DOI: 10.4236/jqis.2013.32014
- Zhang WR, Peace KE (2013) Revealing the Ubiquitous Effects of Quantum Entanglement – Toward a Notion of God Logic. J of Quantum Information Science 3: 143-153. DOI: 10.4236/jqis.2013.34019
- Zhang WR (2003a) Equilibrium Relations and Bipolar Cognitive Mapping for Online Analytical Processing with Applications in International Relations and Strategic Decision Support. IEEE Trans on SMC Part B33: 295-307. [Crossref]
- Zhang WR (2003b) Equilibrium Energy and Stability Measures for Bipolar Decision and Global Regulation. Int’l J of Fuzzy Sys 5: 114-122.
- Zhang WR, Zhang L (2004) YinYang Bipolar Logic and Bipolar Fuzzy Logic. Information Sciences 165: 265-287.
- Zhang WR, Zhang HJ, Shi Y, Chen SS (2009) Bipolar Linear Algebra and YinYang-N-Element Cellular Networks for Equilibrium-Based Biosystem Simulation and Regulation. J of Biological Systems 17: 547-576.
- Boole G (1854) An Investigation of the Laws of Thoughts. MacMillan, London, 1854. Reprinted by Dover Books, New York, 1854.
- Zadeh LA (1965) Fuzzy sets. Information and Control 8: 338–353.
- Girard JY (1987) Linear logic. Theoretical Computer Science 50: 1–102.
- Einstein A, Podolsky B, Rosen N (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 47: 777-780.
- Zhang WR, Marchetti F (2015a) YinYang bipolar quantum geometry and bipolar quantum superposition Part II – Toward an equilibrium-based analytical paradigm of quantum mechanics and quantum biology. Fractal Geometry and Nonlinear Anal in Med and Biol 1. 69-77. DOI: 10.15761/FGNAMB.1000113
- Zhang WR, Marchetti F (2015b) A Logical Exposition of Dirac 3-Polarizer Experiment and Its Potential Impact on Computational Biology. Proceedings of ACM Conference on Bioinformatics, Computational Biology, and Health Informatics (ACM BCB) – 2015, 517-518. DOI: 10.1145/2808719.2811438