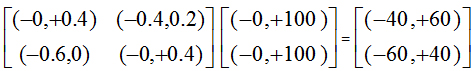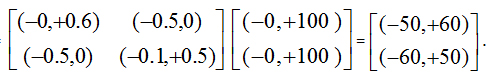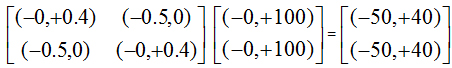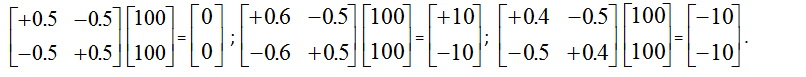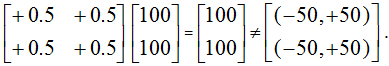Abstract
In Part I of this paper, YinYang bipolar quantum agent (BQA), bipolar quantum geometry (BQG) and 2-dimensional generic bipolar quantum superposition are introduced with a geometrical and logical exposition of Dirac 3-polarizer experiment. While the exposition qualifies BQG as a geometry of light, it is shown in this paper that the logical exposition can be extended to an analytical paradigm of quantum mechanics and quantum biology. It is shown that BQG as the geometry of light is also the geometry of Nature with a logical unification of matter and antimatter atoms into a bipolar quantum cellular automaton (BQCA) through multidimensional YinYang bipolar quantum superposition using bipolar quantum linear algebra (BQLA). With the BQCA interpretation of quantum mechanics, it is shown matter and antimatter self-organization and spacetime emergence is logically possible within BQG. A scalable BQCA model for biological repression-activation and/or degeneration-regeneration is introduced. Bipolar cellular division and bipolar fractality are proposed. Background independent normal and abnormal bipolar fractal branching is proposed. A discussion on quantum gravity and mathematical abstraction is presented. A few challenges and predictions are posted. It is contended that BQA, BQG, BDL, BQLA, and BQCA constitute an analytical paradigm of quantum mechanics and quantum biology that may contribute to equilibrium-based analysis of quantum decoherence and collapse as associated with quantum measurement.
Key words
bipolar quantum linear algebra, multidimensional bipolar quantum superposition, bipolar quantum cellular automaton, background independence, equilibrium-based bipolar fractality, analytical quantum biology, quantum gravity, five challenges for a theory of everything, falsifiability
Introduction
In Part I [1] bipolar quantum agent (BQA), bipolar quantum geometry (BQG) and bipolar quantum superposition (BQS) are introduced based on bipolar dynamic logic (BDL) and bipolar quantum linear algebra (BQLA) [2-5]. BQG, BDL and BQS have led to a logical exposition of Dirac 3-polarizer experiment [6]. The logical exposition suggests that BQG can serve as a geometry of light. The exposition, however, could be deemed isolated and accidental unless the result can be mathematically and physically generalized. This paper presents such a generalization. We show that BQG can be further extended to an analytical paradigm of quantum mechanics and quantum biology.
While research in fractal geometry [7] has been focused on nonlinear analysis of geometric patterns with self-similarity/self-affinity, background independent geometry [8] is advocated in quantum gravity research for spacetime emergence. Both approaches have so far stopped short of providing a formal logical foundation for physics [9]. Thus, the following questions can be raised:
- What is the quantum nature of biological regeneration and degeneration?
- Can quantum mechanics be logically unified with quantum biology?
- What is the quantum nature of agents and fractals?
- Is the geometry of Nature really fractal? [10]
This paper attempts to provide answers to the above fundamental questions. It is shown in Section 2 that BQG as a geometry of light is also the geometry of Nature. Section 3 presents a bipolar quantum cellular automaton (BQCA) interpretation of quantum mechanics. Equilibrium-based fractality is conceptualized. Section 4 presents a discussion on quantum gravity and mathematical abstraction with a few challenges and predictions. Section 5 includes a few conclusion remarks.
From a geometry of light to the geometry of Nature
Since all previous logical systems before BQG and BDL failed to provide a systematic logical exposition of Dirac 3-polarizer experiment, BQG is qualified to be a geometry of light. If it is also proven a geometry of matter and antimatter atoms, BQG can be regarded as the geometry of Nature. Before then, in this section we show the following:
(1) Bipolar quantum entanglement can be logically defined with BDL in BQG for spacetime emergence;
(2) Energy and information can be unified with bipolar representation;
(3) Matter-antimatter atoms can be unified with a cellular automaton interpretation of quantum mechanics.
Bipolar quantum entanglement and spacetime emergence
Quantum entanglement is another key concept in quantum mechanics closely related to quantum superposition. Due to its lack of locality and causality, Einstein once called it “spooky action in a distance” and questioned the completeness of quantum mechanics [11].
While all previous logical systems so far failed to provide a logical definition for quantum entanglement. The complete background independent property of BQG makes such a logical definition possible with BDL. A key element of BDL is bipolar universal modus ponens (BUMP) – a bipolar dynamic generalization of modus ponens (MP) [2,12] which states that, 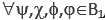
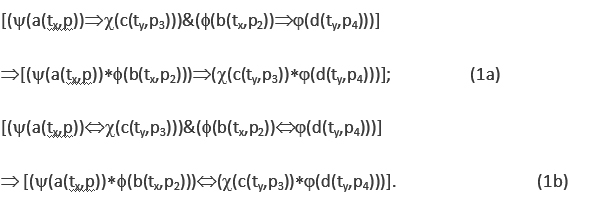
In Eq. ( are bipolar predicates; * is a bipolar universal operator that can be bound to any binary operator in BDL; Þ is bipolar implication; a(tx,p), b(ty,p2), c(tx,p3), d(ty,p4) are bipolar quantum agents where a(t,p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in spacetime). An agent p without time and space is assumed at any time t and space p. An agent at time t and space p is therefore more specific.
are bipolar predicates; * is a bipolar universal operator that can be bound to any binary operator in BDL; Þ is bipolar implication; a(tx,p), b(ty,p2), c(tx,p3), d(ty,p4) are bipolar quantum agents where a(t,p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in spacetime). An agent p without time and space is assumed at any time t and space p. An agent at time t and space p is therefore more specific.
BUMP reads: 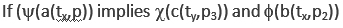 implies
implies 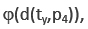 then the bipolar interaction
then the bipolar interaction 
If the bipolar implication operator Þis replaced with the bipolar equivalence operator Û, BUMP becomes a logical form of quantum entanglement as shown in Eq. 1(b). The logical form of bipolar quantum entanglement qualifies BDL as a causal logic for equilibrium-based bipolar deduction. On the other hand, BQG and BDL supports the fundamental concept of quantum superposition and entanglement for spacetime emergence as a dynamic equilibrium of Nature’s Yin and Yang.
Bipolar energy/information and bipolar quantum linear algebra (BQLA)
While BDL is logical but not fully mathematical, BQLA leads to an algebraic unification of bipolar energy/information [13-15] that in turn leads to formal algebraic definitions of equilibrium and harmony for revealing the ubiquitous effects of quantum superposition and entanglement [2,15-19].
Given bipolar quantum agent e=(e-, e+)Î [-∞, 0] × [0, +∞],
- The Yin or negative energy/information: ε−(e) = e-;
- The Yang or positive energy/information: ε+(e) = e+;
- Equilibrium: (e-, e+) when e- = - e+;
- Eternal Equilibrium: (0,0);
- Bipolar Energy/information: ε(e) = (ε−(e),ε+(e)) = (e-, e+);
- Total Energy/information: |ε|(e) = |ε−|(e) + |ε+|(e) = |e-| + |e+|;
- Imbalance: εimb(e)=|ε+|(e) -|ε-|(e);
- Balance: (|ε|(e)−|εimb(e)|)/2.0 = min(|e-|, |e+|);
- Harmony: (|ε|(e) − |εimb(e)|)/|ε|(e).
Elementary energy/information measures can be extended to system energy/information measures with BQLA[2]. Each row, column, or a whole matrix in BQLA can have negative, positive and bipolar energy/information with absolute total and balance [16]. These measures lead to the unification of energy and information as well as system level equilibrium and harmony. This is discussed in the next section.
Bipolar quantum cellular automaton unification of matter-antimatter
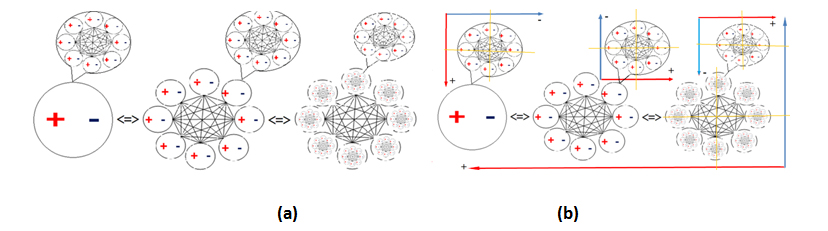
The concepts of bipolar elementary energy and information laid a basis for modeling bipolar quantum superposition of multiple bipolar quantum agents (BQAs) (cf. Part I) as a multidimensional dynamic equilibrium with bipolar quantum linear algebra (BQLA). Figure 1 shows that two or more bipolar variables can be integrated into a multidimensional bipolar quantum superposition. Eq. 2(a-b) provide some basic algebraic equations for the bipolar quantum superposition of multiple BQAs; Eq. 2(c) defines system level quantum superposition with BQLA matrix multiplication; Eq. 2(d) defines a bipolar quantum power law.
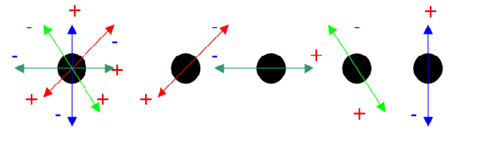
Figure 1. Multidimensional equilibrium of bipolar quantum agents
∀(x, y), (u, v) ∈ B∞ = [−∞, 0] × [0, +∞], we have
Bipolar Addition: (x, y) + (u, v) ≡ (x + u, y + v). (2a)
Bipolar Multiplication: (x, y) × (u, v) ≡ (xv + yu, xu + yv); (2b)
Bipolar Linear Algebra: E(t+1) = M(t)´ E(t). (2c)
Bipolar Dynamic Power Law: E(t+n) = Mn(t) ´ E(t). (2d)
In Eq. (2c) M(t) is a bipolar quantum logic gate matrix [18] that characterizes the nucleus bipolar regulation center of the electron-positron pairs of a matter or antimatter atom; E(t) is the bipolar energy vector of the pairs of an atom. The unification is realized in the background independent BQG (cf. Part I). Figure 2 shows an equilibrium-based unification of matter and antimatter atoms as a bipolar quantum cellular automaton (BQCA) – a multidimensional bipolar dynamic equilibrium emerged from bipolar interaction and bipolar quantum superposition.
The matter-antimatter BQCA unification can be deemed a result of self-organization of multiple BQAs through bipolar quantum superposition in BQG. It is shown that the BQCA also leads to the unification of wave-particle duality [15,16]. Thus, not only can BQG serve as a geometry of light, it can also serve as the geometry of Nature.
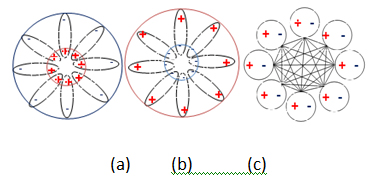
(a) (b) (c)
Figure 2. (a) Matter atom as bipolar quantum agent; (b) Antimatter atom as bipolar quantum agent; (c) Bipolar equilibrium-based unification of matter and antimatter into a bipolar cellular automaton (adapted from [2,16])
Toward an analytical paradigm of quantum mechanics and quantum biology
In this section we show that the BQCA model for matter-antimatter unification presented in last section can be scaled to physical and biological system models with conservational, regenerating, degenerating or repression and activation properties. These properties make it possible to describe different biological systems as BQAs at the molecular, cell and organism levels.
Scalable fractality of BQCA
Without a formal geometrical and logical basis for quantum mechanics, after seven decades since its inception, quantum biology [20] is still a research area in its infancy. Although the Yin and Yang of Nature have been recognized as fundamental and ubiquitous bipolar coexistence in biology [21] and genomics [22], no formal geometrical and logical model had been available for reasoning on the Yin and Yang for thousands of years until recently. It is a living proof to Einstein’s assertion [23] that “the axiomatic basis of theoretical physics cannot be extracted from experience but must be freely invented.”
The above dilemma can be best illustrated with two mysteries. One is in the process of photosynthesis where “Particles of light called photons, streaming down from the Sun, arrive randomly at the chlorophyll molecules and other light-absorbing ‘antenna’ pigments that cluster inside the cells of every leaf, and within every photosynthetic bacterium. But once the photons’ energy is deposited, it doesn’t stay random. Somehow, it gets channeled into a steady flow towards the cell’s photosynthetic reaction centre, which can then use it at maximum efficiency to convert carbon dioxide into sugars.”[cf. 24] In such a way, tree leaves as biological fractals can grow and become greener in spring and summer. The maximum efficiency eventually fades away and they may have to change color from green to yellow in the fall. In quantum biology research, however, we still do not have a quantum mechanical model for biological growth and aging. It is still a mystery how exactly the incoming photons can contribute to the inner working of photosynthesis. Another mystery is in birds’ ability in navigating between the far north and the far south. Scientists have found that such navigation ability is based on the magnetic field of the Earth [cf. 24], but how such biological intelligence is related to the quantum world remains an unsolved mystery.
Mathematically, "(x,y),(u,v)ÎB1,BF,B∞, (x,y) as a logical or mathematical characterization of bipolar quantum superposition presents an equilibrium-based quantum unification of biological agents and their environments at different levels of granularity. Therefore, the BQCA in Figure 2(c) can be scaled to molecule, cell and system levels through further superposition and entanglement (Figure 3). At the quantum level, (x,y) can be the elementary bipolar energy of an electron-positron pair within an atom. At the atomic level, (x,y) can be the total bipolar energy of all the bipolar pairs within an atom. At the molecule, cell or organism levels, (x,y) can be the total bipolar energy of all the bipolar pairs of a lower level. With this unification, two bipolar variables (x,y) and (u,v) can be interactive through bipolar quantum superposition or entanglement. Thus, internal and external bipolar interaction can be posited as the source of causality for biological and mental functionalities with formal bipolar equilibrium-based definability.
Theorem 1: A bipolar equilibrium-based BQCA with bipolar fractality is scalable.
Proof: Since a BQCA as an BQA can emerge as a bipolar dynamic equilibrium per Axiom 3(cf. Part I) that may consist of subsystems in bipolar equilibrium or non-equilibrium states, the theorem follows from that (1) for a normal globally regulated biological system, the global bipolar equilibrium or non-equilibrium of energy/information is mathematically the total of the local ones of the subsystems that may show properties of self-organization, regeneration, and degeneration; (2) for an abnormal biological system or fractal, the local equilibrium or non-equilibrium of the subsystems may be out of global regulation but can still exhibit local scalability and bipolar fractality.
Theorem 1 shows that BQG presents a unified geometrical and analytical basis for quantum mechanics, quantum biology, and quantum fractality with nonlinear dynamic normal or abnormal bipolar fractality. Figure 3 shows that the background independent nature of BQG makes it possible to host bipolar fractals for qualitative and quantitative analysis anywhere and anytime. While geometric shapes or patterns have been a focus in the fractal geometry of Nature [7], the background independent nature of BQG bridges a gap from the fractals of Nature to the quantum nature of fractals and vice versa. With bipolar quantum geometry, biological conservation, growing or aging processes can be modeled with nonlinear bipolar dynamic input/output processes such as the inner workings of photosynthesis. It has the potential for bipolar quantum swarm intelligence at the system, cell, molecular, atom, and quantum levels as well, which may find applications in life sciences such as cancer research [25,26].
- (b)
Figure 3. Equilibrium-based bipolar scalability and fractality of BQCA: (a) Bipolar scalability and fractality; (b) BQG as a background independent bipolar fractal geometry
With complete background independence, BQG makes bipolar quantum cellular automaton-based fractal emergence, branching, regulation, and communication possible through bipolar quantum superposition and entanglement. In BQG, spacetime can emerge and disappear following the arrivals and departures of BQAs or fractals. A BQA as a dynamic equilibrium is to the Yin and the Yang of bipolar relativity as gravity is to space and time of general relativity but with fundamentally different syntax, semantics, and basic postulates. While space and time are not direct opposites and cannot form a bipolar dynamic equilibrium, bipolar interaction and complementarity is posited to cause the emergence of BQAs as well as spacetime through bipolar quantum superposition and entanglement in a bipolar dynamic equilibrium process [1,2].
Since the Yin and the Yang are two reciprocal and interdependent opposites of a dynamic equilibrium that are completely background independent and ubiquitous, BQG is fundamentally different from Euclidian, Hilbert, and spacetime geometries. The new geometry is quadrant-irrelevant and shape-free because bipolar identity, interaction, superposition, separation, and entanglement can be accounted for in the geometry without quadrants. With the shape-free and quadrant-irrelevant properties, BQG can support bipolar fractality anywhere in any amount of bipolar energy or information for investigating into the quantum nature of shaped fractals in micro and meso scales. Shapes and quadrants can, however, be added where observer is involved and background dependent information is needed. Thus, BQG can subsume other geometries and can be used to reason on space and time as well.
BQCA regulation for energy/information conservation
A physical or biological system can be regulated to maintain energy/information conservation. When the absolute total energy of each row (|ε|Mi,*(t)) and each column (|ε|M*,j(t)) of the regulatory matrix M(t) equals 1.0, M(t) is defined as a generalized unitary bipolar quantum logic gate matrix extended from integer domain to decimal domain [18]. Such a quantum logic gate exhibits energy/information conservation regulatory functionality. That is, if "i,j, |ε|Mi,*(t) = |ε|M*,j(t) = 1.0, we have
|ε|E(t+n) = |ε|(Mn(t) ´ E(t)) º|ε|E(t). (3)
Eq. 3 can be deemed a dynamic equilibrium process with bipolar energy/information conservation in absolute values but does not have to maintain bipolar balance (or generalized CP symmetry). This is illustrated as follows:
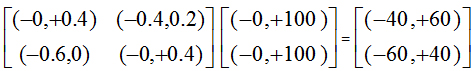
Row energies of M(t):
|ε|((-0, +0.4)(-0.4, +0.2)) = 0.4 + |-0.4| + 0.2 = 1.0;
|ε|((-0.6, +0)(-0, +0.4,)) = |-0.6| + 0.4 = 1.0;
Column energies of M(t):
|ε|((-0, +0.4)(-0.6, 0)) = 0.4 + |-0.6| = 1.0;
|ε|((-0.4, +0.2)(-0, +0.4)) = |-0.4| + 0.2 + 0.4 = 1.0;
Energies of E(t) and E(t+1):
|ε|E(t) = 100 + 100 = 200;
|ε|E(t+1) =|-40|+60+|-60|+40 =200 = |ε|E(t).
BQCA regulation for biological activation and regeneration.
The ubiquitous Yin Yang 1 regulator protein acts as both a repressor and an activator in gene expression regulation [22]. Thus, the functionality of the regulator can be characterized as a bipolar variable (yin, yang).Activation regulation may lead to biological growth. When the absolute total energy of each row and each column of the organizational matrix M(t) is greater than 1.0, it exhibits such regeneration regulatory functionality. If "i,j, |ε|Mi,*(t) >1.0 and |ε|M*,j(t) > 1.0, we have
|ε|E(t+n) = |ε|(Mn(t) ´ E(t)) >|ε|E(t+n-1). (4)
Eq. 4 can be deemed a biological growing or nuclear fission process. This is illustrated as follows:
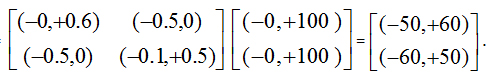
Row energies of M(t):
|ε|((-0, +0.6)(-0.5, 0)) = 0.6 + |-0.5| = 1.1;
|ε|((-0.6, +0)(-0, +0.5,)) = |-0.6| + 0.5 = 1.1;
Column energies of M(t):
|ε|((-0, +0.6)(-0.5, 0)) = 0.6 + |-0.5| = 1.1;
|ε|((-0.5, +0)(-0.1, +0.5,)) = |-0.5| + |-0.1| + 0.5 = 1.1;
Energies of E(t) and E(t+1):
|ε|E(t) = 100 + 100 = 200;
|ε|E(t+1) =|-50|+60+|-60|+50 =220 >|ε|E(t) .
BQCA regulation for biological repression/degeneration
Repression (Yin) is the opposite of activation (Yang) of the ubiquitous Yin Yang 1 regulator protein [22]. Such regulation may lead to biological degeneration or aging. When the absolute total energy of each row and column of the organizational matrix M(t) is less than 1.0, it exhibits such degeneration regulatory functionality. That is, If "i,j, |ε|Mi,*(t) < 1.0 and |ε|M*,j(t) <1.0, we have
|ε|E(t+n) = |ε|(Mn(t) ´ E(t)) <|ε|E(t+n-1). (5)
Eq. 5 can be deemed a biological degeneration or nuclear decay process. This is illustrated as follows:
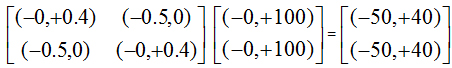
Row energies of M(t):
|ε|((-0, +0.4)(-0.5, 0)) = 0.4 + |-0.5| = 0.9;
|ε|((-0.5, +0)(-0, +0.4,)) = |-0.5| + 0.4 = 0.9;
Column energies of M(t):
|ε|((-0, +0.4)(-0.5, 0)) = 0.4 + |-0.5| = 0.9;
|ε|((-0.5, +0)(-0, +0.4,)) = |-0.5| + 0.4 = 0.9;
Energies of E(t+1) and E(t):
|ε|E(t) = 100 + 100 = 200;
|ε|E(t+1) =|-50|+40+|-40|+50 =180 >|ε|E(t).
Bipolar cell division and equilibrium-based bipolar fractal branching
In a growing process, after n growing cycles, the energy |ε|E(t+n) = |ε|(Mn(t) ´ E(t)) might be high enough for a biological agent to divide into two or more agents. For instance, a cell may grow and divide into two cells. This can be mathematically characterized with Eq. 6 and depicted in Figure 4.
Bipolar cellular linear division: E Þ ½(E) + ½(E) (6)
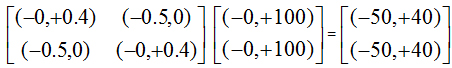
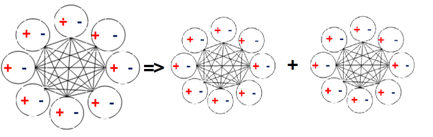
Figure 4. Bipolar cellular division in a growing process
After a cellular division, each bipolar vector can be regulated by its own bipolar regulatory matrix Mi as a local regulation center for further energy conservation, growth, cell division or degeneration. All the local regulation centers can be regulated by a global regulation center MG. Eq. 7(a) shows an example power law in this case. Assuming there are k elements for each BQCA,Eq. 7(b) shows the total energy of a BQCA after division.

|ε|E(t) = |ε|Ei(t)). (7b)
In normal growth, all Ei are regulated by the global regulation center MG. Otherwise, some Ei could be out of control with abnormal growth. With energy conservational, regenerating and degenerating quantum logic gates, global activation/repression is logically achievable with a quantum logic network of bipolar quantum cellular automatons.
Bipolar cell division 2021 Copyright OAT. All rights reservractal branching. An equilibrium-based principle of normal and abnormal bipolar fractal branching is derived as follows.
Bipolar fractal branching principle: In a normal bipolar fractal branching, a BQCA observes the bipolar dynamic equilibrium condition, where the absolute energy of the BQCA equals to the total of all its branches or elements at any time t regardless of local bipolar balance or imbalance. Otherwise, there must be abnormal bipolar fractal branching with unregulated growth in a non-equilibrium state.
Theorem 2: A necessary but insufficient condition of normal bipolar fractal branching is branching toward the eternal equilibrium state (0,0) of BQG.
Proof: If the condition is violated, the energy of a branch would be greater than that of the BQCA itself and the branching would be abnormal. Therefore, the condition is necessary. The condition is insufficient because it does not guarantee the total energy of all branches and elements to be equal to that of the BQCA itself at any time.
Figure 5(a) shows a sketch of normal bipolar fractal branching of a single branch where bole is greater than branch; Figure 5(b) shows a sketch of abnormal case where branch is greater than bole. Evidently, normal or abnormal bipolar fractal branching can be quantized, plotted, and analyzed within the equilibrium-based and background independent BQG but that is impossible without bipolarity in other geometries.

Figure 5. Single normal and abnormal bipolar fractal branching in BQG
3.5 Bipolar dynamic equilibrium – the essence of being and causality
While truth has been deemed the essence of being since Aristotle, without bipolarity truth-based logic and linear algebra are incapable of bipolar causal interaction, self-organization, and dynamic regulation for energy-information conservation, degeneration, regeneration and oscillation due to bipolar cancelation. For instance,
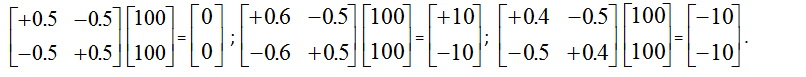
The above examples clearly show that, without bipolar regulation, bipolar equilibrium-based information and/or energy conservation, regeneration, linear division, and degeneration are impossible using classical linear algebra.
Of course, we can attempt to use a positive regulation matrix. But a positive matrix does not show bipolar interaction and balancing cause-effect relation toward a bipolar dynamic equilibrium, non-equilibrium or oscillating state [2,16]. For instance,
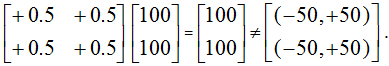
From the above, it is clear that (-,+) bipolarity is a key for bipolar causality, bipolar quantum superposition and bipolar quantum entanglement. It provides a holistic, unitary, and analytical framework of quantum mechanics and quantum biology for the complex interaction and regulation of quantum agents with an equilibrium-based scalable quantum automata theory [2,15,16,18]. While quantum mechanics heavily relies on probability and do not lend itself as an analytical system, the analytical nature of the bipolar equilibrium-based approach provides a geometrical and logical basis toward a computational paradigm of quantum agents, quantum biology and quantum intelligence [15].
Discussion
On quantum foundation
Einstein asserted [27]: “Physics constitutes a logical system of thought which is in a state of evolution, whose basis (principles) cannot be distilled, as it were, from experience by an inductive method, but can only be arrived at by free invention.” He affirmed [23]: “Pure thought can grasp reality” and “Nature is the realization of the simplest conceivable mathematical ideas.” He reasserted [9]: “For the time being we have to admit that we do not possess any general theoretical basis for physics which can be regarded as its logical foundation.”
In light of the above, BQG and BDL has been proposed as an equilibrium-based geometrical and logical foundation for quantum physics and biophysics with an equilibrium-based interpretation of quantum superposition. Although it is questionable whether the equilibrium-based geometrical and logical system is what Einstein sought for physics in the last century, BQG has been proven completely background independent (cf. Part I) and BDL has been proven a bipolar dynamic generalization of Boolean logic (BL). It has been show that the two together leads to an analytical paradigm of quantum mechanics and quantum biology. Furthermore, BDL does satisfy the simplicity criterion set forth by Einstein and has passed a major falsifiability test with a logical exposition ofthe longstanding puzzle of Dirac 3-polarizer experiment.
While background independent geometry has been advocated by Lee Smolinin the quest for quantum gravity [8], no formal logical system has been reported for completely background independent geometrical reasoning with logically definable causality besides BDL [2]. A distinguishing factor lies in YinYang bipolar complementarity. No matter time is real or unreal, fundamentally different from the Yin and the Yang of Nature, space and time are not bipolar interactive and cannot form bipolar dynamic equilibrium, symmetry or quantum superposition for quantum gravity. This could be the reason why other approaches to quantum gravity so far stopped short in finding a unique logical foundation as a general theoretical basis for physics. It is contended that the equilibrium-based approach has opened an Eastern road toward quantum gravity [2,16] and will lead to a quantum reincarnation of philosophy [17].
Remarkably, a cellular automaton interpretation of quantum mechanics is proposed and strongly advocated by Gerardus ‘t Hooft [28]. ‘t Hooft points out that “Einstein may still have been right, when he objected against the conclusions drawn by Bohr and Heisenberg. It may well be that, at its most basic level, there is no randomness in nature, no fundamentally statistical aspect to the laws of evolution. Everything, up to the most minute detail, is controlled by invariable laws. Every significant event in our universe takes place for a reason, it was caused by the action of physical law, not just by chance.” ‘t Hooft stated: “We set up a systematic study of the Cellular Automaton Interpretation of quantum mechanics. We hope to inspire more physicists to do so, to consider seriously the possibility that quantum mechanics as we know it is not a fundamental, mysterious, impenetrable feature of our physical world, but rather an instrument to statistically describe a world where the physical laws, at their most basic roots, are not quantum mechanical at all.” However, ‘t Hooft conceded: “Sure, we do not know how to formulate the most basic laws at present, but we are collecting indications that a classical world underlying quantum mechanics does exist.”
Now, BDL and BQLA have led to a bipolar quantum cellular automaton (BQCA) interpretation of quantum mechanics. Not only has BQCA logically unified matter and antimatter atoms [16], it also has led to a cellular model for quantum biology with scalable bipolar quantum fractality. BQCA is expected to serve as a mathematical basis for swarm quantum intelligence as well. Some questions remain, however, including:
- whether the world modeled with BQCA can be regarded as a classical world underlying quantum mechanics sought by ‘t Hooft [28];
- whether BQCA will lead to swarm quantum intelligence for solving some mysteries in quantum biology such as the ability of birds to navigate using Earth’s magnetic field or the puzzle of the inner workings in photosynthesis [24];
- whether the BQCA model constitutes a fundamental departure from quantum decoherence and collapse theories associated with quantum measurement.
While all three questions are gigantic research topics. The third one is a most critical one for quantum computing. The BQCA interpretation of quantum mechanics provides an equilibrium-based analytical basis for quantum measurement, decoherence and collapse. Without bipolarity, there seems to be no way to call upon anything external factor to disrupt the autonomous evolution of a quantum entanglement in the existing decoherence and collapse theories in quantum mechanics [cf. 29]. With bipolarity, however, all quantum and gravitational action-reaction or negative-positive energies can be blended together into an energy/information conservational or non-conservational bipolar quantum gate matrix for generalized-CPT (G-CPT) [15] symmetry analysis which may leads to a solution to the collapse problem.
Notably, limitations of fractal geometry have been identified. In particular, experimental result shows that the many orders of magnitude of the fractal power law described in the seminal book by Mandelbrot [7] are not supported in an unequivocal way by data collected [10]. While this limitation is observed in macro scales, bipolar quantum geometry provides a platform for investigating into the quantum nature of fractals. It is interesting to ask: If the universe is a bipolar quantum fractal in a dynamic equilibrium, does the order of magnitude of a quantum fractal power law have to have an upper limit?
Since fractals in Nature exhibit statistical similarity with a heavy role of chance, how fractals can have deterministic property is another question. A possible answer is that certain statistical similarity at macro scales of Nature can be caused by bipolar quantum superposition of the different types of particles in different combinations at the meso scales. The unlimited number of combinations may lead to the nondeterministic property at a higher level. But at the quantum level, some (not all) fundamental properties might be deterministic such as bipolar equilibrium and non-equilibrium conditions.
On mathematical abstraction
Philosophically, truth has been asserted as the essence of being since Aristotle. Following this assertion, the negative sign used to be forbidden in mathematics and is still largely forbidden in truth-based logical reasoning because – 1 is widely deemed isomorphic to +1.
Is -1 isomorphic to +1? Is truth the essence of being and Nature? Could BDL be the logic of physics? Could the essence of being be bipolar dynamic equilibrium (a bipolar quantum superposition or entanglement)? To answer these questions, we need to recall some historical event. According to the BBC, we have the following “mystery and suspicion” [31]:
“In 1759 the British mathematician Francis Maseres wrote that negative numbers ‘darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple.’ Because of their dark and mysterious nature, Maseres concluded that negative numbers did not exist, as did his contemporary, William Friend. However, other mathematicians were braver. They took a leap into the unknown and decided that negative numbers could be used during calculations, as long as they had disappeared upon reaching the solution.
“The history of negative numbers is one of stops and starts. The trailblazers were the Chinese who by 100 BC were able to solve simultaneous equations involving negative numbers. The Ancient Greeks rejected negative numbers as absurd, by 600 AD, the Indians had written the rules for the multiplication of negative numbers and 400 years later, Arabic mathematicians realized the importance of negative debt.
“But it wasn't until the Renaissance that European mathematicians finally began to accept and use these perplexing numbers.
“Why were negative numbers considered with such suspicion? Why were they such an abstract concept? And how did they finally get accepted?”
It is pointed out [2] that the debate on truth, bipolarity and isomorphism can be deemed a continuation of the debate on negative numbers extended to the logical arena. The negative sign “-” should not be forbidden as part of a bipolar equilibrium-based dynamic logic unless (1) mathematicians and logicians would be willing to ask their children to learn math without it; (2) scientists would say particle and antiparticle are isomorphic; (3) car owners would like the two poles of their car batteries being labeled with +,+; ( 4) philosophers would say Yin is isomorphic to Yang; (5) psychiatrist would say depression is isomorphic to mania. Otherwise, the so-called -+ isomorphism is not a scientific principle that enhances the strictness of science but a kind of socially constructed entrenched noble hypocrisy that hinders a new mathematical abstract ion for scientific unification.
Challenges and predictions
Theoretical physics is at a crossroad. While string theory, M-theory and loop theory have been advocated in modern physics as three candidates for the theory of everything, the three candidates have so far failed the falsifiability test. YinYang bipolar relativity [2] is proposed as a quantum gravity theory but not a theory of everything because it does not posit any smallest elementary particle like strings or loops. What it posits is Nature’s bipolarity as the most fundamental property of everything and bipolar dynamic equilibrium as the essence of being. Thus, YinYang bipolar relativity provides an open-world and open-ended approach to quantum gravity for knowledge discovery.
YinYang bipolar relativity has led to a number of specific hallenges to the candidate theories of everything. Since acceleration is equivalent to gravitation under general relativity, any physical, social, mental, and biological acceleration such as growth and aging are qualified to be a kind of quantum gravity. It is further argued that as a most fundamental scientific unification not only can quantum gravity be applied in physical science, but also in computing science, social science, brain science, and life sciences as well [2, p224]. Thus, we post five challenges to the candidate theories of everything to enhance their falsifiability.
Challenge 1: A valid theory of everything should subsume a logical quantum gravity sub-theory that can provide a fundamental quantum geometry and a logical exposition of Dirac 3-polarizer experiment with simple logical interpretations and definitions for quantum superposition, quantum entanglement, and quantum causality.
Challenge 2: A valid theory of everything should subsume a physical quantum gravity sub-theory that provides a scalable quantum cellular automaton interpretation of quantum mechanics that leads to the unification of matter and antimatter as well as wave and particle.
Challenge 3: A valid theory of everything should subsume a mental quantum gravity sub-theory that provides a logical interpretation for psychiatric disorders such as bipolar disorders.
Challenge 4: A valid theory of everything should subsume a biological quantum gravity sub-theory that provides a unification for quantum biology, quantum computing and quantum intelligence.
Challenge 5: A valid theory of everything should subsume a social quantum gravity sub-theory that provides a unified mathematical model for socio-economics, bio-economics and bio-quantum computing.
It is our view that the so-called “theory of everything candidates” have so far stopped short of passing the above falsifiability tests. We post the following predictions for falsification:
Prediction 1: BDL is the minimal but most general logical foundation for physics.
Prediction 2: The nature of quantum superposition and entanglement is bipolar complementarity; the essence of being is bipolar dynamic equilibrium.
Prediction 3: YinYang bipolar quantum geometry is the geometry of light and Nature. Any other geometry is likely to be phenomenal and less fundamental albeit very useful and influential.
Prediction 4: The universe is a bipolar quantum cellular automaton of negative-positive energies in bipolar dynamic equilibrium.
Prediction 5: The wave-function collapse problem associated with quantum measurement is fundamentally the loss of bipolar dynamic equilibrium in a quantum entanglement.
Conclusions
Based on Part I of this paper, it has been shown that BQG, BDL and BQLA lead to a bipolar quantum cellular automaton (BQCA) interpretation of quantum mechanics and quantum biology. Bipolar quantum entanglement has been logically defined; dynamic self-organization of matter and antimatter into a BQCA has been illustrated with multidimensional bipolar quantum superposition; scalability and fractality of BQCA has been conceptualized. An equilibrium-based analysis of quantum decoherence has been presented. It is contended that BQA, BQG, BDL, BQLA, and BQCA constitute an analytical paradigm of quantum mechanics and quantum biology.
It has been shown that biological cellular division, energy growth and degeneration can be regulated with bipolar repression and activation, respectively. Background independent normal and abnormal bipolar fractal branching have been proposed. Repression-activation regulation of BQCA for regeneration and degeneration exhibits potential for swarm quantum intelligence [cf. 15,25,26].
A discussion on scientific unification has been presented. Lee Smolin’s background independence, Gerardus ‘t Hooft’s cellular automaton interpretation of quantum mechanics, and the order of magnitude of fractal power laws have been briefly discussed. BBC’s “mystery and suspicion” on negative numbers has been reviewed for pondering some issues about truth, polarity, and isomorphism. A few challenges and predictions have been posted.
Without a formal geometrical and logical basis for quantum superposition and quantum entanglement, quantum mechanics has been paradox-prone and quantum biology has remained a research area in its infancy for decades. YinYang bipolar quantum geometry and bipolar dynamic logic has provided an equilibrium-based geometrical and logical basis toward a unifying analytical paradigm of quantum mechanics and quantum biology as well as quantum computing and quantum communication with multidimensional bipolar quantum superposition. Among many of the open research topics, swarm quantum intelligence is expected to hold the potential for significant advancement of science and technology especially quantum biology and medicine and thus deserves further investigation.
Acknowledgement
The authors acknowledge the Editor-in-Chief and the anonymous reviewers of this journal for their critical and constructive comments on earlier versions of this paper.
References
- Zhang WR, Marchetti F (2015) YinYang bipolar quantum geometry and bipolar quantum superposition Part I – A background independent geometrical and logical exposition of Dirac 3-polarizer experiment. Fractal Geometry and Nonlinear Anal in Med and Biol 1.
- Zhang WR (2011) YinYang Bipolar Relativity: A Unifying Theory of Nature, Agents and Causality with Applications in Quantum Computing, Cognitive Informatics and Life Sciences. IGI Global, Hershey and New York, 2011.
- Zhang WR, Zhang L (2004) YinYang Bipolar Logic and Bipolar Fuzzy Logic. Information Sciences 165: 265-287.
- Zhang WR, Pandurangi A, Peace K (2007) YinYang Dynamic Neurobiological Modeling and Diagnostic Analysis of Major Depression and Bipolar Disorder. IEEE Trans on Biomedical Engineering54:1729-39. [Crossref]
- Zhang WR, Zhang HJ, Shi Y, Chen SS (2009) Bipolar Linear Algebra and YinYang-N-Element Cellular Networks for Equilibrium-Based Biosystem Simulation and Regulation. J of Biological Systems17: 547-576.
- Dirac P (1930)The principle of Quantum Mechanics. Oxford University Press Inc., (4th Edn), New York, Reprinted 2004.
- Mandelbrot B (1982) The Fractal Geometry of Nature, W H Freeman & Co, 1982.
- Smolin L (2005) The case for background independence. Jul 2005.
- Einstein A (1940) Considerations Concerning the Fundaments of Theoretical Physics. Science91: 487-492. [Crossref]
- Avnir D, Biham O, Lidar D, Malcai O (1998) Is the Geometry of Nature Fractal? Science 279: 39-40.
- Einstein A, Podolsky B, Rosen, N (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 47: 777-780.
- Zhang WR (2007)YinYang bipolar universal modus ponens (bump) – a fundamental law of non-linear brain dynamics for emotional intelligence and mental health. Walter J. Freeman Workshop on Nonlinear Brain Dynamics, Proc. of the 10th Joint Conf. of Information Sciences, Salt Lake City, Utah, USA, July 2007, 89-95.
- Zhang WR (2003a) Equilibrium Relations and Bipolar Cognitive Mapping for Online Analytical Processing with Applications in International Relations and Strategic Decision Support. IEEE Trans on SMC Part B 33: 295-307. [Crossref]
- Zhang WR (2003b) Equilibrium Energy and Stability Measures for Bipolar Decision and Global Regulation. International Journal of Fuzzy Systems 5: 114-122.
- Zhang WR, Peace KE (2014) Causality Is Logically Definable—Toward an Equilibrium-Based Computing Paradigm of Quantum Agent and Quantum Intelligence (QAQI) (Survey and Research). Journal of Quantum Information Science 4: 227-268.
- Zhang WR (2012a) YinYang Bipolar Atom – An Eastern Road toward Quantum Gravity. J of Modern Physics 3: 1261-1271.
- Zhang WR (2012b) Beyond Spacetime Geometry – The Death of Philosophy and Its Reincarnation. J of Modern Physics 3: 1272-1284.
- Zhang WR (2013) Bipolar Quantum Logic Gates and Quantum Cellular Combinatorics – A Logical Extension to Quantum Entanglement. J of Quantum Information Science3: 93-105.
- Zhang WR, Peace KE (2013) Revealing the Ubiquitous Effects of Quantum Entanglement – Toward a Notion of God Logic. J of Quantum Information Science 3:143-153.
- Schrödinger E (1944) What is life? Cambridge University Press, UK, First Published 1944.
- Gore J, Van Oudenaarden A (2009) Synthetic Biology: The Yin and Yang of Nature. Nature 457: 271-272. [Crossref]
- Shi Y, Seto E, Chang LS, Shenk T (1991) Transcriptional Repression by YY1, a Human GLI-Kruppel-Related Protein, and Relief of Repression by Adenovirus E1A Protein. Cell 67: 377-388. [Crossref]
- Einstein A (1934) On the Method of Theoretical Physics. The Herbert Spencer Lecture, Mein Weltbild, QueridoVerlag, Amsterdam.
- Ball P (2011) Physics of Life: The Dawn of Quantum Biology. Nature 474: 272-274. [Crossref]
- Rosenfeld S (2013) Group consensus theorem and self-organized criticality: unifying principles for understanding self-organization, swarm intelligence and mechanisms of carcinogenesis. Gene Regul Syst Biol 7: 23–39. [Crossref]
- Rosenfeld S (2015) Critical junction: Nonlinear dynamics, swarm intelligence and cancer research.Fractal Geometry and Nonlinear Anal in Med and Biol 1: 7-10. [Crossref]
- Einstein A (1916) The Foundation of the General Theory of Relativity. Annalen der Physik 49: 769-822. [Crossref]
- ‘t Hooft G (2014) The Cellular Automaton Interpretation of Quantum Mechanics: A View on the Quantum Nature of our Universe, Compulsory or Impossible?
- Weinberg S (2011) Collapse of the State Vector, UTTG-18-11, 2011).
- BBC (2006) Negative Numbers. Last broadcast on Thu, 9 Mar 2006, 21:30 on BBC Radio 4.
- Zhang WR,Marchetti F (2015) A Logical Exposition of Dirac 3-Polarizer Experiment and Its Potential Impact on Computational Biology. Proceedings of ACM Conference on Bioinformatics, Computational Biology, and Health Informatics (ACM BCB) – 2015, 517-518.

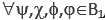
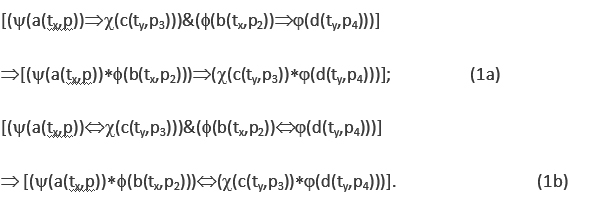
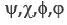 are bipolar predicates; * is a bipolar universal operator that can be bound to any binary operator in BDL; Þ is bipolar implication; a(tx,p), b(ty,p2), c(tx,p3), d(ty,p4) are bipolar quantum agents where a(t,p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in spacetime). An agent p without time and space is assumed at any time t and space p. An agent at time t and space p is therefore more specific.
are bipolar predicates; * is a bipolar universal operator that can be bound to any binary operator in BDL; Þ is bipolar implication; a(tx,p), b(ty,p2), c(tx,p3), d(ty,p4) are bipolar quantum agents where a(t,p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in spacetime). An agent p without time and space is assumed at any time t and space p. An agent at time t and space p is therefore more specific.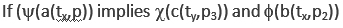 implies
implies 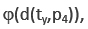 then the bipolar interaction
then the bipolar interaction