Take a look at the Recent articles

Abstract

Many cancers have been characterized by their expression of multiple “driver” oncogenes [1]. This implies a sequence of crucial developmental “decisions” required to implement an oncogenic “program”. Are all or at least most of these decisions deterministic and others “stochastic” in implementation? Certain inborn errors of metabolism and hereditary cancers are largely deterministic. And yet to account for the widespread differences in detail of gene expression within and between cancer cells from different regions of the same cancer, to what extent are these variations at a fine-grained level subject to “decision trees” or “nodes” that may often depend upon stochastic events, engrafted on to more fundamental cell, tissue, organ or unfolding aberrant cancer-oriented deterministic programs [2,3]? Considering that many epithelial cancers develop over a number of years, does an admixture of determinative and stochastic decision-events contribute to a protracted maturation of epithelial cancers? The potential effect of cellular stress such as that due to hypoxia on the outcomes from stochastic events is uncertain.We consider some of these questions, employing a differential – logistic Monte Carlo simulation with continued stochastic input to a fixed carrying capacity, K, of slowly and rapidly proliferating daughter cancer cells as a visual model for this discussion. An Appendix with further details of the programs employed is provided at: www.uic.edu/nursing/publicationsupplements/stochastic Anderson Rubenrstein Guinan Patel.pdf

Key words

oncogene “ decision trees” determinative, stochastic, random

Introduction

It is the case that many genetic and epigenetic events affecting human cancers are considered to occur “stochastically”, as distinguished from those occurring deterministically or randomly [4-8]. From one point of view, for example, that of radiation carcinogenesis, deterministic effects on cells exhibit a threshold and their effects are dose-dependent. The likely outcome of converting some “normal” cells to cancer cells is subject to quantification, but which specific cell will be affected is uncertain. For stochastic processes associated with ionizing radiation, thresholds should not exist, the probability of occurrence depends upon the absorbed dose and the severity of effect is independent of it [9].

A stochastic process can be defined as a system evolving over time that undergoes “chance” fluctuations. A more analytic definition is that of Claude Shannon [10] as summarized by Gleick [11]. Stochastic processes are neither deterministic (the next event can be calculated with certainty) nor random, (the next event is totally “free”). A truly random process does not have predicable properties and while a chaotic system (“deterministic chaos”) does, they can be difficult if not impossible to identify [12]. Randomness is a form of “incomplete information”, essentially inaccessible due an inability to identify the uncontrolled “causes”.

Each stochastic event has an overall probability dependent upon the prior “state” of the system, contingent upon its’ history. In its’ purist form, the variance and mean of a true stochastic process are equal, characteristic of a Poisson distribution [13]. Stochastic circuits can be designed to produce fairly reproducible behavior [5]. Thus the relative probability of occurrence of an event need not be the absolute single defining feature. However, as a first approximation, mentally it seems useful to distribute most deterministic, stochastic and random events along some sort of probability - axis.

Of course no future event is entirely “free”. Its’ position in its’ local universe depends upon its’ history and contingent features (e.g., intrinsic and extrinsic “noise” [6] associated with the context in which it is sited. Single events cannot be directly compared with multiple ones exhibiting overall statistical predictability. The likelihood of an individual radioactive atom decaying is unknown although in bulk, an overall probability (half-life) can be measured. Some extremely rare events that initiated major biological speciation, established rare inborn errors of metabolism or structure or hereditary malignancies affecting a very few families seem to represent examples of uncommon, previously established “random” genetic events maintained within narrowly circumscribed limits.

It has been increasingly observed that human cancers include multiple clones of related but genetically and phenotypically non-identical malignant cells [14-19]. In point of fact, no two cells from the same or different lineages are likely to be truly “identical” when compared at a sufficiently fine-grained level (“genetic mosaicism”) [17,19]. Cancer cells are believed to include specific “Mut driver” mutations and aberrantly expressed “Epi-driver” events involving proto-oncogene and suppressor genes primarily responsible for subverting normal differentiation and directing subsequent development toward abnormally regulated cancer cells [1]. Malignant cells are thought to be accompanied by “progressor” and “passenger” mutations; the latter do not confer any direct or indirect proliferative advantage on members of the clone. The flow of cancer-related- events is often represented as a developing, arborizing, tree-like structure, representing the distribution of genetic and metabolic changes among the numerous “daughter” cancer cells [3]. These changes are due to both altered DNA and to epigenetic changes in nucleic acids and proteins [20]. Important regulatory roles related to elements in the 99 percent of the genome that does not specify the exome cellular structural and enzymatic elements introduce additional levels of regulation [21,22].

Stochastic events are considered essential for the development of malignant processes [3,23], especially as they might influence the protracted nature of the process. Modeling their potential contribution employing a deterministic Monte Carlo simulation that includes a component of stochasticity can provide a general insight as to how these events might interact over time to influence development of somewhat dissimilar developing “oncogenic” programs in genetically related cancer cell clones. What is uncertain is the extent to which metabolic capabilities already resident in the cancer clones contain all the essential elements required for integration into the unfolding cancer developmental program or whether significant improvisations of existing or of new configurations of genetic or epigenetic developments with new capabilities of interacting are required before a subsequent stage in the oncogenic program can be expressed. To what extent could a delay in any of the stochastic improvisations retard the rate at which the cancer develops?

Methodology and characteristics of a model

Currently it is thought that breast cancer can be classified into four major categories of which some 78 percent are intra-ductal adenocarcinomas [24]. As an example we assume an instance in which a breast cancer occurring in a hypothetical patient age 50, involving some definitive initial oncogenic event, potentially followed by a median number of 32 (range ca 20 to 73) additional non-synonymous (a mutation altering the amino acid sequence of a protein) oncogenic decision “events” [1], of which apparently only some may be absolutely essential to initiate and define the cancer. Presumably, over the following years, expression of a limited subset of the 70 or so altered protein coding genes must be expressed in some sort of order, culminating in a cancer containing 10⁹ or more cells. A mass of cells that size should be detectable by physical examination and half that number (10⁹ / 2) cells by X-ray.

To portray the background for representing and discussing some of these questions, we employed a Monte Carol simulation [25,26], using a logistic model of rapidly or slowly growing simulated cell proliferation [6,27-29] subject to continued stochastic “noise”. Comments concerning the programs employed and their use can be found at: http://go.uic.edu/OncogeneMutationAppendix

Results

Employing a representative logistic equation and depending upon the parameters chosen, a series of growth curves with a gradually increasing time to appearance (TPA) to the carrying capacity, K was generated. Once K is reached, cells are considered to enter a quiescent phase that precedes their further “history”. With a fixed carrying capacity, K (the number of cells that can proliferate in the local environment), an initial cell (po=I) and an increasing r (the proliferation rate, p–death rate, d) shortened the TPA and the time to achieve 5x10⁴ K; reducing r lengthened it (Figure 1). When K was increased and r held constant, as expected, the TPA increased (not shown). Continuous stochastic simulations, represented by the generation of random numbers, introduced a number of potential “alternative” clonal proliferation histories (Figure 2). A single cell considered to express an initiating “driver” cancer mutation(s), (left plot, slowly growing ( K=50,000; r=0.25) generates multiple notational daughter cells represented by the small squares that lie on, near or further away from the line representing the average behavior of the population over time t. These “cells” and their progeny can be imagined to represent potential clones expressing differences in proliferation rate, especially if above the average and / or other genotypic or phenotypic properties. In the histogram of the error term, et, negative values are ignored; an initial cell was considered to have initiated the proliferation. The frequency of random “events”, cs, and the distribution of random numbers, et both begin to assume the symmetry of a Bell curve. In Figure 3, the stochastic “fast” model (K=50,000, r=7) provides comparable information subject to a different random sequence, since each “cell” is at risk from individual and possibly unique stochastic events.

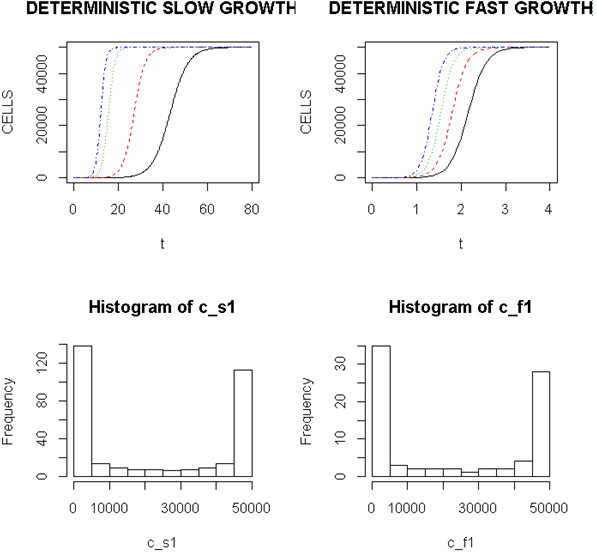
Figure 1. Representative Growth Curves with a Constant Carrying Capacity of 50,000
Left (upper) panel, slow proliferators, r from 0.25, 0.7, 0.9 and 1.0, right to left and right panel, fast proliferators, r from 5.0, 6.0, 7.0 and 8.0, right to left. Abscissa- arbitrary time; ordinate- number of cells

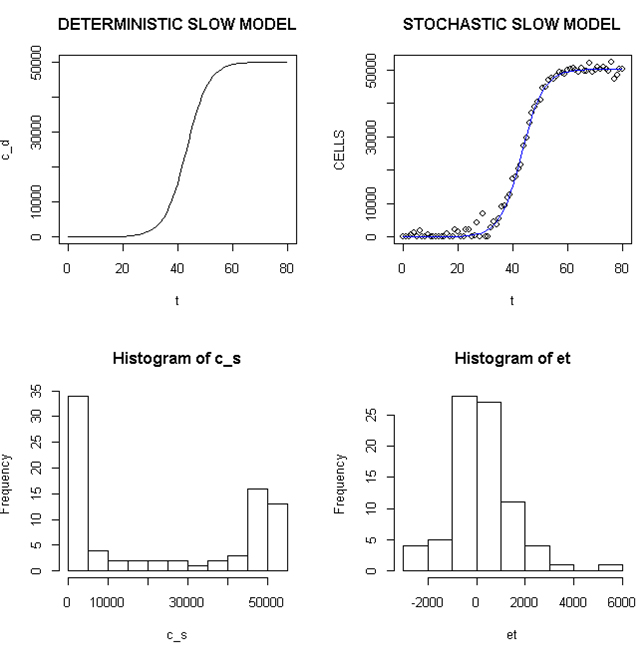
Figure 2. Deterministic and Stochastic Plots of Slowly Proliferating Notational Cells
Upper panels: Carrying capacity of 50,000, r (slow)=0.25; Lower panels: Et (error term) and c_ s: cells in stochastic model.

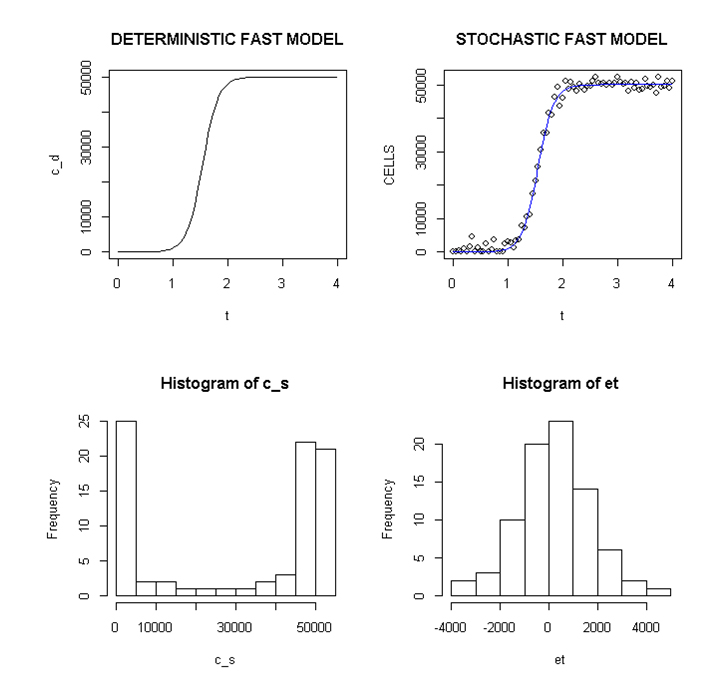
Figure 3. Deterministic and stochastic Plots of Rapidly Proliferating Notational Cells Upper panel: carrying capacity K of 50,000, r=7; Lower panels: ET (error term) and c _ s: cells in stochastic model.

Slowly and rapidly proliferating “cells” at 5000 and 500 values of K were studied with comparable results (not shown). The distribution of these stochastically generated “cells” was more variable and care needs to be taken in choosing parameters to depict them. These programs are presented in the Appendix, accessible on the web with directions for their use. The chief limitation in scalability seems to be the value chosen for the scaleval; a ratio of scaleval / K=0.125 to 0.016 are the values employed in the two programs.

Each stochastic “event” represents some form of “singularity” that may be considered to alter that Individual cells’ history, depending upon the state of the affected cell and its’ ability or inability to respond to the “event”. As the appearance of these singularities depends upon the generation of random numbers, the ordering of the sequences for each cell is unique.

The program of course excludes “negative” cells lying below zero on the Y axis. Initially there is an apparent lack of cells vis a’ vis stochastic “events” and also at the end of the run when K is approached. The early proliferative “events” occur exponentially; later events are terminated according to the logistic equation. Large K values greatly compresses “events” compared with results with smaller K values, affecting scalability by obscuring finer differences apparent with lesser numbers of cells.

Discussion

As a visual representation of the potential contribution of stochastic events in multiple but closely related cancer clones in different regions of a cancer and subject to a continued stochastic history, a modified logistic- proliferative equation [28,29] can be viewed as mimicking aspects of that outcome. It is tempting to interpret the numerous individual paths culminating notationally in some clones differing for example, in apparent proliferative potential. These hypothetical, individual cells would, over time, be exposed to differing forms of intrinsic noise related to specific instances of gene and exome expression, in addition to extrinsic noise from fluctuation of components devoted to other aspects of cellular growth and survival [6,30]. A stochastic “event”, some form of “singularity” occurs that may alter the subsequent fate of that cell, depending upon its’ state, a function of its’ history. An altered proliferation rate or other regulatory or metabolic changes in individual “cells” related to stochastically generated genetic / epigenetic differences may be responsible.

Stochastic events can be identified by fluorescence, including fluorescence in situ hybridization (FISH) to measure proteins or multiple mRNAs or by quantitative single cell RT-PCR to distinguish between intrinsic and extrinsic “noise” [6]. If different genes in a cell respond in the same direction, that is consistent with a response to extrinsic noise [6]. In one early study, two copies of the same promotor were introduced into E. coli, one detected by a cyan fluorescent protein, the other by a yellow fluorescent protein [30]. Extrinsic noise was considered to affect both promotors in a correlated response, due to details of ribosomes, polymerases etc. If the promotors responded independently, this intrinsic noise was ascribed to randomness inherent in transcription and translation.

To try and visually simulate this effect we applied sequences of random numbers, taken to represent the occurrence of unknown stochastic events to rapidly and slowly proliferating “cells”. Each individual event would be unique to that cell and no two cells would present identical intracellular environments in response to a stochastic “event.” Cells with unique histories would also be exposed individually to different stochastic events at differing times. Slowly and rapidly proliferating cells, representing different metabolic and phenotypic environments, could be expected to respond or not differently to random intrinsic and possibly extrinsic noise. Once rapidly dividing cells reach their K-value, both they and the remaining slowly proliferating cells continue to be at “risk” from stochastic events varying in sequence and kind. To the extent this modulation involved any of the 12 major driver categories and signaling pathways affecting cell survival, fate and genomic integrity [1] or programming that directs differentiation, genetically or phenotypically dissimilar clones should result. This could be especially true of cells subjected to hypoxic or other forms of stress [31-34].

In the C.elegans system it was proposed that in the absence of additional genetic variation, stochastic variation in the abundance or activity of “genetic interaction partners”, defined as genes and their products that influence the outcome of a mutation when genetically altered, determines the expression of the original mutation [35]. The signal transduction pathways that link the expression of an oncogene with downstream stochastic events, some affecting downstream “nodes”, might be delayed in their implementation. Stochastic responses would introduce a form of a “sum over paths” or over “histories” [36] with clones derived from daughter cells exhibiting different genomic / epigenetic outcomes due to dissimilar pre and post stochastic histories.

If a stochastic event increases the rate of proliferation or contributes to some differentiating event resulting in increased drug resistance, vascularity, reduced cell death etc., a clone of cells with augmented malignant properties may evolve, despite their emersion in a much larger number of other daughter cancer cells. Genetic drift involving small numbers of cells tends to favor the emergence of one clone while others become extinct [37]. However given a sufficiently robust positive growth advantage, unfavorable chance events of genetic drift could be and in cancer, apparently are often overcome [14-20]. If the event affected small numbers of regulatory molecules such as those affecting transcription [6], this might also mitigate countervailing effects of genetic drift.

Individual fast and more slowly proliferating cells likely exhibit fine-grained differences in genetic and epigenetic readouts [17,19]. There are several major considerations; over time, the differing stochastic (random number) events themselves and the state of each responding cell as it undergoes its proliferative and subsequent history. An unknown proportion of cells differentiate, become quiescent, senesce while others die from programmed cell death or necrosis. It is unlikely the number of cell divisions in the two categories of proliferation to reach a chosen “K” will be identical. The “sum over time” or “sum over histories” [36] of proliferative and developmental events for each cell will differ; at any moment no two cells at a fine-grained level are likely to be genetically or metabolically “identical” [31]. Cells undergoing extensive genetic changes of stress from, for example, hypoxia, expose additional genetic or other “targets” to stochastic effects superimposed on these programmed changes. In addition, the kinetic behavior of the different rates of proliferation further ensures that individual histories of their cells differ both within and between these categories.

There is a crude analogy to be made between molecules of water in a wave and the cancer cells in a population. No two individual elements of either population are in a fundament sense “identical” to their neighbors, either in internal components related to structure, function or external location or motion. Yet despite differences in detail, many related to intrinsic properties and antecedent history, chance stochastic events of internal and external “noise” and infrequently, much more rare (random) fundamental alteration in their “developmental” histories, an overall determinative outcome; wave reaches shore, cancer cells proliferate, occurs.

As examples of potential contributions to “noise”, the frequent single nucleotide and copy number differences found in single cells [38,39] and studies of single mammalian cells demonstrating widespread (12 to 24 percent) random mono-allelic gene expression could contribute to the stochastic genotypic and phenotypic differences during cellular proliferation [38]. These alleles were expressed independently and stochastically.

If malignantly transformed cells and their progeny are subject to a series of essential cancer-related “decision trees”, a series of developmental “nodes” expressed over 10 to 20 years, clones that differ to some extent in genetic or epigenetic expression are inevitable. Hypoxic cancer cells represent one category of malignantly transformed, stressed cells [31-34,40,41] that present altered intracellular environments at risk for stochastic effects. Hypoxic cancer cells exhibit an aggressive phenotype, resistance to therapy, are prone to metastasize, contributing to poor patient survival [31]. Hypoxic cancer cells and hypoxia-induced factors HIF 1a, 2a and 3 alter the expression of at least several hundred genes and gene products, providing an altered genetic environment to respond to any stochastic incidents, and a stem cell- like phenotype associated with an epithelial to mesenchymal transition [31,33,40,41]. Metabolic changes include reduced oxidative phosphorylation, increased anaerobic glycolysis, a switch to glutamine for fatty acid and energy synthesis, increased synthesis of angiogenic factors such as VEGF, resistance to radiation and chemotherapy, and importantly, impaired DNA repair [41] and several other forms of genomic instability. While hypoxic cells exhibit significant proliferation, upon re-oxygenation, rates of proliferation increase. Hypoxic and other stressed cells and their progeny seem likely candidates to express unexpected responses to intrinsic and extrinsic stochasticity, compared with unstressed normoxic cells. This should contribute to the genomic and phenotypic diversity observed in clinical cancers [19-22]. In a study of gliomas arising from dedifferentiation of normal cells, about half the mutations detected in the original tumors were not found in their metastases [42]. Although much of this diversity is considered due to “passenger” events, retention of essential driver events presumably underwrites the overall oncogenic “program”. A “cross section” of genomic differences among cancer clones in different regions of a tumor subject to the arborization of multiple cell divisions in many potentially distinctive lineages should inevitably include many differences in fine cellular detail.   

Summary

A modified Monte Carlo simulation retaining stochasticiity during simulated cell proliferation can representationally mimic opportunities for potential stochastic effects on cancer cells contributing to their mosaicism. Such putative effects [43] seem even more likely to affect cells under stress such as hypoxia with activation of numerous compensatory genomic events at risk from stochastic events. The time required for transition from one stage of oncogenesis to the next may be influenced by or even depends upon stochastic events, acting upon stressed cell responses contributing to the delay in evolving fully malignant clones capable of metastases.

The “sum-over-paths” or” sum-over- histories” [36], with their interaction of multiple components that reinforce or cancel one another, in some ways resembles the random and stochastic generation of outcomes underlying the contingent evolution of biological life.

Acknowledgments

We thank the Seidel Family Trust and Dr. Jules Harris for their support. Thanks are also due to Dr. George Dunea, Director of the Hektoen Institute and to Dr. Peter Hart, Direct of the Renal Division and his staff at the Cook County Hospital, Chicago, Illinois for their continued support. We also thank Kevin Grandfield for his editorial assistance.

References

1. Vogelstein B, Papadopoulos N, Velculescu VE, Zhou S, Diaz LA Jr, et al. (2013) Cancer genome landscapes. Science 339: 1546-1558. [Crossref]
2. Gilbert SF (2006) The genetic core of development, 77-99; The paradigm of differential genetic expression, 101-138, Medical implications of developmental biology, 655-689 in Developmental Biology, Sinauer Assoc. Inc, Sunderland, MA.
3. Weinberg RA (2007) Maintenance of genomic integrity and the development of cancer, 463-526; The rational treatment of cancer, 725-795 in The Biology of Cancer, Garland Science, Taylor and Francis Group, NY.
4. Till JE, Mc Culloch EA, Siminovitch L (1964) A stochastic model of stem cell proliferation, based on the growth of spleen colony-forming cells. Proc Natl Acad Sci U S A 51: 29-36. [Crossref]
5. Scott M, Hwa T, Ingalls B (2007) Deterministic characterization of stochastic genetic circuits. Proc Natl Acad Sci U S A 104: 7402-7407. [Crossref]
6. Raj A, van Oudenaarden A (2008) Natu2021 Copyright OAT. All rights reservne expression and its consequences. Cell 135: 216-226. [Crossref]
7. Shmulevich I, Aitchison JD (2009) Deterministic and stochastic models of genetic regulatory networks. Methods Enzymol 467: 335-356. [Crossref]
8. Keener J, Sneyd J (2009) Appendix. Stochastic processes, 103-114, in Mathematical Physiology I: Cellular Physiology. 2^nd edn; Springer, NY.
9. Hall EJ (1998) Late effects of radiation: Carcinogenesis and nonspecific life shortening, 385-409; Late effects of radiation: genetic changes, 413-426 in Radiobiology for the Radiologist; JB Lippincott, Philadelphia.
10. Shannon CE, Weaver A (1949) The Mathematical theory of Communication; U of IL Press, Urbana, IL.
11. Gleich J (2011) The Information; Pantheon Books, NY: 225.
12. Taleb NN (2007) The Black Swan; Random House, NY: 197-198.
13. Spiegel MR, Stephens LJ (1999) Theory and Problems of Statistics (3^rd Edn); 158.Schaum’s Outline Series, NY.
14. Yachida S, Jones S, Bozic I, Antal T, Leary R, et al. (2010) Distant metastasis occurs late during the genetic evolution of pancreatic cancer. Nature 467: 1114-1117. [Crossref]
15. Stratton MR (2011) Exploring the genomes of cancer cells: progress and promise. Science 331: 1553-1558. [Crossref]
16. Li M, Wang IX, Li Y, Bruzel A, Richards AL, et al. (2011) Widespread RNA and DNA sequence differences in the human transcriptome. Science 333: 53-58. [Crossref]
17. Shibata D (2012) Cancer. Heterogeneity and tumor history. Science 336: 304-305. [Crossref]
18. Gerlinger M, Rowan AJ, Horswell S, Larkin J, Endesfelder D, et al. (2012) Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. N Engl J Med 366: 883-892. [Crossref]
19. Lupski JR (2013) Genetics. Genome mosaicism--one human, multiple genomes. Science 341: 358-359. [Crossref]
20. Suvà ML, Riggi N, Bernstein BE (2013) Epigenetic reprogramming in cancer. Science 339: 1567-1570. [Crossref]
21. Pennisi E (2012) Genomics. ENCODE project writes eulogy for junk DNA. Science 337: 1159, 1161. [Crossref]
22. Kentwell J, Gundara JS, Sidhu SB (2014) Noncoding RNAs in endocrine malignancy. Oncologist 19: 483-491. [Crossref]
23. Odoux C, Fohrer H, Hoppo T, Guzik L, Stolz DB, et al. (2008) A stochastic model for cancer stem cell origin in metastatic colon cancer. Cancer Res 68: 6932-6941. [Crossref]
24. Ma CX, Ellis MJ (2013) The Cancer Genome Atlas: clinical applications for breast cancer. Oncology (Williston Park) 27: 1263-1269, 1274-9. [Crossref]
25. Tenekedjiev KI, Nikolova ND, Kolev K (2011) Applications of Monte Carlo Simulation in Modelling of Biochemical Processes. [doi: 10.5772/14984].
26. Tuckwell W, Bezak E, Yeoh E, Marcu L (2008) Efficient Monte Carlo modelling of individual tumour cell propagation for hypoxic head and neck cancer. Phys Med Biol 53: 4489-4507. [Crossref]
27. Andrecut M (2004) Monte-Carlo simulation of a multi-dimensional switch-like model of stem cell differentiation. J Mol Histo 35: 667-677. [doi: 10.5772/14984].
28. Lawless C (2012) A discrete, stochastic, logistic population model. Swiss net discrete stochasticlogistic.
29. Volz E, Meyers LA (2007) Susceptible-infected-recovered epidemics in dynamic contact networks. Proc Biol Sci 274: 2925-2933. [Crossref]
30. Elowitz MB, Levine AJ, Siggia ED, Swain PS (2002) Stochastic gene expression in a single cell. Science 297: 1183-1186. [Crossref]
31. Semenza GL (2013) HIF-1 mediates metabolic responses to intratumoral hypoxia and oncogenic mutations. J Clin Invest 123: 3664-3671. [Crossref]
32. Yuen A, Diaz B (2014) The impact of hypoxia in pancreatic cancer invasion and metastases. Hypoxia 2: 91-106.
33. Ma Y, Liang D, Liu J, Axcrona K, Kvalheim G, et al. (2011) Prostate cancer cell lines under hypoxia exhibit greater stem-like properties. PLoS One 6: e29170. [Crossref]
34. Tiburcio PD, Choi H, Huang LE (2014) Complex role of HIF in cancer: the known, the unknown and the unexpected. Hypoxia 2: 59-70.
35. Burga A, Casanueva MO, Lehner B (2011) Predicting mutation outcome from early stochastic variation in genetic interaction partners. Nature 480: 250-253. [Crossref]
36. Feynmann R (1985) QED: The strange story of light and matter. Princeton U Press, NJ.
37. Geiffiths AJF, Wessler SR, Lewontin RC, Gelbart WM, Suzuki DT, et al. (2005) Introduction to Genetic Analysis (8^th edn) 636-637, WH Freeman, NY.
38. Zong C, Lu S, Chapman AR, Xie XS (2012) Genome-wide detection of single-nucleotide and copy-number variations of a single human cell. Science 338: 1622-1626. [Crossref]
39. Deng Q, Ramsköld D, Reinius B, Sandberg R (2014) Single-cell RNA-seq reveals dynamic, random monoallelic gene expression in mammalian cells. Science 343: 193-196. [Crossref]
40. Heddleston JM, Li Z, Lathia JD, Bao S, Hjelmeland AB, et al. (2010) Hypoxia inducible factors in cancer stem cells. Br J Cancer 102: 789-795. [Crossref]
41. Pires IM, Bencokova Z, Milani M, Folkes LK, Li JL, et al. (2010) Effects of acute versus chronic hypoxia on DNA damage responses and genomic instability. Cancer Res 70: 925-935. [Crossref]
42. Friedmann-Morvinski D, Bushong EA, Ke E, Soda Y, Marumoto T, et al. (2012) Dedifferentiation of neurons and astrocytes by oncogenes can induce gliomas in mice. Science 338: 1080-1084. [Crossref]
43. Macneil LT, Walhout AJ (2011) Gene regulatory networks and the role of robustness and stochasticity in the control of gene expression. Genome Res 21: 645-657. [Crossref]
44. Matloff N (2011) The Artof Programing. No Starch Press, San Francisco.