The objectives: Study the blood flow in aorta with the MRI and CT and express initial factors of atherosclerosis.
Methods: Peak velocity, net flow and flow acceleration has been investigated at different sites of aorta in 17 healthy volunteers (18-52y). Blood radiodensity (HU) was measured by the CT scanner.
Results: Blood flow acceleration in initial diastole, at the outer curvature of isthmus, is 11.6 ± 0.6 times higher than that in systole. Net flow from systole to diastole increases 2.5 ± 0.5 times. At the outer curvature of isthmus, from the end of the systole to the initial of diastole, frequency of flow oscillation increases from 0.8Hz to 1.6Hz. Flow separation is more expressed here. Blood density (in HU) in the ascending aorta is 57.3 ± 3.5, at the terminal site of thoracic aorta 25.7 ± 3.1.
Conclusion: At the outer curvature of aortic isthmus, pulse pressure after the reflection is in resonance with the end systolic pressure drop. Amplitude of stress and frequency of oscillation in the boundary layer increases. Flow separates. Frequency dispersion destroys the flow cell aggregates, increasing blood entropy, whereas at the vessel wall, denudates endothelial sheet.
shear stress, boundary layer, viscoelasticity, wave reflection, resonance, frequency dispersion
Atherosclerosis is a leading cause of mortality and morbidity in the western world. It has been recognized for over a century, and the understanding of its pathogenesis has undergone many changes [1]. Atherosclerosis is no longer a disease attributed mainly to the high lipid content of the body. New insight into the disease pathology has shown it to be a disease of much greater ramifications.
Although the pathobiology of atherosclerosis is a complex multifactorial process, blood flow-induced shear stress has emerged as an essential feature of atherogenesis. It is recognized that disturbed or oscillatory flows near arterial bifurcations, branch ostia and curvatures are associated with atheroma formation [2].
Endothelial damage and free radicals have predominantly emerged as factors in virtually all pathways leading to the development of atherosclerosis due to hyperlipidemia, diabetes, hypertension or smoking. The disease appears earliest in the aorta, while it appears in the coronary arteries in the second decade and in the cerebral arteries in the third decade.
Experimental and clinical observations have noted that early endothelial injury is more likely to occur in areas of blood flow separation and low shear stress. These areas tend to occur at the outer walls of arterial branch points and have been shown to induce endothelial dysfunction [3].
It has long been hypothesized that low wall shear stress and the resultant stagnation of blood permit increased uptake of atherogenic blood particles as a result of increased residence time. Prolonged oscillatory shear stress induces expression of endothelial leukocyte adhesion molecules, which are important in mediating leukocyte localization in the arterial wall [4.5].
Blood flow near the intimae, referred to as the boundary layer, is slower and has more disturbed currents. The deduction of the boundary layer equations was one of the most important advances in fluid dynamics. Using an order of magnitude analysis, the well-known governing Navier-Stokes equations of viscous fluid flow can be greatly simplified within the boundary layer [6.7].
Blood is thixotropic and in circulation it has shear thinning property [8.9]. With the increasing velocity gradient in the blood flow nonlinear properties develop.The viscous component of the complex viscosity becomes the order of the steady flow viscosity at high gradients while the elastic component tends to decrease in inverse proportion to the gradient [10].
Blood flow is pulsating. Pulse pressure with the reflected component and to some extent arterial stiffness, is a well-known risk factor for atherosclerosis [11]. Pressure wave reflection plays a crucial role in the manifestation of the augmentation of systolic pressure [12].
However, blood viscoelastic alterations, in conjunction with the wave propagation, is not yet studied. An explanatory mechanism for this association has begun to evolve. MR, CT imaging can be used to confirm, in vivo, what is known from in vitro hemodynamic studies and observations of blood stress oscillations in experimental models. Someday, this may help us better understand the importance of blood flow physiology in the multifactorial etiology of atherosclerosis.
In 17 healthy volunteer (18-52y) peak velocity, net flow and flow acceleration has been investigated at different sites of the aorta, by PC MR Angiography with breath hold, ECG triggering. Blood radiodensity (HU) was measured by the CT scanner.
Pulse rate was 72-78 per minute. Systolic pressure was 115 ± 15 mmHg, Diastolic - 70 ± 10 mmHg. MRA with the flow quantification was carried out. Regional flow parameters were calculated at inner and outer curvature of the ascending aorta, aortic arch and thoracic aorta. 1 mm MR slices in 0.7 cm2 circle area (Figure 1).
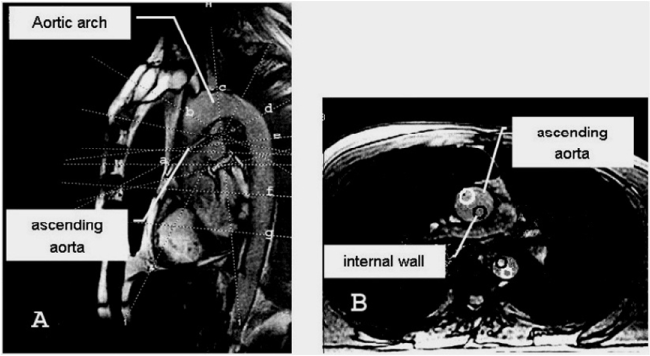
Figure 1. Sites of measurement of the blood flow in the aorta. Dotted lines indicate slices at different walls of the aorta: a-b: ascending aorta, c: aortic arch, d-e: isthmus area, f-g: thoracic aorta. (Dark circle-inner curvature). Sagital view-A, axial view-B.
During systole flow separation is expressed in all sites of aorta. During the initial dyastole, flow acceleration at the outer curvature of aortic isthmus is 11.6 ± 0.6 times higher than that in systole. Net flow from systole to diastole increases 2,5 ± 0.5 folds. From the end of the systole to the initial diastole, at the outer curvature of isthmus, wave oscillation frequencies change from -0.8Hz to 1.6Hz. Blood radiodensity, from the ascending aorta to the terminal part of thoracic aorta, equals to 57.3 ± 3.5H and 25.7 ± 3.1H. (Figures 2 and 3, Table 1).
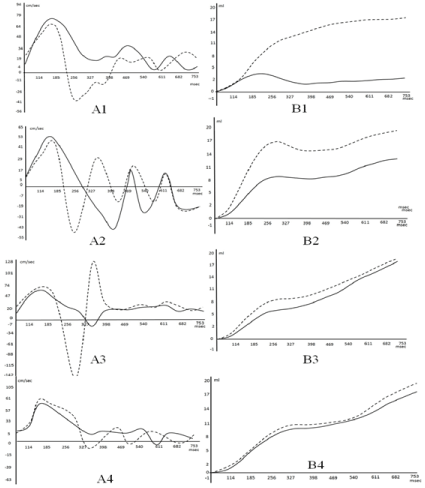
Figure 2.
Peak velocity of blood flow A, and net flow B. at the: 1-ascending aorta, 2-Aortic arch 3. Isthmus of aorta. 4. Thoracic aorta.(P˂0. 05).
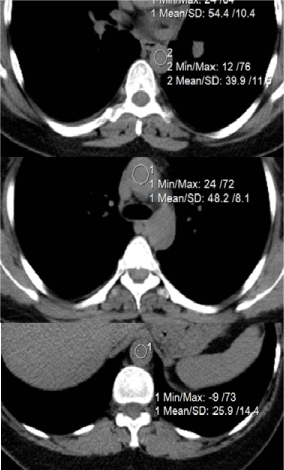
Figure 3. Measurenemt of the blood radiodensity (HU) in different sites of aorta (decreases distally).
Table 1. Peak flow velocity and acceleration in different sites of the aorta.
Measurement site |
Peak velocity (cm/s) in systole |
Flow acceleration (cm/s2) in systole (bold) and from the end systole to initial diastole (underline) |
external curvature |
inner
curvature |
Outer curvature |
inner
curvature |
Entrance of the ascending aorta |
80.3 ± 2.1
|
71.7 ± 1.7 |
422.7-445.4 |
378.4-396.7
|
Aortic arch |
47.8 ± 1.4
|
59.3 ± 1.8
|
227.0-265.9
857.3-944.5 |
310.8-330.3
|
Isthmus area |
60.1 ± 1.2
|
74.7 ± 2.5
|
318.4-331.4
3657,2-3865.3 |
390.3-417.3
571.4-685.7 |
Terminal thoracic aorta |
62.6 ± 2.4
|
59.9 ± 2.7
|
325.4-351.4
330.3-354.7 |
309.2-338.4
|
Aascending aorta (1). (Dotted line ― flow near to outer curvature). Blood flow velocity near to the outer curvature is lower, than that near the inner one. On the peak velocity graph, separated streams flow in opposite directions. Net flow increases at the end of the diastole.
Aortic arch (2). Standing waves arise near to the outer curvature. The resulting waveform is determined by the phase sum of forward and reflected waves. On the net flow graph from the end of the systole to the initial diastole there is a plateau.
Isthmus of the aorta (3). From 185msec, blood flow separates into the opposite directed streams. At 327 msec. waves form the nodule. In the initial diastole peak velocity near outer curvature is sharply increased and becomes higher than that in systole. Net flow increases at the end of the diastole, while from the end of the systole to the initial diastole there is a plateau.
Terminal part of thoracic aorta (4). Wave at 327 msec. forms the nodule. Flow at the different walls is equalized.
The biologic response of the endothelium to hemodynamic forces is important in atherosclerosis. During development of arterial diseases, it is significant to investigate “altered” flow conditions at the boundary layer. In fluid mechanics, a boundary layer is the layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in details [13]. The boundary layer distorts surrounding non-viscous flow. This effect is related to the Womersley’s number.
As a result of their unique location, endothelial cells experience three primary mechanical forces: pressure, created by the hydrostatic forces of blood within the blood vessel; circumferential stretch or tension, created as a result of defined intercellular connections between the endothelial cells; and wall shear stress (WSS), the dragging frictional force created by blood flow. Of these forces, shear stress appears to be a particularly important hemodynamic force because it stimulates the release of vasoactive substances and changes gene expression, cell metabolism, and cell morphology [14]. At the WSS up to the 40 N/m2 causes the endothelial lining of the arterial wall to become disrupted. However, according to the references, the WSS in blood vessels is much below the specified level.
Measurements of WSS in aorta are consistent with the hypothesis that low WSS contributes importantly to conditions that favor atherogenic transformation, but the localization of the plaque, sometimes are different. The convex side of the aortic arch exhibits, relatively to the concave side, high WSS values. High WSS is encountered at the convex side of the end ascending and early descending aorta at all pulse wave times. Particular low WSS values appear along the concave parts of the ascending-descending aorta at regions located just downstream to the left subclavian artery.
It is specified that in the presence of a completely advanced stream of liquid in a straight pipe with the diameter-
d, amplitude of wave fluctuations of velocity-v, viscosity of blood μ and at the flow frequency parameter (Womersley) α, the amplitude of fluctuations of the WSS is:
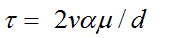 (1)
(1)
According to our data, at the external curvature of the ascending aorta d = 0.025 m, peak systolic velocity vsys= 0.84 m/s, α = 20, μ = 0.004 N.s/m2, and the peak value of the systolic WSS equals to τsys = 5.38 N/m2. At the external curvature of the central aortic arch the peak systolic velocity vsys = 0.48 m/s,τsys = 3.07 N/m2. If you take into account that the diameter of the separate stream is at least 2 times smaller than the aortic diameter, then the WSS in initial diastole becomes two times higher. Systolic peak velocity at the external curvature of the isthmus vsys = 0.60 m/s, τsys = 3.85 N/m2, while at the same place at the initial diastole with the flow separation, peak distolic velocity vdias = 1.42 m/s. and τdias = 18.18 N/m2.
The wave nature of pressure and flow in the arteries has long been recognized. Although the physics of pulse wave propagation and reflection is well understood, it is not clear how reflections contribute to arterial load, or how they affect blood pressure and flow in the dynamically coupled heart-arterial system.
At the boundary layer, pulsating blood flow adjacent to the vessel wall, is affected by perpendicularly directed forces oscillating sinusoidaly with the different phases: axially directed component of the circumferential force (longitudinal wave), and phase delayed radial directed component (transversal wave). On the boundary layer they form the rotating surface wave (Figure 4).
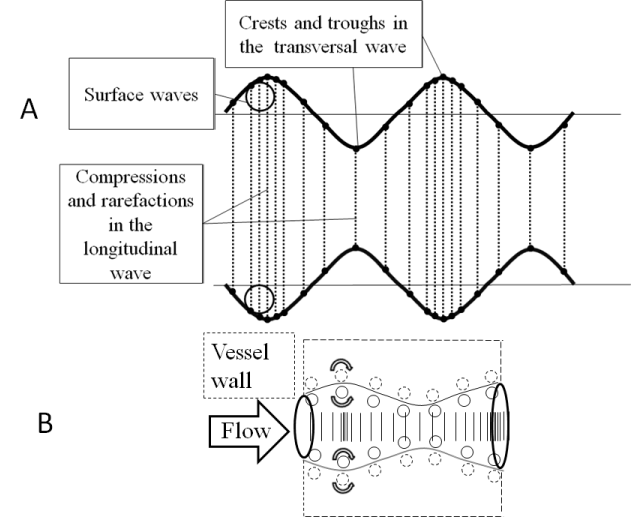
Figure 4. (a) Correlation between longitudinal and transverse waves. Longitudinal wave is made up of compressions and rarefaction,transverse wave is made up of crests and troughs.(b) Surface wave formation at the boundary layer.
If two perpendicular waves have the same oscillation frequency (ω) and are in same phase(φ), than all points the x-value has will be same as the y-value, the output will be a straight diagonal line y-x. If the two waves have exactly the same frequency, but out of synch by φ =π/2, than one of the waves will be like a cosine and resultant output will be a circle (or ellipse if the amplitude of signals are different). The appearance of the figure is highly sensitive to the ratio ω1/ω2. For a ratio 2, and phase difference φ =π/2, the Lissajous figure is like - ∞ (Figure 5).
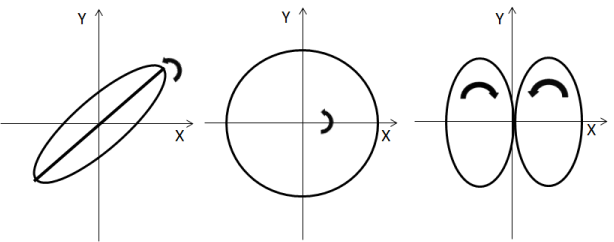
Figure 5. Surface wave motion at the boundary.
Arterial pressure drops sharply in the end of systole and the negative pressure propagates distally. For the waves with equal amplitude and opposite direction, in average there is no net propagation of energy. There is formation of standing wave. From the end of the systole to the initial diastole it is expressed as the plateau on the net flow graph. Standing waves are always associated with resonance and they can be identified by increase in amplitude of the resultant vibrations [15]. On the outer curvature of the isthmus, pressure drop in the end of the systole is in phase with the reflected systolic pulse. Amplitude of the pulse pressure and flow velocity increases.
Oscillation frequency of the elastic string is associated with the tension. At the end of systole, at outer curvature of aortic isthmus, amplitude (high flow acceleration due to the increased stress) and oscillation frequency in the reflected flow wave is higher, than that in incidental one. Flow separates due to the frequency dispersion Figure 6.
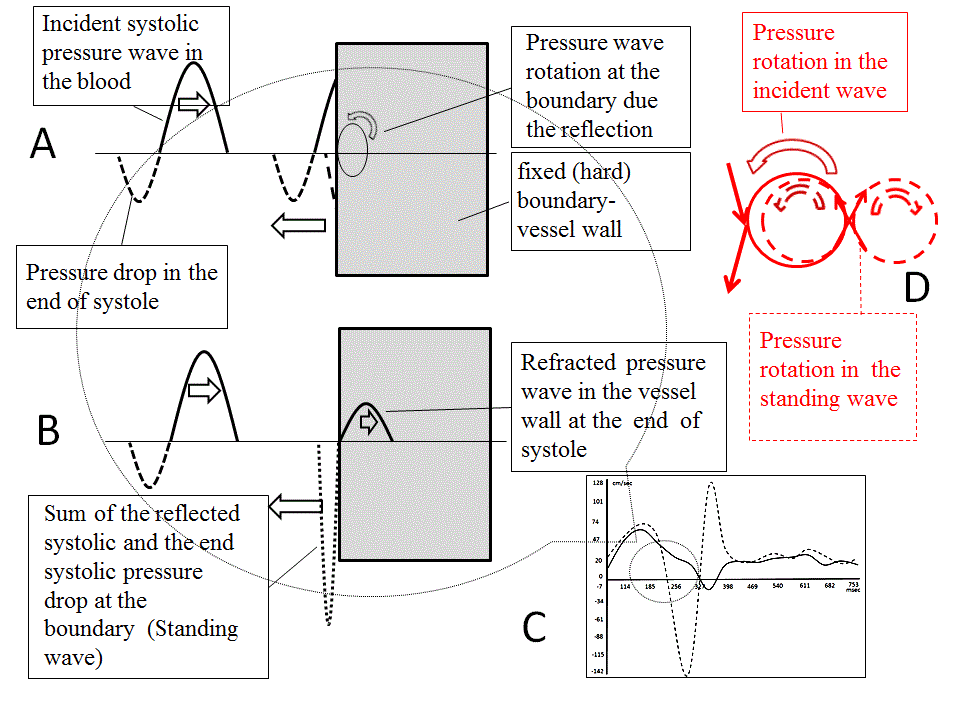
Figure 6. Flow quantification by the Magnetic resonance angiography. Blood flow at the aortic isthmus. In the stream near the outer curvature, amplitude and frequency of the reflected wave is higher, than that in incidental one. In the stream near the inner curvature, wave oscillation frequency stays same. (A -D) At the end of systole, pressure drop is coincident with the systolic pressure wave reflection. In aorta Womerslay’s number is high (inertial flow), velocity profile is flat, and flow wave lags behind the pressure wave (phase delay). Due to the wave superposition, stress and oscillation frequency in the boundary layer increases (B). Dashed lines - flow near the external curvature (C). Refracted (transmitted) wave in the vessel wall has the same frequency, as the incidental one. At the same time, nearby particles in the boundary layer have different velocity and direction. Difference in wave frequency, facilitate to the structural disaggregation of the flowing mass, separation of the flow and shearing of the vessel wall. (D).
Damage of the local wall in atherosclerosis can be explained by the wave vector of a plane wave. The wave vector points to the normal direction of the wave surfaces with the constant phase - wave fronts. At the external wall of the isthmus, angle of incidence of wave vector decreases while the energy transmitted to the wall increases Figure 7.
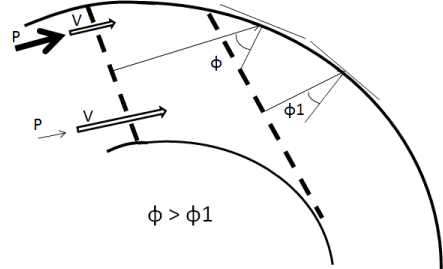
Figure 7. Wave vector is perpendicular to the wave front. At the external wall of the isthmus, angle of incidence (ɸ) of the wave vector decreases and the energy transmitting to the wall increases. Pressure near to the external curvature is higher, than that at the internal one, while the flow velocity is lower. Pressure differences facilitate blood outflow in arterial branches and separation of the flow at the end of the systole.
Motion in the circle, forms pressure gradient towards the radius of the rotation and during the wave reflection, it facilitates the flow separation. It’s same for the aortic arch and arterial branching sites. At the reflection/stagnation point flow velocity is low, while the stress to the wall is high. Due to the turbulence, resistivity in the flow increases and the energy dissipates. Herewith, Womerslay’s number is significantly decreased distal to the high turbulence zones. Turbulence is not chaos, but the method for the distal flow facilitation.
High radio density at the ascending aorta is associated with the erythrocyte aggregation [16]. This phenomenon takes places in normal blood under low-flow conditions. In aggregation and coagulation fibrinogen plays a crucial role. At low shear rates large aggregates lead to an increased viscosity and elasticity, but by increasing the shear rate, the aggregates break up and the viscosity decreases to a constant high shear rate value [17].
From the other hand, at the pressure oscillation, incidental wave at the reflection changes in frequency, while it stay the same for the transmitted wave. Due to the frequence diference in the reflected surface, it destroy red blood cell aggregates, decreases blood viscosity/inertiality, but in the boundary layer it shears the endothelial sheet. It has a relation to the crrep and relaxation of the viscoelastic substance [18]; and represents the main reason for the atherosclerosis.
From the equation (1) at the isthmus of aorta, for the nearby particles at the core of the the different streams, oscillating in different frequences, relative velocity in initial diastole vdias = 1.72 m/s. and the τdias = 22.02 N/m2. Strength limit of the erythrocyte membrane is 5 times higher than that for the endothelial sheet [19]. Due to the turbulence in aortic arch, from the ascending to the end of thoracic aorta blood radio density decreased from 57.3 ± 3.5H to 25.7 ± 3.1H.
It should be presented in some ways to avoid inevitable denudation of the vessel wall:
-In the atherosclerosis, the progressive increase in the bilayer rigidity of cholesterol, parallels the metabolic pathway of sterol biogenesis [20] and may be related to the optimization of visco-elastic properties of vessel wall.
2021 Copyright OAT. All rights reserv
- Flow rate is directly proportional to the gradient pressure. Diastolic pressure is lower than systolic one and net flow in diastole is higher than at the systole. Dynamic viscosity in diastole must be low.
-Pulse rate and position of the heart, due to breath, changes point wave reflection and avoids the continous local damage of vessel.
At the outer curvature of aortic isthmus, pulse pressure after the reflection is in resonance with the end systolic pressure drop. Amplitude of stress and frequency of oscillation in the boundary layer increases. Flow separates. Frequency dispersion destroys the flow cell aggregates, increasing blood entropy, whereas at the vessel wall, denudates endothelial sheet.
- Libby P, Bornfeldt KE, Tall AR (2016) Atherosclerosis: Successes, Surprises, and Future Challenges. Circ Res 118: 531-534. [Crossref]
- McMillan DE (1985) Blood flow and the localization of atherosclerotic plaques. Stroke 16: 582-587. [Crossref]
- Chatzizisis Y, Jonas M, Coskun A, Beige R, Stone B, Maynard C, et al. (2008) Prediction of the Localization of High-Risk Coronary Atherosclerotic Plaques on the Basis of Low Endothelial Shear Stress. Circulation 117: 993-1002.
- Cunningham KS, Gotlieb AI (2005) The role of shear stress in the pathogenesis of atherosclerosis. Lab Invest 85: 9-23. [Crossref]
- [Crossref] Shaaban AM, Duerinckx AJ (2000) Wall shear stress and early atherosclerosis: a review. AJR Am J Roentgenol 174: 1657-1665.
- Day MA (2004) The No-Slip Condition of Fluid Dynamics. Springer: 285-296.
- Wilmer NW, Michael FO and Charalambos VMD (2011) McDonald’s Blood Flow in Arteries: Theoretical. Experimentaland Clinical Principles 755.
- Howard AB (1997) Thiixotropy. Journal of Non-Newtonian Fluid Mechanism 70: 1-33.
- Baskurt OK, Meiselman HJ (2003) Blood rheology and hemodynamics. Semin Thromb Hemost 29: 435-450. [Crossref]
- Thurston GB (1972) Viscoelasticity of human blood. Biophys J 12: 1205-1217. [Crossref]
- Sarah AH, David B, Ian TM and James DC (2005) Waveform Dispersion, Not Reflection, May Be the Major Determinant of Aortic Pressure Wave Morphology. American Journal of Physiology: Heart and Circulatory Physiology 289: 2497-2502.
- Quick CM, Berger DS, Noordergraaf A (2001) Constructive and destructive addition of forward and reflected arterial pulse waves. Am J Physiol Heart Circ Physiol 280: H1519-1527. [Crossref]
- Schlichting H, Gersten K, Krause E and Oertel Jr MC(2004) Boundary-Layer Theory. 8th Edition, Springer, Berlin.
- Davies PF (2009) Hemodynamic shear stress and the endothelium in cardiovascular pathophysiology. Nat Clin Pract Cardiovasc Med 6: 16-26. [Crossref]
- David Halliday, Robert Resnick, Jeral Walker ( 2011) Fundamentals of Physics. JohnWiley & sons.
- Wittram C, Maher MM, Halpern EF, Shepard JA (2005) Attenuation of acute and chronic pulmonary emboli. Radiology 235: 1050-1054. [Crossref]
- Seul Ki, Jeong, Robert S.Rosenson (2013) Shear rate specific blood viscosity and shear stress of carotid artery duplex ultrasonography in patients with lacunar infarction. BMC Neurol V13: 36.
- William N, Findley, James S Lay, Kasif Onaran (2011) Creep and relaxation on nonlinear viscoelastic materials. Dover book
- Timothy J, Pedley (2003) Mathematical modelling of arterial fluid dynamics. Journal of engineering mathematics V47: 419-444.
- Martinez GV, Dykstra EM, Lope-Piedrafita S, Brown MF (2004) Lanosterol and cholesterol-induced variations in bilayer elasticity probed by 2H NMR relaxation. Langmuir 20: 1043-1046.




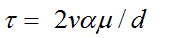 (1)
(1)


