Abstract
The purpose of this study was to investigate the influence of the Ordered Subsets Expectation Maximization (OSEM) reconstruction updates implemented in the 177Lu SPECT/CT imaging processing in molecular radiotherapy. A NEMA IEC Body PhantomTM was used to quantify activity in refillable spheres of five different sizes. Images were obtained with a hybrid dual-head SPECT-CT imaging system (Symbia T2, Siemens Medical System, Germany) with a clinical acquisition protocol, and reconstructed using a commercial 3D OSEM algorithm (Flash 3D). In the reconstruction process, different values of iterations and subsets were considered, along with a 3D Gaussian post-reconstruction filter and scatter and attenuation correction.
Activity recovery coefficients were derived from the ratio between total reconstructed counts and the true activity for each sphere at each OSEM update. Recovery coefficients, and average fractional error (i.e. the weighted Root Mean Squared Error) were evaluated.
At the same time, also 177Lu spatial resolution and dead time were investigated, as matter of discussion about activity recovery coefficients.
Results for spheres ≤ 5.5 ml in volume were significantly affected by the partial volume effect, causing a great bias in activity estimation for the smallest spheres. Their weighted fractional error was OSEM update dependent, ranging between 85% to 79% and 60% to 50% for the two smallest spheres, referring to values of 8 subsets-8 iterations and 16 subsets-10 iterations for the two extremes, respectively. No dead time was detected.
The choice of iterations and subsets is dependent on the object size to investigate and on the desired image quality. Anyway, using a fixed number of iterations and subsets is correct for objects with volumes ≥ 5.5 ml, reaching the total count convergence in the reconstructed volumes, but the use of correction factors for compensating the partial volume effect is needed. For objects with volumes ≤ 5.5 ml the quantification becomes challenging.
Key words
dosimetry, PRRT, Molecular Radiotherapy, OSEM
Introduction
In molecular radiotherapy (MRT) patients with disseminated or unresectable tumors are treated with radiopharmaceuticals that are designed to localize in cancer cells. This approach aims to deliver radiation specifically to tumors, causing minimal toxicity to healthy organs. Neuroendocrine tumors (NET) expressing somatostatin receptors have currently been showing greatly increased incidence, making MRT with 177Lu-labelled somatostatin analogs a promising approach [1,2]. Good clinical evidence has been recently proved in a phase 3 trial for 177Lu Dotatate [3].
Single photon emission computed tomography (SPECT) plays an important role in MRT of NET, since it is at present the main modality used to calculate a patient-specific dosimetry for an accurate and precise MRT planning, as pointed up by the joint EANM / MIRD guidelines for quantitative 177Lu SPECT applied to MRT (MIRD Pamphlet No. 26) [4].
Furthermore, the new EC Directive of 5 December 2013 states that doses to critical tissues must be individually planned and verified for all radiotherapy techniques (including MRT), and requires Member States to introduce legislation enforcing compliance by February 2018. Thus, an accurate personalized MRT planning is required.
The new SPECT/CT systems and their improved quantitative accuracy of 3D imaging allow for a complete and detailed reconstruction of the patient anatomy and a clear localization of the radiotracer uptake area compared to 2D planar imaging [5,6]. Thus, this leads to both localization of tumors, therapy planning, and bio-distribution studies of administered radiopharmaceuticals. The latter information is important for clinicians evaluating to what degree the goal of MRT has been accomplished. In this regard, the need of an accurate SPECT activity quantification within a volume of interest (VOI) represents an important task for the assessment of the therapeutic response, in both clinical and research applications [7-13].
As regards clinical SPECT quantification [14], iterative reconstruction algorithms [15] are the state of the art and they are generally recommended. They are critical in the SPECT/CT image formation chain, and together with target VOIs and quantification protocols, they represent the three main components in activity quantification in SPECT/CT systems. The Ordered Subset Expectation Maximization (OSEM) algorithm [16] is the most widely used among the various iterative reconstruction methods developed to accelerate the reconstruction speed. Several investigations have been reported on the performance of such algorithm on radionuclides frequently used in nuclear medicine, for patient imaging as well as patient specific dosimetry. Some of the more pertinent publications include improvements in correction techniques for quantification in SPECT [4,17-20], evaluations of the accuracy of quantitative image reconstruction techniques [21-25] and comparisons of resolution between SPECT/CT systems using machine-specific reconstruction algorithms [26-28]. In these studies, the OSEM reconstruction parameters (i.e. number of subsets, S, and iterations, I) employed in SPECT image reconstruction are set in order to reach stable values of counts in a variety of considered VOIs.
In the same papers, it is underlined that the imaging characteristics are bounded to: the chosen combination of iterations and subsets, the source distribution, the acquisition counts statistics, the physical degrading effects (scatter, attenuation and collimator-detector response) and are strictly object dependent. Hence, depending on the specific clinical goal (therapy dosimetry rather than diagnostics, for example), it is required to optimize these parameters to obtain the best image quality of reconstructed images, with the aim to perform a reliable quantitative analysis of SPECT images for dosimetry purpose.
In accordance with a recent guidance document issued by European Association of Nuclear Medicine (EANM) [29], the aim of the present study is to find out the optimum combination of the iterations and subsets employed in a commercial OSEM algorithm, in order to establish the quantitative accuracy of our clinical SPECT patient imaging studies. For this purpose, an experimental study was performed using 177Lu-DOTATOC, routinely employed in a clinical trial based on Peptide Receptor Radionuclide Therapy (PRRT) at ASMN hospital in Reggio Emilia, Italy (EUDRACT: 2013-002605-65). The tomographic SPECT phantom images are reconstructed using a commercial 3D OSEM algorithm (Flash 3D, Siemens Medical Solution, Germany), with collimator specific resolution recovery, CT-based attenuation correction and energy window-based scatter correction. The combination of subsets and iterations is evaluated in terms of bias and fractional error. This study is about the influence of the OSEM updates on the SPECT/CT imaging process for therapy purpose. At the same time 177Lu spatial resolution and dead time were investigated.
Materials and methods
SPECT/CT acquisition and reconstruction
SPECT/CT scans were acquired on a Symbia T2 gamma-camera (Siemens Medical System, Germany) with a 3 / 8 inch NaI (Tl) detector and medium-energy low-penetration (MELP) collimator, with a sensitivity of about 13.9 cps/MBq (for ME collimators with 67Ga) extracted from factory data sheet. The tomographic projection images were acquired in step and shoot mode, for 64 views over 360° and 30 sec/frame. Zoom of 1, circular radius of rotation of 330 mm (around the phantom surface) and image matrix of 128x128 pixels were set, resulting in a 4.8 mm pixel size image. In acquisition, the energy windows of the two dominant photopeaks of 177Lu [4] were set at 113keV ± 7.5% and 208.4keV ± 7.5%, as also described in Grassi et al [30]. As regards the lower energy photopeak, the TEW scatter correction was employed and the lower scatter window was set in the range from 87.58keV to 104.53keV (using a default window weight of 0.5), while the upper scatter window from 121.47keV to 130.51keV (using a default window weight of 0.9375). With respect to the higher energy photopeak, the DEW scatter correction was employed and the lower scatter window ranged from 171.60keV to 192.40keV (using a default window weight of 0.75) [30].
Following the SPECT acquisition, an X-ray CT scan of the phantom was generated using a 130kV and 30 mAs beam (clinical parameters), and a smooth reconstruction kernel (B08s; Siemens Medical Solution, Germany). The reconstructed slice thickness was set to 5 mm.
Reconstruction of SPECT / CT images and imaging analysis were performed in Siemens E-Soft workstation (Syngo MI, Application version 32B, Siemens Medical Solution, Germany). The images were reconstructed with the proprietary iterative Flash 3D reconstruction algorithm which includes correction for attenuation (based on energy extrapolation of the CT values from the automatically registered SPECT / CT image), compensation for scatter (estimated by means of the multiple energy windows method, and incorporated into the reconstruction) and a full collimator-detector response [30].
In this study only phantoms were considered. The acquisition set up of the camera is shown in Figure 1.
Iterative reconstruction of the images was performed using a number of iterations ranging from 1 to 20, in steps of two iterations, using 2, 4, 8 and 16 number of subsets. Finally, reconstructed images were filtered with a 3-D Gaussian function having a full width-at-half-maximum of 1 pixel (4.8 mm) [22].
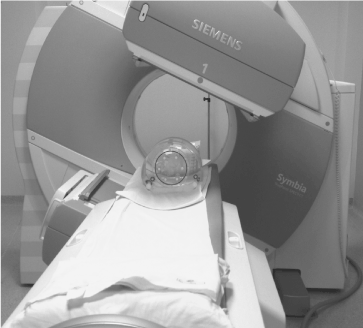
Figure 1. Acquisition set-up where the six radioactive spheres into the NEMA IEC Body PhantomTM are acquired in the SPECT/CT imaging system.
Phantoms
The dead time effect of detectors was investigated with a cylindrical phantom provided with some spherical inserts (internal volume 5640ml) supplied by Data Spectrum Corporation (Hillsborough, USA). It was provided with a set of 6 hollow spheres (in volume of 98, 27, 19, 11.5, 5.6, 2.57 ml), which were filled with a radioactive solution of 177Lu (3,44 MBq/ml that is: 337, 93, 65, 40, 19, 9 MBq respectively) and placed in a radioactive background (0,38 MBq/ml). This phantom was acquired several times while decaying (for about 3.5 half-lives). For each sphere a spherical VOI was drawn directly on its CT image relative to a different time point and the total counts were analyzed in function of time after phantom preparation. Similarly, the total body reconstructed counts were plotted in function of the true activity injected in the phantom.
To test the 177Lu system’s tomographic spatial resolution of the gamma camera, an additional phantom was prepared. It was a cylindrical phantom in which three capillary tubes (length 75 mm, internal diameter 1.2 mm) filled with a radioactive solution were firmly placed: a tube was fixed in central position, while the remaining two tubes were placed at a distance of 3 cm and 6 cm from the central position, even though not on the same axis. Each capillary tube was totally filled with an activity of 30 MBq of 177Lu. For different OSEM updates, the spatial resolution was evaluated as the average of FWHM (Full Width at Half Maximum) values on three counting profiles across each capillary tube.
To study the impact of the reconstruction algorithm updates on the quantification, the NEMA IEC Body PhantomTM (Data Spectrum Corporation, Hillsborough, NC, USA), originally designed for PET scanners, was used. It consisted of a body shaped water-filled cavity, within which five fillable spherical inserts of volume 22.46, 11.46, 5.56, 2.56 and 1.15 ml were fixed on plastic rods that utilized the pre-drilled-and-tapped holes of the phantom. All the spheres were filled with a 177Lu-water solution and were measured one-by-one in a dose calibrator: activity concentrations ranged between 7.5 and 8.8 MBq/ml and these values were used to normalize the following data analysis. The background volume of the phantom cavity was 9.71 liters and it was filled with non-radioactive water.
Whilst for PET applications NEMA recommends leaving the 2 largest spheres cold, for SPECT applications all spheres were filled with radioactivity (choice driven by the inferior system spatial resolution when compared to PET).
Data analysis
Each reconstructed image was analyzed by means of the volumetric analysis tool on the processing workstation supplied by Siemens. For each sphere inside the phantom, its central plane was determined visually and a spherical VOI (generated with a fixed diameter based on the central position and as large as the real spheres diameter) was drawn on the CT image to match the geometric size of the interior of each sphere. Then, the SPECT image was superimposed on the CT and the total reconstructed counts (Cm), mean (Cmean) and also the standard deviation (Cstd) of pixel counts were recorded. To minimize the spill out of recorded counts from the sphere region and spill in from neighboring spheres (because of the initial manual positioning of the VOI), and to optimize the residual misregistration of SPECT and CT images, each VOI was manually shifted by one voxel in negative and positive x, y and z direction. Then, for each combination of iterations and subsets considered, it was possible to calculate a mean value of the measured data.
In absence of partial volume effect, it is possible to define a calibration factor with the general equation [31]:
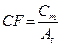 (1)
(1)
where the value of Cm and At refers to the measured counts and true activity values in the region of interest. It was calculated for our SPECT/CT scanner and shown in Grassi et al. [30].
Anyway, for smaller objects, affected by partial volume effect (PVE), it is needed to consider a recovery coefficient (RC) factor, defined as a function of sphere volume as [31]:
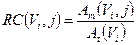 (2)
(2)
where Am(Vi,j) is the reconstructed activity, obtained by the CF value, of the i-th sphere of volume Vi for the particular combination (j) of OSEM update, and At(Vi) is the true activity for the same i-th sphere. At(Vi) was decay corrected as follows [30]:
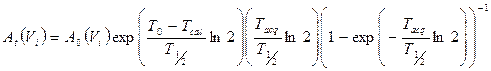 (3)
(3)
where A0 is the initial activity in the sphere volume (Vi), T0 the acquisition start time, Tcal the time of activity calibration, T1/2 the half-life of 177Lu and Tacq is the acquisition time. The first term in brackets corrects for the radioactive decay from the time of calibration to the acquisition start time. The second term corrects for the acquisition time, while the third term calculates the mean counts considering an exponential decay during acquisition, Here, the A0 for each sphere was determined by a direct measurement in a dose calibrator.
From the data obtained by the previous equations, we computed the root mean square error (RMSE) for the activity of each sphere as [28]:
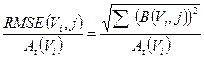 (4)
(4)
where B(Vi,j) is the bias in activity estimation defined as:
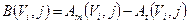 (5)
(5)
computed for the i-th sphere of volume Vi and for the OSEM updates considered. The average fractional error in activity estimation over all spheres (i.e. the weighted RMSE, wRMSE) is, calculated as:
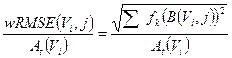 (6)
(6)
Here, k refers to the product of subsets and iterations (i.e. equivalent iteration, EI=S · I) set in the reconstructed images, and fk is its weighting factor.
Results
In Figure 2 the results relative to the dead time effect of detectors are plotted as total reconstructed counts measured on the phantom image versus the true total activity injected in the phantom (linear regression with R2=0.99). No dead time effect was detected. In addition, the physical half-time for the spheres was tested through just as many exponential decay fitting curves and it was perfectly conserved (error within 1% and average R^2 = 0.99).
In Table 1 the estimated tomographic spatial resolution is reported for different numbers of subsets and iterations (from 4 to 16 subsets and from 4 to 18 iterations respectively).
In order to establish the relationship between the choice of OSEM parameters and partial volume effects on recovered concentrations in SPECT reconstruction, we have measured the change in total counts inside each sphere as a function of increasing iterations and subsets. The results are shown in Figure 3a-e. The value of each data point is obtained as the mean of the six VOI drawn on each sphere. As can be seen for the largest spheres, the graphs (Figure 3 a, b, c) show a curve shape of a typical convergence: a fast increase followed by a slower approach towards an asymptote, in accordance with the OSEM object-dependent convergence properties [32]. It has been seen that with the increase of target volumes, it is required a higher number of subsets to reach total counts convergence more quickly, along with a decrease in the variation among different realizations. The last result is different for the case of smaller spheres (Figure 3 d, e), where the total reconstructed counts are quite diverse and they increase for higher updates without reaching convergence even for a great number of iterations (> 20, results not shown). As can be deduced from the same graphs, 8 iterations and subsets ≥ 4 seem to be considered a starting point for total counts convergence, with exception of smaller spheres where greater number of subsets has to be considered.
The results obtained for the computation of the RC, stated in equation (2), are shown in Figure 4. Here, the plots of the calculated RC are shown as a function of the whole reconstruction parameters used in the study for each sphere. The plots provide information of the PVE relative to a reconstructed image of a sphere of a given diameter, and also allows for the lack of true activity to be calculated. As shown, 8 iterations can be considered a good choice in activity reconstruction for the largest spheres (Figure 3 a,b), but with subsets ≥8 instead of 4 as previously supposed. For the same subsets, but greater iterations, the same is also true for the third larger sphere (Figure 4c), while the PVE is clearly evident for the remaining spheres for all numbers of OSEM updates (Figure 4 d, e) considered.
The weighted fractional error has been calculated for each sphere as a function of the product of the subsets and iterations, i.e., EI, to estimate the error associated with the reconstruction algorithm. The results are shown in Figure 5, where the wRMSE (RMSE normalized to the true activity) is plotted as a function of EI. In this graph, data for each sphere refer to the highest weighting factor obtained by the OSEM updates considered in this study, that is EI=64, 80, 132 and 160. For a fixed choice of EI, the normalized wRMSE is sphere volume dependant because of the PVE reported in Figure 3. This is clearly visible for the two smaller spheres (wRMSE > 60%), starting from 64 EI and tend to decrease as the EI value increases.
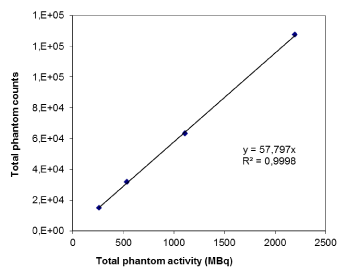
Figure 2. Dead time effect evaluation where total counts in the phantom is plotted against the real total activity injected in the phantom.
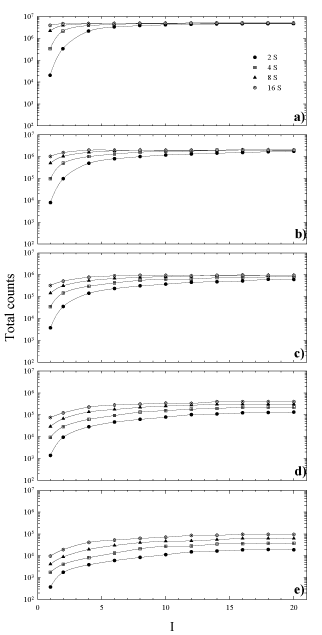
Figure 3. Total counts in each sphere versus the number of iterations for 4, 8 and 16 number of subsets. Sphere inner diameter: (a) 36mm, (b) 28mm, (c) 22mm, (d) 17mm, (e) 13mm.
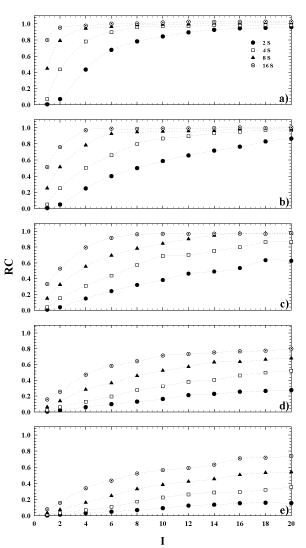
Figure 4. Recovery coefficient versus the number of iterations for 4, 8 and 16 number of subsets. Sphere inner diameter: (a) 36mm, (b) 28mm, (c) 22mm, (d) 17mm, (e) 13mm.
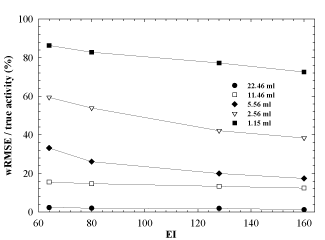
Figure 5. Weighted Root Mean Squared Error (wRMSE) normalized to the true activity as a function of equivalent iterations (EI).
Table 1. Resolution measurements performed with three hot capillary tubes (placed at the centre of the field of view, at a distance of 3cm and 6cm from the centre) filled with 177Lu and placed in a cylindrical phantom, filled with cold water. Spatial resolution estimations (mm), standard deviations (mm) and percentage noise are reported.
|
|
central |
3cm |
6cm |
4S4I |
average |
17,92 |
15,12 |
14,73 |
|
st. dev. |
0,02 |
0,11 |
0,26 |
|
noise% |
0,10 |
0,73 |
1,77 |
|
|
|
|
|
4S10I |
average |
13,44 |
11,40 |
10,97 |
|
st. dev. |
0,06 |
0,06 |
0,07 |
|
noise% |
0,44 |
0,53 |
0,61 |
|
|
|
|
|
4S18I |
average |
10,27 |
9,99 |
9,49 |
|
st. dev. |
0,16 |
0,07 |
0,19 |
|
noise% |
1,57 |
0,72 |
1,95 |
|
|
|
|
|
8S4I |
average |
12,87 |
11,73 |
11,39 |
|
st. dev. |
0,09 |
0,04 |
0,28 |
|
noise% |
0,67 |
0,32 |
2,47 |
|
|
|
|
|
8S10I |
average |
10,41 |
9,81 |
9,18 |
|
st. dev. |
0,75 |
0,46 |
1,10 |
|
noise% |
7,16 |
4,73 |
11,94 |
|
|
|
|
|
8S18I |
average |
9,73 |
8,55 |
8,27 |
|
st. dev. |
0,92 |
1,32 |
0,94 |
|
noise% |
9,48 |
15,43 |
11,39 |
|
|
|
|
|
16S4I |
average |
12,15 |
10,46 |
9,33 |
|
st. dev. |
0,47 |
0,92 |
0,40 |
|
noise% |
3,86 |
8,75 |
4,34 |
|
|
|
|
|
16S10I |
average |
8,94 |
8,50 |
8,01 |
|
st. dev. |
0,65 |
1,14 |
1,09 |
|
noise% |
7,29 |
13,42 |
13,58 |
|
|
|
|
|
16S18I |
average |
8,78 |
8,40 |
8,04 |
|
st. dev. |
0,60 |
1,41 |
1,40 |
|
2021 Copyright OAT. All rights reserv
noise% |
6,84 |
16,80 |
17,38 |
Discussion
The purpose of our work was to investigate the influence of the OSEM updates on 177Lu SPECT reconstruction and to quantify the error associated with the choice of OSEM parameters, as a function of the object volume with the PET NEMA IEC body phantom. The obtained results show that the choice of OSEM updates has great importance for the goal of activity quantification in SPECT for clinical purposes. It should be underlined that our study considers: 1) only spherical volumes; 2) the inserts were placed in fixed positions inside the phantom; 3) the inserts had similar distance from the SPECT/CT detectors; 4) the inserts were placed in a cold background. These choices are clearly distant from a clinical situation where organ motion and, consequently, unfixed lesion positions are present, together with background activity surrounding tissues responsible for the spill in effect. These assumptions are ideal and represent a simplification of the factors really affecting the loss of signal due to the PVE. However, they are essential in the investigation of their influence on the lesion activity quantification.
As reported in Table 1, while increasing the number of iterations for a fixed value of subsets, resolution improves, but noise increases too. The same is true if the iterations number is fixed, while subsets varying. From factory data sheet the resolution is 12.5 mm (at 10 cm distance, for medium energy collimators with 67Ga), but no information is provided about measurement method employed. Our results with the clinical radioisotope 177Lu show that our system resolution is better than what was reported in the factory data sheet for 67Ga and it shows a strong dependence on the chosen OSEM updates. The best measured spatial resolution values are achieved with the highest iteration and subset numbers (16 subsets and 18 iterations in our case). Indeed, the overall best spatial resolution (8 mm) can be obtained when spheres, or lesions in clinical cases, are nearest to detectors (6 cm from central position in our case). Generally, but this is principally dictated by time consuming analysis in a clinical contest, SPECT images are reconstructed with a fixed number of iterations and subsets, without considering the size and the location of the volume of interest.
Our results show that the appropriate OSEM update choice is important for two reasons: 1) for high number of updates even smaller spheres (diameter size down to tested resolution limit for a particular isotope) are detectable, in spite of a higher noise level in reconstructed images (about 17% for the overall best resolution of 8mm); 2) lesion detectability is as higher as the object is nearer to detector.
Therefore, the choice of a fixed number of iterations and subsets might be a drawback for dosimetric purpose. As shown in Figure 3, the choice of the same OSEM updates for different lesions could not be adequate in reaching the total count convergence inside the considered volume.
Objects of different spherical size don’t reach the convergence for any fixed number of OSEM updates, that is the choice for OSEM updates is object size dependent, and is related to the system spatial resolution. Hence, in a potential situation where patient lesions of different volume and different geometries are dealt with, the choice of using the same number of OSEM updates might be restrictive needing specific OSEM updates for smaller volumes. For volumes, larger than 5.5ml that is the volume of the median sphere (Figure 3 a-c), the number of subsets and iterations to be employed shouldn’t be less than 4 and 8, respectively.
Using the same choice of OSEM updates for VOIs smaller than5.5ml, such as the two smallest spheres in this study, the total counts convergence wouldn’t be reached because of the dominance of partial volume effect (Figure 3 d-e). Consequently, the estimation of the real activity in the object shall be influenced. In this situation, the quantification becomes anyway challenging and particularly critical because of the limited spatial resolution of SPECT modality. This is clear considering Figure 3, in terms of EI. For example, using a value of EI=64, this can be obtained using 8 subsets and 8 iterations, but also using 16 subsets and 4 iterations. From Figure 4, it can be seen that for these two possible combinations of the OSEM parameters, the bias of the RC relative to each VOI rises up while the volume of the sphere goes down. This, in turn, will cause a RC value reaching 1 for the biggest sphere, and be less than 1 for the smaller sphere at the same OSEM EI. A similar tendency was shown also in the work of Hippeläinen et al. [9]. That group performed a series of measurements of a phantom with a gamma camera of the same model of ours and with a similar acquisition and reconstruction protocol. However, they did not investigate the variation of response in function of the number of iterations and subsets. They only considered an EI given by 15 iterations and 16 subsets, investigating the influence of the compensation of attenuation only, scatter only and of both attenuation and scatter.
For this reason, our results show that smaller the sphere (hence, bigger the spread in total counts), bigger the error in activity estimation (Figure 5), ranging from 3.7% (biggest volume) to 35% (sphere volume of 5.56 ml) and 85% (smallest volume) at small values for subsets and iterations and from 3.7% (biggest volume) to 20% (sphere volume of 5.56 ml) and 79% (smallest volume) at higher values for subsets and iterations. Even if the EI quantity is very high, no additional gain for the wRMSE/ (true activity) ratio for spheres smaller than 4-5ml is detected.
Even a recent study [33] about the accuracy assessment of 177Lu quantification shows a similar increase of the signal in correspondence of high values of equivalent iterations and low filter size, as previously discussed. It was evaluated through the ratio between the activity quantified in a 22 mm sphere and the activity quantified in a 37 mm sphere. The approach adopted in the present study was more analytic and specifically referred to a series of differently sized spheres.
It should be noted that, if the lesion has an irregular shape, it may be unsafe to assume for the lesion the RC values for a volume equivalent sphere. In clinical cases, the activity quantification may be influenced by the organ motion and/or the patient breathing during data acquisition. Furthermore, it should not be forgotten that these RC curves are scanner specific (i.e., dependent on system spatial resolution, collimator, crystal thickness, source-to-detector distance, energy window settings, etc.), and similar experiments should be carried out on scanner from different vendors to derive analogous information in order to establish the best OSEM update choice.
The current study showed the need for PVE compensation to gain an accurate quantification of 177Lu for dosimetry purpose in a MRT trial focussed on lesions and organs dosimetry. This is particularly true when lesions or small organs should be drawn on SPECT images. A good compromise between spatial resolution, noise of the image and clinical reasons lead us to identify the EI value of 80 with 8 subsets and 10 iterations in abdomen exams, like the most appropriate in our 177Lu dosimetry trials.
Conclusion
The aim of the present work was to study the impact of OSEM algorithm settings in 177Lu SPECT/CT imaging for therapy dosimetry purposes. We evaluated the quantification accuracy of a specific choice of OSEM updates, as a function of the object volumes. A great dependence was observed on the number of iterations and subsets, particularly in relation to small volumes objects (volumes smaller than 5.5 ml).
The authors suggest to carefully optimize the reconstruction parameters of clinical cases in relation to the specific lesion size and shape. This is particularly true in SPECT imaging where a variety of functional studies, as well as different radioisotopes labelling the specific radiotracer used into the clinical practice, are present. Hence, physicians are recommended to adopt patient and lesion specific reconstruction parameters, in order to achieve a higher lesion detectability and a more accurate activity quantification both in diagnostics and therapeutics.
The approach of this paper could be successfully extended to other isotopes (i.e., 99mTc, 111In, 131I,…) with the aim to obtain more quantitatively accurate imaging in nuclear medicine studies.
The greatest authors’ interest is towards a quantification strongly related to dosimetry purposes in radionuclide therapy, which involve only some of the commonly used radionuclides. Among those it isn’t included the simple imaging isotope 99mTc, although it is considered a gold standard given its ideal single photopeak.
In perspective, it shall be interesting to apply the approach of this work to the more popular 99mTc imaging, giving a good indication of what the acquisition and reconstruction protocols are capable of under ideal imaging characteristics, which 177Lu certainly is not.
References
- Forrer F, Valkema R, Kwekkeboom DJ, de Jong M, Krenning EP (2007) Neuroendocrine tumors. Peptide receptor radionuclide therapy. Best Pract Res Clin Endocrinol Metab 21: 111-129. [Crossref]
- Kwekkeboom DJ, de Herder WW, Kam BL, van Eijk CH, van Essen M, et al. (2008) Treatment with the radiolabeled somatostatin analog [177 Lu-DOTA 0,Tyr3]octreotate: toxicity, efficacy, and survival. J Clin Oncol 2008: 26: 2124-2130. [Crossref]
- Strosberg J, El-Haddad G, Wolin E, Hendifar A, Yao J, et al. (2017) Phase 3 Trial of 177Lu-Dotatate for Midgut Neuroendocrine Tumors. N Engl J Med 376: 125-135. [Crossref]
- Ljungberg M, Celler A, Konijnenberg MW, Eckerman KF, Dewaraja YK, et al. (2016) MIRD Pamphlet No. 26: Joint EANM/MIRD Guidelines for Quantitative 177Lu SPECT Applied for Dosimetry of Radiopharmaceutical Therapy. J Nucl Med 57: 151-162. [Crossref]
- Sandström M, Garske U, Granberg D, Sundin A, Lundqvist H (2010) Individualized dosimetry in patients undergoing therapy with (177)Lu-DOTA-D-Phe (1)-Tyr (3)-octreotate. Eur J Nucl Med Mol Imaging 37: 212-225. [Crossref]
- Garkavij M, Nickel M, Sjögreen-Gleisner K, Ljungberg M, Ohlsson T, et al. (2010) 177Lu-[DOTA0,Tyr3] Octreotate therapy in patients with disseminated neuroendocrine tumors: analysis of dosimetry with impact on future therapeutic strategy. Cancer 116: 1084-1092. [Crossref]
- Janson ET, Sørbye H, Welin S, Federspiel B, Grønbaek H, et al. (2010) Nordic Guidelines 2010 for diagnosis and treatment of gastroenteropancreatic neuroendocrine tumours. Acta Oncol 49: 740-756. [Crossref]
- Uribe CF, Esquinas PL, et al. (2017) Accuracy of 177Lu activity quantification in SPECT imaging: a phantom study. EJNMMI Phys 4: 2. [Crossref]
- Hippeläinen E, Tenhunen M, Mäenpää H, Sohlberg A, et al. (2016) Quantitative accuracy of (177)Lu SPECT reconstruction using different compensation methods: phantom and patient studies. EJNMMI Res 6: 16. [Crossref]
- Ezziddin S1, Sabet A, Heinemann F, Yong-Hing CJ, Ahmadzadehfar H, et al. (2011) Response and Long-Term Control of Bone Metastases After Peptide Receptor Radionuclide Therapy with 177Lu-Octreotate. J Nucl Med 52: 1197-1203. [Crossref]
- Larsson E, Ljungberg M, Strand SE, Jönsson BA (2011) Monte Carlo calculations of absorbed doses in tumours using a modified MOBY mouse phantom for pre-clinical dosimetry studies. Acta Oncol 2011: 50: 973-980. [Crossref]
- Ljungberg M, Sjögreen-Gleisner K (2011) The accuracy of absorbed dose estimates in tumours determined by Quantitative SPECT: A Monte Carlo study. Acta Oncol 50: 981-989. [Crossref]
- Grozinsky-Glasberg S, Barak D, Fraenkel M, Walter MA, Müeller-Brand J, et al. (2011) Peptide receptor radioligand therapy is an effective treatment for the long-term stabilization of malignant gastrinomas. Cancer 117: 1377-1385. [Crossref]
- Ritt P, Vija H, Hornegger J, Kuwert T (2011) Absolute quantification in SPECT. Eur J Nucl Med Mol Imaging 38 Suppl 1: S69-77. [Crossref]
- Vandenberghe S, D'Asseler Y, Van de Walle R, Kauppinen T, Koole M, et al. (2001) Iterative reconstruction algorithms in nuclear medicine. Comput Med Imaging Graph 25: 105-111. [Crossref]
- Hudson HM1, Larkin RS (1994) Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans Med Imaging 13: 601-609. [Crossref]
- Liu S, Famcombe T (2007) Collimator-detector response compensation in quantitative SPECT reconstruction. IEEE Nucl Sci Symp Conf Rec 5: 3955-3960.
- Zingerman Y, Golan H, Moalem A (2009) Spatial linear recovery coefficients for quantitative evaluations in SPECT. Nucl Instr Meth Phy Res A 602: 607-613.
- Erlandsson K, Thomas B, Dickson J, Hutton BF (2011) Partial volume correction in SPECT reconstruction with OSEM. Nucl Instr Meth Phy Res A 2011: 648: S85-S88.
- Lyra M, Ploussi A (2011) Filtering in SPECT Image Reconstruction. Int J Biomed Imaging 2011: 693795. [Crossref]
- Willowson K, Bailey DL, Baldock C (2008) Quantitative SPECT reconstruction using CT-derived corrections. Phys Med Biol 53: 3099-3112. [Crossref]
- Zeintl J, Vija AH, Yahil A, Hornegger J, Kuwert T (2010) Quantitative accuracy of clinical 99mTc SPECT/CT using ordered subset expectation maximization with 3-dimensional resolution recovery, attenuation, and scatter correction. J Nucl Med 51: 921-928. [Crossref]
- Gustafsson J1, Brolin G, Cox M, Ljungberg M, Johansson L, et al. (2015) Uncertainty propagation for SPECT/CT-based renal dosimetry in (177)Lu peptide receptor radionuclide therapy. Phys Med Biol. 60: 8329-8346. [Crossref]
- D'Arienzo M, Cazzato M, Cozzella ML, Cox M, D'Andrea M, et al. (2016) Gamma camera calibration and validation for quantitative SPECT imaging with (177)Lu. Appl Radiat Isot 112: 156-164. [Crossref]
- Beauregard JM, Hofman MS, Pereira JM, Eu P, Hicks RJ (2011) Quantitative (177)Lu SPECT (QSPECT) imaging using a commercially available SPECT/CT system. Cancer Imaging 11: 56-66. [Crossref]
- Knoll P, Kotalova D, Köchle G, Kuzelka I, Minear G, et al. (2012) Comparison of advanced iterative reconstruction methods for SPECT/CT. Z Med Phys 22: 58-69. [Crossref]
- Dewaraja YK, Wilderman SJ, Ljungberg M, Koral KF, Zasadny K, et al. (2005) Accurate dosimetry in 131I radionuclide therapy using patient-specific, 3-dimensional methods for SPECT reconstruction and absorbed dose calculation. J Nucl Med 46: 840-849. [Crossref]
- Koral KF, Kritzmaan JN, Rogers VE, Ackermann RJ, Fessler JA. (2007) Optimizing the number of equivalent iterations of 3D OSEM in SPECT reconstruction of I-131 focal activities. Nucl Instr Meth Phys Res A 579: 326-329.
- Lassmann M, Chiesa C, Flux G, Bardiès M; EANM Dosimetry Committee (2011) EANM Dosimetry Committee guidance document: good practice of clinical dosimetry reporting. Eur J Nucl Med Mol Imaging 38: 192-200. [Crossref]
- Grassi E, Fioroni F, Ferri V, Mezzenga E, Sarti MA, et al. (2015) Quantitative comparison between the commercial software STRATOS(®) by Philips and a homemade software for voxel-dosimetry in radiopeptide therapy. Phys Med 31: 72-9. [Crossref]
- National Electrical Manufacturers Association (2007) Performance measurements of gamma camera. NEMA NU 1-2007. Rosslyn, VA.
- Kappadath SC (2011) Effects of voxel size and iterative reconstruction parameters on the spatial resolution of 99mTc SPECT/CT. J Appl Clin Med Phys 12: 3459. [Crossref]
- Marin G, Vanderlinden B, Karfis I, Guiot T, et al. (2017) Accuracy and precision assessment for activity quantification in individualized dosimetry of 177Lu-DOTATATE therapy. EJNMMI Phys 4: 7. [Crossref]


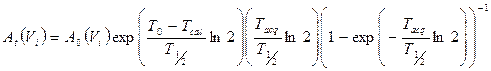 (3)
(3)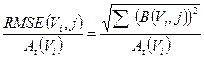 (4)
(4)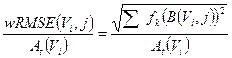 (6)
(6)


