In a previous part, I introduce the structured deformations theory (S.D.) by Del Piero & Owen restricting the attention on rescaled mono-dimensional sub-set. I find a particular solution in agree to the classical fracture models besides a response function in according either stress and strain fields distribution in biological materials. In this part we remark some concepts on S.D. theory, up-grading previous part and emphasizing the theory kernel, to follow on the classic bio-membrane elastic behavior until their damage and fracture under mechanical point of view. The question in first time is developed by the classical approach to denote the difficulty on macro and micro scale relationship besides their reciprocal influence over the deformation field. In fine I perform the S.D. implementation over a membrane model undergo to bending action, modelling in this way the ice needles actions, produced by freezing in cells preservation.
cell membrane, fracture energy, stress concentration, structured deformations
The consistent target in this paper is the introduction a size length and its relationship to sub-macroscopic geometrical change by the multiscale geometry of structured deformation. Particularly theory of elasticity with disarrangements linked with the first order S.D. allow the additive decomposition of the macroscopic deformation gradient in two distinct part, where one part is without disarrangement while the second part with disarrangement. What is relevant in this approach regard the upgrade of the nonlinear elasticity theory since the S.D. method is integrating voids formation and slip inside the theory. Performing the previous additive decomposition, this is without restriction on the size deformation, combining disarrangements as sub-macroscopic jump as approximating piecewise smooth deformation but, without gradient sub-macroscopic jump. To avoid all this setting a second-order structured deformation framework where, is posed, one other additive decomposition of the deformation gradient in a part without disarrangements and a part due to gradient disarrangements.
All this rest valid when large deformation appears in any material. The implementation of SD theory, as illustrated in the first part of this work, is centered on red blood cellular membrane during freezing and thawing occur in red blood cryopreservation. The physical questions which characterize this process, regard the ice needles formation and theirs mechanical contact with membrane surface. The roughness of the ice surface not allows a smooth contact with soft biological material but on the contrary, it appears a quasi-uniform distributed puncturing ice needle action. Generally the effects are dramatically ill-omened as well as generating the failures to a lot of red blood. The aim of this paper is to make an attempt besides genuine model, to simulate the mechanical effects on a biological and complex material which is the cellular membrane. The implementations of structured deformation theory, in my opinion, open a new way to consider strain at macroscale linked with strain at microscale. Particularly, in this specific question the S.D. tool allow us to differentiate the phospholipid deformation mechanism as first damaged element in the membrane global failure.
Remark on Structured Deformation Theory
Beginning from this section I recall the S.D. fundamentals by Del Piero & Owen which exhaustive reference are [1-5]. I select the crucial geometric elements needed to describe elasticity with disarrangements and for this I replay some important definition as:
Let W a regular subset of the Euclidean space 𝒮 and let 𝒰 the translation space of 𝒮. A structured deformation defined over 𝒮 is a pair (, 𝐺) which map:
𝑔: Ω↦ and: Ω↦𝒰 [1]
Such that 𝑔 is smooth, injective with smooth inverse; 𝐺 is continuous and the pair (𝑔,) respect the inequality:
0< c < det 𝐺(x) ⩽ det ∇𝑔(x) ∀x∈Ω [2]
Here in according to Del Piero & Owen [3] I will to remark the disarrangement concept as the term to describe non-smooth sub-macroscopic geometrical change likely slips or voids existing inside the elastic body. The term 𝐺 may be defined as deformation without disarrangements and as proved in theorem [5] the remarkable relations follow:
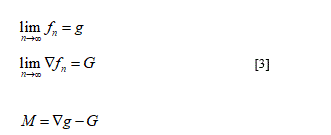
The deformations 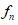 are called simple deformations and the pair (𝑔, 𝐺) is the structured deformations determined by the sequence
are called simple deformations and the pair (𝑔, 𝐺) is the structured deformations determined by the sequence  The tensor
The tensor  is the total deformation in x and 𝐺(x), 𝑀(x) are its elastic and inelastic part. From equation [3], the last formula representing a tensor value map defined as a deformation field due to disarrangements. So, becomes possible to define the additive decomposition:
is the total deformation in x and 𝐺(x), 𝑀(x) are its elastic and inelastic part. From equation [3], the last formula representing a tensor value map defined as a deformation field due to disarrangements. So, becomes possible to define the additive decomposition:
∇g = G + M
In other words the tensor field 𝐺 describe the limit deformation of the fracture-free parts of the body, while ∇g is the deformation observed at macroscale. Consequently, any macroscopic deformation can be explicit as sum of two parts: the first one without disarrangements and the second one with disarrangements. Concretely the S.D. theory takes care of materials governed by constitutive laws developing state variables. The newness in this theory may be individualized as state variables having geometrical characterization and, particularly, materials response is assumed to be elastic. All of this takes the theory as more adaptable to describe damaged materials and so different inelastic phenomena (plasticity, fracture, damage) can be viewed as singularities in the elastic state.
Bio membrane elastic properties
The bio-membrane constitutive behavior characterized of the elastic property of lipid bilayer find theirs elastic fundamentals from the Helfrich theory [6]. Based on the continuum mechanics theory it has proposed as first time, identifying three type of strain associated with the relatives stress and emphasizing the curvature role as equilibrium and stability parameter. Membrane curvature, have been investigated over a long time, by a lot of researcher in different fields as, biologists, medical, physician engineers, since the complex system has been stimulating to the different approach as interest. In fact in physic we usually want to reduce all the behavior to the fit formula while, in biology all details represent the foundation for life. The major interest to the membrane mechanical behavior is here represented by their curvature and remodeling [7]. According with the previous they are five ways to bend a cell membrane such that a positive or negative curvature is born. Particularly, more evident are changes in the lipid composition such to influence integral membrane proteins, cytoskeletal proteins and microtubule motor activity, scaffolding by peripheral membrane proteins and finally active helix insertion into membranes. Without loss generality here I focus my attention researching on already know mechanical model to up-grade and adequate theirs to structured deformation theory implementation. I find, other Helfrich various proposed model in classic literature as Tu et al. [8], Steigmann [9], Jenkis [10], Maleki et al. [11]. Unfortunately the approach used reproduce only macroscopic effects neglecting the fundamental size effects produced by the cell complex heterogeneity.
Similar results can be verified about failure model, Evans et al. [12] Fournier et al. [13] where in this last, the first order rupture line is found with increasing tension and a continuous increase in proto pore concentration with rising temperature till instability, emphasizing a possible failures mode of the lipid bilayer. Here remain as important fact to underline about failure some aspect derived by Helfrich model [6], where three types of strain, i.e. stretching, tilt and curvature are identified as well as likewise the associated stress. I will to point out the tilt bilayer model since the next first proposed model reproduces the relative deformation field. From now I will to deepen some aspects which content represent the framework under which create a coherent model implementing the S.D. theory. It’s my opinion that a logic way to the question is to individualize the macro-set such that the physical represent is more near to the real life. The first set may be represented by biological framework and so in according to Virga et al. [14] biological membranes are complex system since they consist of lipids, proteins and ions, water, carbohydrates the last three in minor amount. Between lipids there is a basic different among polar lipids like phospholipids and glycolipids, and non-polar lipids like sterols. Here help us underline that phospholipids are common in all membrane and again, their particular structure become binding to the intrinsic properties of the membrane. Lipid aggregates in the famed bilayer phase can further reduce to danger contact among aliphatic chains, water and ice by bending themselves to form vesicles. In particular in the Virga et al. paper [14] the membrane kinks have been exalted together tilt and curl-up phenomenon in phospholipids elements. All this will be a crucial element to consider in the next model formulation. About the mechanical and constitutive properties the biological membrane are elastics and this allow an efficient approach by variational methods. In according to Tan et al. [15] I impose some restrictions to the membrane behavior as:
i- The biological cells are assumed spherical and the internal intracellular liquid is assumed as hydrostatic pressure.
ii- the cellular membrane is composed of incompressible homogeneous isotropic material with constant thickness before the deformation.
iii- the cytoplasm is incompressible then the cell volume remain constant.
The previous sentences have been used in various continuum models representing again a valid base to suggest new model.
About the external action or interaction over the membrane this may be characterized through static and dynamic interactions. The dynamic is resulting from the destruction of the membrane fluctuations caused by embedded macromolecules, through rigid inclusion or specific receptors. The static interactions derived by perturbation of the bilayer structure or equilibrium membrane shape by the embedded or adsorbed macromolecules [16]. Finally in the next figures I bring the image of cell membrane freezing (Figure 1) and contemporarily reproduce the acceptable modeling of the red blood cell membrane together the possible deformation mode to the lipids elements (Figures 2 and 3) in according to the figure 1.
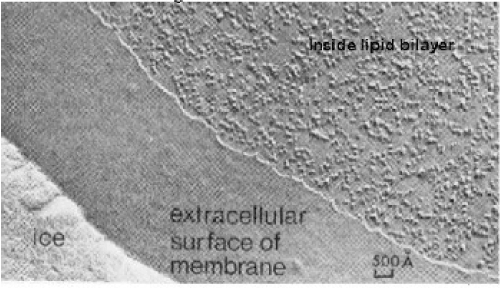
Figure 1. Freeze-fracture image (from cytochemistry.net)
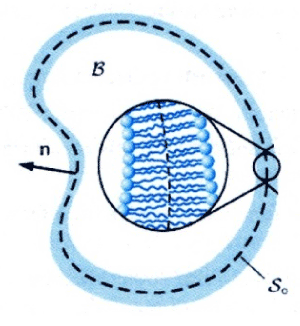
Figure 2. The defined bilayer micro-set
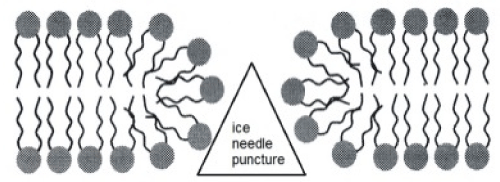
Figure 3. Kinematics of lipids failure
Classical approach
In according to Owen [5] classical measures of local deformation (for example, deformation gradient or plastic deformation) result as dimensionless. Nevertheless, in the continuum body, some geometrical change on the macroscopic and sub-macroscopic size can occur in some zones showing change in their boundary. In order to predict this phenomenon, elasticity and plasticity theories have been develop many tools as strain gradient, as well as, elastics or plastics deformations gradient types. Classically speaking to resolve our target, we need a procedure that allows the modelling microstructural size effects and this within the non-linear elasticity framework. Habitually one frequent tool is the gradient-enhanced computational homogenization procedure where is posed the macroscopic deformation gradient tensor and its gradient on a microstructural RVE. This approach, when stopped at first order, it may be based on the derivation of the local macroscopic constitutive behavior [17]. In this approach the deformation gradient has been derived by calculation on every point of the macrostructure and then using it to make the boundary conditions on the formulate RVE defined over a macroscopic point. Successively the macroscopic stress tensor derive by average the RVE stress field over the RVE volume. The final results under stress-strain law form, may be obtained
On this approach, generally, the resulting micro-deformation modes appear as macroscopically uniform, neglecting any bending local effects. All this since the scale length is negligible in comparison with microstructural length. The evident as well as salient result is that only simple first order deformation modes may be treated, omitting the bending mode in comparison to tension, compression and shear mode. This relevant and negative result affirm that the microstructure size can be considered as irrelevant and so localization phenomena cannot be taken in sufficient account. These results address us to expand high order theories, especially in homogenization approach, but their computational difficulty recommend all to see other as simplified way. In this contest, is my notice, that the structured deformation theory may be one convenient, as well as, innovative tool to resolve the questions.
Structured deformation implementation
From now I will to propose some different S.D. model applied to possible over know deformation mode on cellular membrane. I start with a first simple model reproducing, in an opportune subset the micro-deformation mode interesting membrane lipid bilayer when subjected by punch action (ice needle).
I consider a portion of the bilayer from strain zero state at shear deformation state after the contact ice membrane surface. The follow figures represent a reasonable deformation mode (classic shear mode) where the one single lipid slips respect to the next.
Considering a reference configuration N = 2 and let ℬ the continuum part under consideration having a rectangular form (0, L) x (0, h). Let the displacement field:
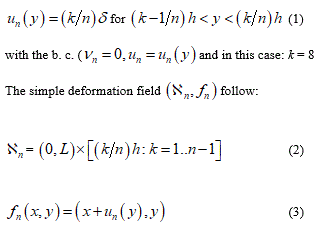
from this displacement its easy derive the gradient which value appear as
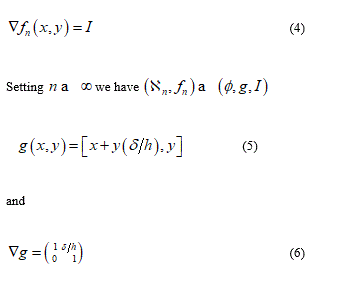
Consequently the previous formula confirms that the macro-deformation is a simple shear. Vice versa remembering the definition of tensor G we find G = I; namely, the disarrangements exist and the set of S.D. ( ∅, g , I ) may be descriptor of slips mode among single phospholipids constituents the bilayer. This micro-deformation framework appears without general plane deformation. To start a second implementation, I will before remark that usually the equality det G = det ∇g appears as satisfied but when it’s not and the inequality det G = det G < det ∇g follow, then it may be interpreted as incorporation of voids in the microstructure di a continuum elastic body. Another possible failure mechanics over the cellular membrane is represented by distinct micro-cracks namely rising of voids within the membrane surface. This phenomenon can be derived through different contact from fractal surface of the ice such that more needles are characterizing the contact surface.
For example consider a bi-dimensional set W where the body ℬ have the geometry by the set (0, L) x (0, L) and let
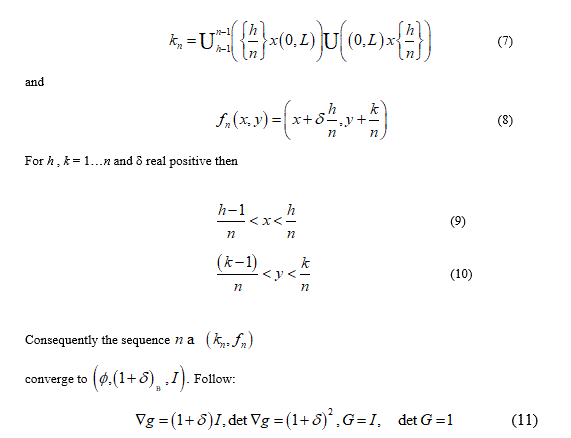
From the previous relationship we can to observe that 𝑑𝑒𝑡 𝐺 = 1 namely, no volume change without disarrangements. The change in volume from 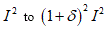 is due to the voids incorporation when to the limit
is due to the voids incorporation when to the limit  the body merge the various cut caused from the deformation effects (Figures 4-6).
the body merge the various cut caused from the deformation effects (Figures 4-6).
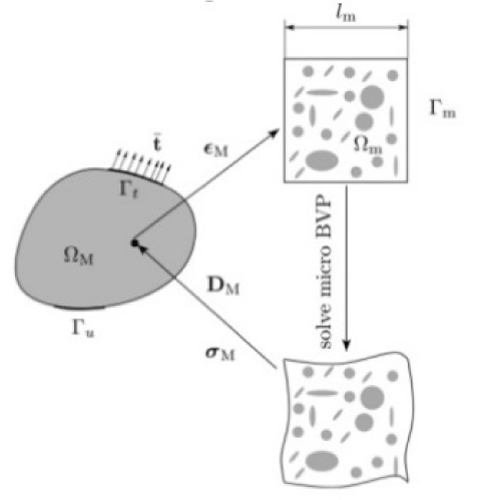
Figure 4. Gradient-enhanced computational homogenized scheme
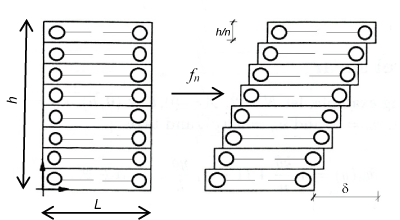
Figure 5. Shear deformation mode in phospholipid bilayer
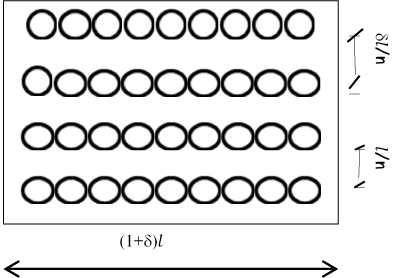
Figure 6. Voids generation after deformation
The proposed approach, explained through two classical damage and failure modes, has the asset to consider typical non-linear effects, as damage or failure, remaining in the linear elasticity computation and ever more hold great valuation the size effects. All this allow the better understanding to report the link micro-macro in complex as well as heterogeneous systems and materials. These first results consent a deep progression and invite us to develop model with addition of greater analytic support since, the linearity of the relationship, from which the 1^ order structured deformation theory, consent us to enrich both sequence and/or function, describing the different deformation modes in different size as in different constitutive relationship. Certainly the proposed models cannot be considered as exhaustive in fact, the next steps oblige us already to consider the case when the limitations of the S.D. theory result. Particularly when the term Ñ2g which role is to emphasize deformation affects a very small length scale, disappear. These penalties may be overcomes applying second-order structured deformation develop by Owen [5] as planned in a next paper.
- Del Piero G, Owen D R (1993) Structured deformations of continua. Archive for Rational Mechanics and Analysis 124: 99-155.
- Del Piero G (2001) On the energy of a structured deformations. Mathematics and Mechanics of Solids 6: 387-408.
- Del Piero G, Owen DR (Eds) (2004) Foundations of the theory of structured deformations. CISM Course and Lecture 447 Springer.
- Ambrosio L, Fusco N, Pallara D (2000) Functions of Bounded Variation and Free Discontinuity Problems, Clarendon Press Oxford.
- Owen DR (2017) Elasticity with Gradient-Disarrangements: A Multiscale Perspective for Strain-Gradient Theories of Elasticity and of Plasticity. Journal of Elasticity 127: 115-150
- Helfrich W (1973) Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforsch C 28: 693-703. [Crossref]
- McMahon HT, Gallop JL (2005) Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 438: 590-596. [Crossref]
- Tu ZC, An R, Ou-Yang ZC (2005): Elasticities and stabilities: lipid membranes vs cell membranes. ArXiv:q-bio/0501001v1 Cornell University library https.//ArVix.org.
- Steigmann DJ (2013) A well-posed finite strain model for thin elastic sheets with bending stiffness. Mathematics and Mechanics of Solids 18: 103-112
- Jenkins JT (1977) Static equilibrium configurations of a model red blood cell. J Math Biol 4: 149-169. [Crossref]
- Maleki M, Seguin B, Fried E (2013) Kinetics, materials symmetry, and energy densities for lipid bilayers with spontaneous curvature. Biomech Model Mechanobiol 12: 997-1017. [Crossref]
- Evans E, Smith BA (2011) Kinetics of Hole Nucleation in Biomembrane Rupture. New J Phys 13. [Crossref]
- Fournier L, Joós B (2003) Lattice model for the kinetics of rupture of fluid bilayer membranes. Phys Rev E Stat Nonlin Soft Matter Phys 67: 051908. [Crossref]
- Rosso R, Sonnet AM, Virga EG (2002) Dynamics of kinks in biological membrane. Continuum Mechanics and Thermodynamics 14: 127-136
- Tan Y, Sun D, Huang W, Cheng SH (2008) Mechanical modeling of biological cells in microinjection. IEEE Trans Nanobioscience 7: 257-266. [Crossref]
- Weiki TR (2003) Indirect interactions of membrane adsorbed cylinders. Eur Phys J E Soft Matter 12: 265-273. [Crossref]
- Kouznetsova V, Geers MGD, Brekelmans WAM (2002), Multi-scale constitutive modelling of heterogeneous materials with a gradient–enhanced computational homogenization scheme. Int. Journal for Numerical Methods in Engineering, 54: 1235-1260.
- Ji B, Gao H (2004): Mechanical properties of nanostructures of biological materials. Journal of the Mechanics and Physics of Solids 52: 1963-1990.

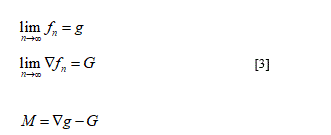
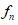 are called simple deformations and the pair (𝑔, 𝐺) is the structured deformations determined by the sequence
are called simple deformations and the pair (𝑔, 𝐺) is the structured deformations determined by the sequence 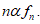 The tensor
The tensor 


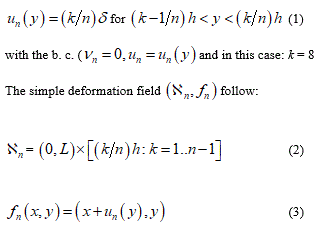
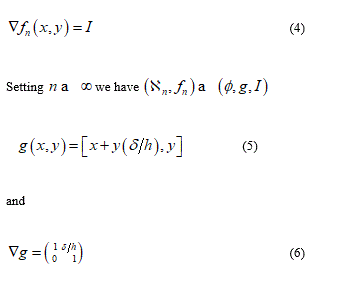
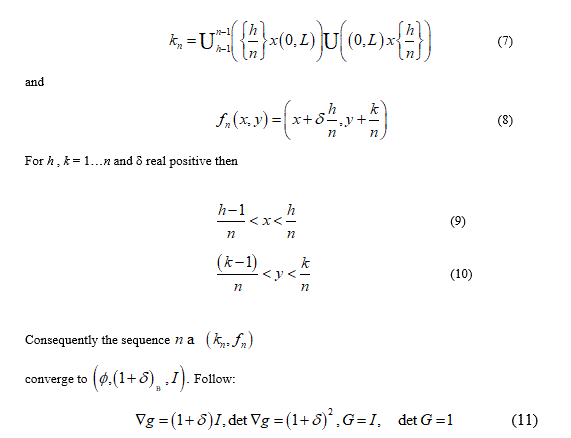
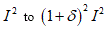 is due to the voids incorporation when to the limit
is due to the voids incorporation when to the limit 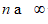 the body merge the various cut caused from the deformation effects (Figures 4-6).
the body merge the various cut caused from the deformation effects (Figures 4-6).

