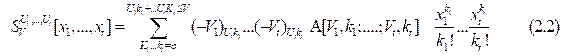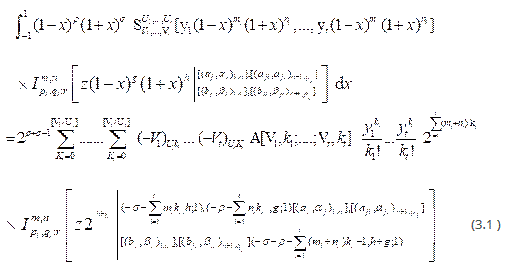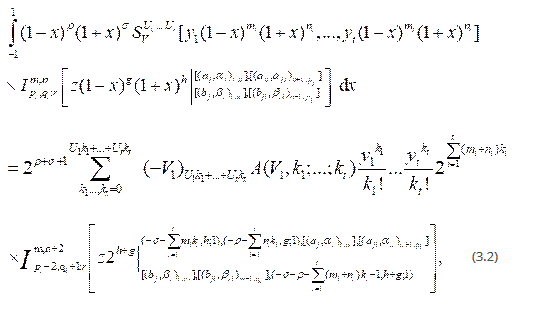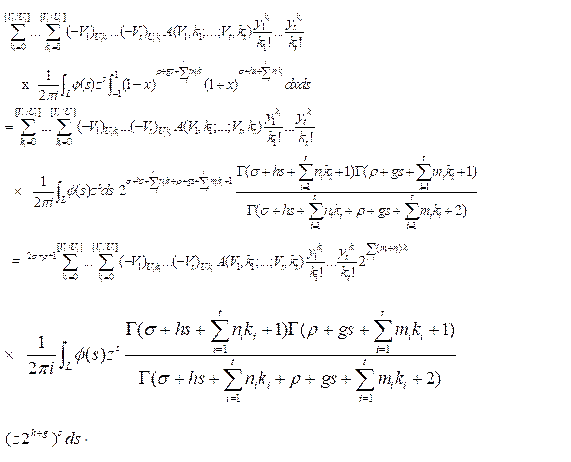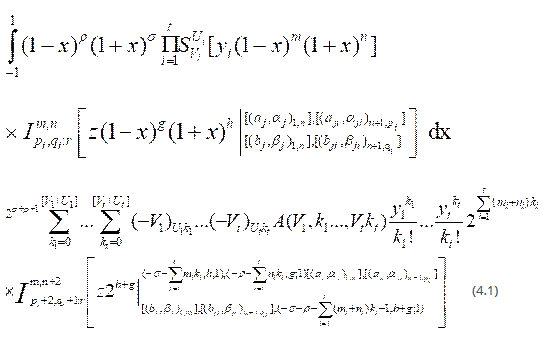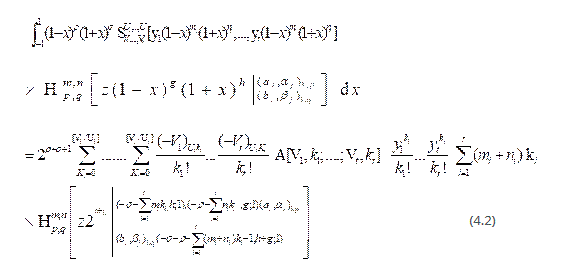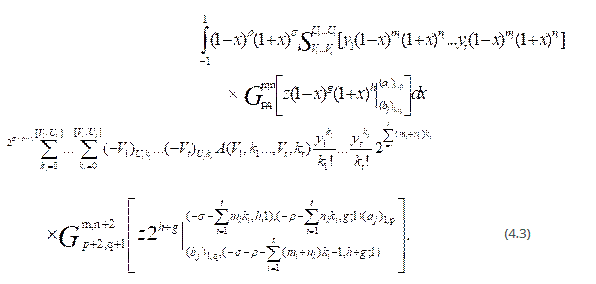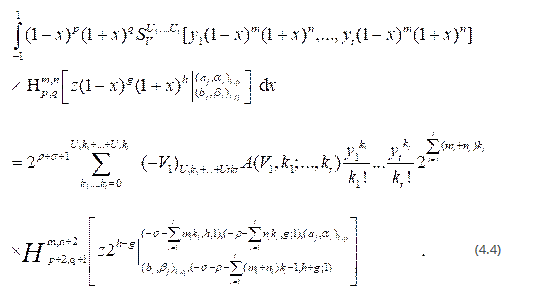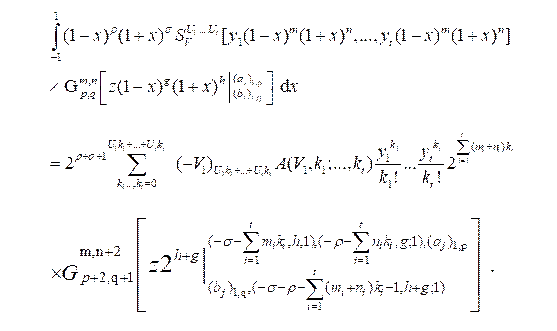This paper deals with some new integral relation of I- function of one variable.
I- function, multivariable polynomial
The I- function of one variable is defined by Saxena [1] and we shall represent here in the following manner:
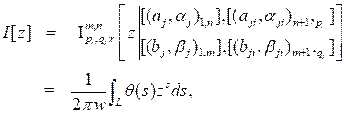 (1.1)
(1.1)
where  is a complex variable and
is a complex variable and
 (1.2)
(1.2)
In which log |z| represent the natural logarithm of |z| and arg |z| is not necessarily the principle value. An empty product is interpreted as unity, also,
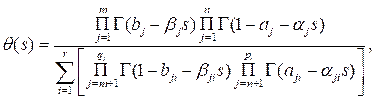 (1.3)
(1.3)
m, n and pi 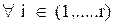 are non-negative integers satisfying 0 < n < pi, 0 < m < qi,
are non-negative integers satisfying 0 < n < pi, 0 < m < qi, 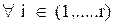 , αji, (j=1,….. pi; i = 1,………r) and βji (j = 1,….qi ; i = 1,….r) are assumed to be positive quantities for standardization purpose . Also aji ( j = 1,…., pi; i = 1,……,r) and bji ( j = 1,…….., qi; i = 1,…..,r) are complex numbers such that none of the points.
, αji, (j=1,….. pi; i = 1,………r) and βji (j = 1,….qi ; i = 1,….r) are assumed to be positive quantities for standardization purpose . Also aji ( j = 1,…., pi; i = 1,……,r) and bji ( j = 1,…….., qi; i = 1,…..,r) are complex numbers such that none of the points.
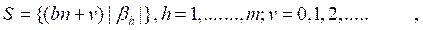 (1.4)
(1.4)
which are the poles of 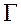 (bn – βnS), h = 1,……m and the points.
(bn – βnS), h = 1,……m and the points.
S =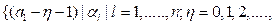 (1.5)
(1.5)
which are the poles of 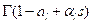 coincide with one another, i.e. with
coincide with one another, i.e. with
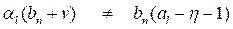 (1.6)
(1.6)
for n, h = 0, 1,2,….; h = 1,…., m; l = 1,…..,n.
Further, the contour L runs from -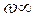 to +
to +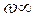 . Such that the poles of
. Such that the poles of 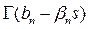 , h = 1……, m; lie to the right of L and the poles
, h = 1……, m; lie to the right of L and the poles 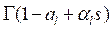 , l = 1,….,n lie to the left of L. The integral (1.1) converges, if |arg z| < ½ B π (B>0), A < 0, where
, l = 1,….,n lie to the left of L. The integral (1.1) converges, if |arg z| < ½ B π (B>0), A < 0, where
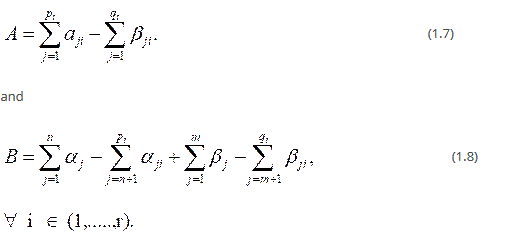
Gradshteyin and Ryzhik [2] given table of Integrals, series, Sharma [3] evaluated the integrals involving general class of polynomial with H-function, Srivastava and Garg [4] established some integrals involving a general class of polynomials and the multivariable H- function. Recently, Satyanarayana and Pragathi Kumar [5] has evaluated Some finite integrals involving multivariable polynomials, Agarwal [6] established integral involving the product of Srivastava’s polynomials and generalized Mellin-Barnes type of contour integral, Bhattar [7] established some integral formulas involving two  - function and multivariable’s general class of polynomiyals. Satyanarayana and Pragathi Kumar [5] has evaluated some finite integrals involving multivariable polynomials. Following them, I evaluated some new integrals involving multivariable polynomials, and I-function of one variable.
- function and multivariable’s general class of polynomiyals. Satyanarayana and Pragathi Kumar [5] has evaluated some finite integrals involving multivariable polynomials. Following them, I evaluated some new integrals involving multivariable polynomials, and I-function of one variable.
The following formulas will be required in our investigation
(i) The second class of multivariable polynomials given by Srivastava [8,9] is defined as follows:
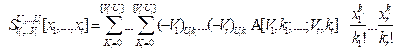 . (2.1)
. (2.1)
(ii) The first class of multivariable polynomials introduced by Srivastava and Garg [4] is defined as follows:
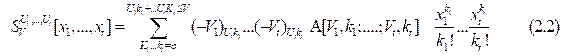
In this section we prove two integral formulae, which involving multivariable polynomials, and I function of one variable.
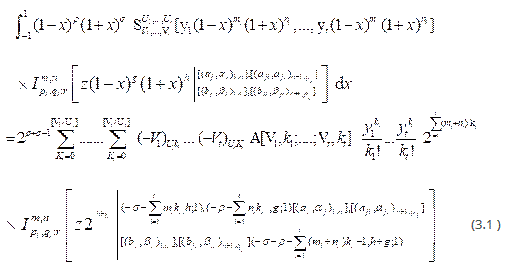
where mi>0 (i=1,…,t), ni>0 (i = 1,….,t) h ≥ 0 ,g ≥ 0 (not both are zero simultaneously).
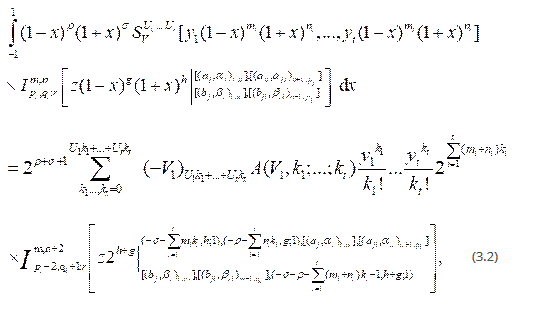
Provided the conditions stated in results (3.1) are satisfied.
Proof : To establish integral in (3.1), we express I-function occurring in its left –hand side interms of Mellin-Barnes [10] contour integral given by (3.1), the second class of polynomial given by (2.1). Then interchange the order of integration of summations and integration, we arrive the following:
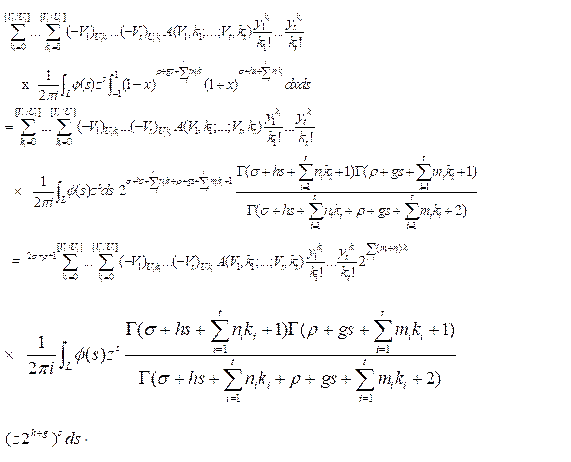
Now we evaluate the above integral with help of integral (2.2). Interpreting the resulting contour integral of H-function we can easily arrive at desired result (3.1).
To establish integral in (3.2) can be easily established on the same lines similar to the proof of (3.1).
Take A (V1,k1;…;Vt,kt) = A1(V1,k1)… At (Vt,kt) in (3.1) the multivariable polynomial 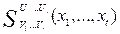 reduced to the product of well-known general class of polynomials
reduced to the product of well-known general class of polynomials 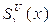 and the result (3.1) reduced to following form
and the result (3.1) reduced to following form
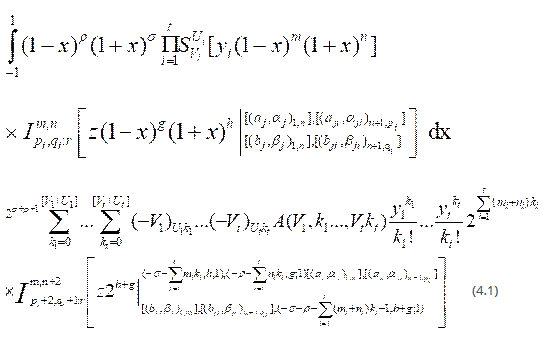
2021 Copyright OAT. All rights reserv
- Substituting r=1 in (3.1), we obtain :
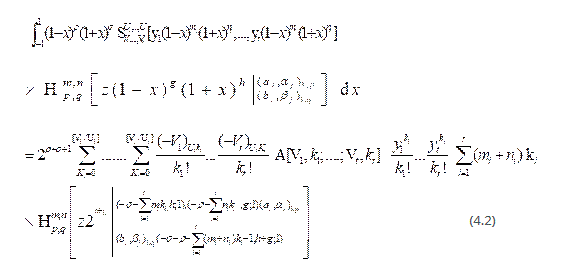
- Substituting αj=βj=1 in (4.2) we obtain
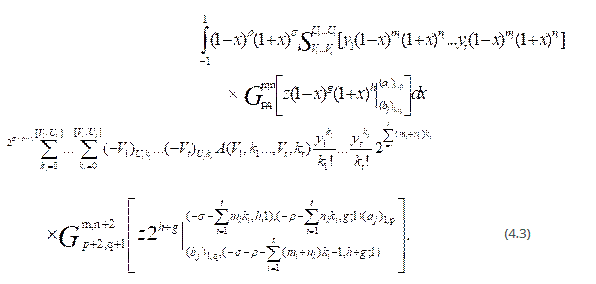
- Substituting r=1 in (3.2), we obtain :
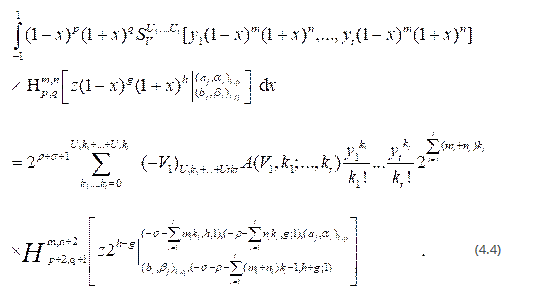
- Substituting αj=βj=1 in (4.4), we obtain
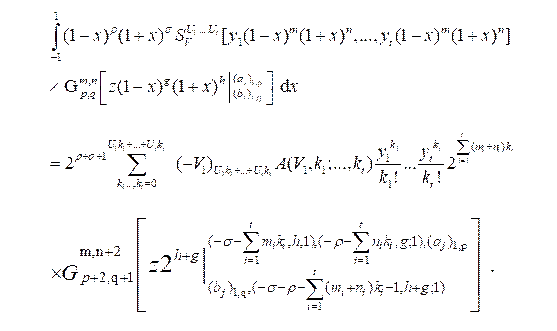
- Saxena S (1982) Formal solution of certain new pair of dual integral equations involving H-function. Proc Nat Acad Sci India 52, A. III, 366-375.
- Gradshteyin IS, Ryzhik IM (2001) Table of Integrals, series and products, 6/e. Academic press, New Delhi.
- Sharma RP (2006) On finite integrals involving Jacobi polynomials and the H-function. Kyungpook. Math J 46: 307-313.
- Srivastava HM, Garg M (1987) Some integrals involving a general class of polynomials and the multivariable H-function. Rev Roamaine Phys 32: 685-692.
- Satyanarayana B, Pragathi Kumar Y (2011) Some finite integrals involving multivariable polynomials, H-function of one variable and H-function of ‘r’ variables. African Journal of Mathematics and Computer Science Research 4: 281-285.
- Agarwal P (2012) On a unified integral involving the product of Srivastava’s polynomials and generalized Mellin-Barnes type of contour integral. Advances in Mechanical Engineering and its Applications (AMEA) 158: 2.
- Bhattar B (2014) Integral formulae’s involving two
 - function and multivariable’s general class of polynomiyals. ISCA Bushma.
- function and multivariable’s general class of polynomiyals. ISCA Bushma.
- Srivastava A (2010) The integration of certain products pertaining to the H-function with general polynomials. Ganita Sandesh 31/32: 51-58.
- Srivatsava HM, Singh NP (1983) The integration of certain products of the multivariable H-function with a general class of polynomials. Rend Circ Mat Palermo 32.
- Agarwal P, Chand M (2012) New theorems involving the generalized Mellin-Barnes type of contour integrals and general class of polynomials. GJSFRM 12.

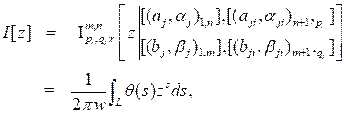 (1.1)
(1.1)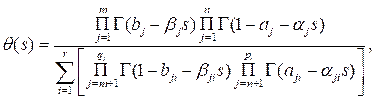 (1.3)
(1.3)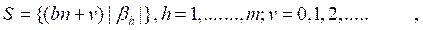 (1.4)
(1.4)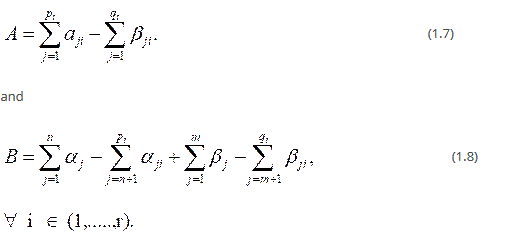
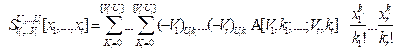 . (2.1)
. (2.1)